地址:http://poj.org/problem?id=2074
题目:
Line of Sight
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 4148 | Accepted: 1291 |
Description
An architect is very proud of his new home and wants to be sure it can be seen by people passing by his property line along the street. The property contains various trees, shrubs, hedges, and other obstructions that may block the view. For the purpose of this problem, model the house, property line, and obstructions as straight lines parallel to the x axis:
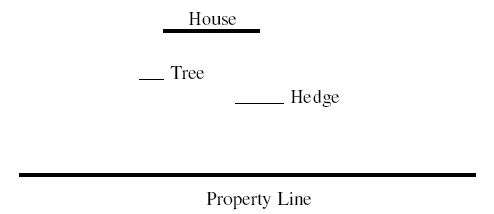
To satisfy the architect's need to know how visible the house is, you must write a program that accepts as input the locations of the house, property line, and surrounding obstructions and calculates the longest continuous portion of the property line from which the entire house can be seen, with no part blocked by any obstruction.

To satisfy the architect's need to know how visible the house is, you must write a program that accepts as input the locations of the house, property line, and surrounding obstructions and calculates the longest continuous portion of the property line from which the entire house can be seen, with no part blocked by any obstruction.
Input
Because each object is a line, it is represented in the input file with a left and right x coordinate followed by a single y coordinate:
< x1 > < x2 > < y >
Where x1, x2, and y are non-negative real numbers. x1 < x2
An input file can describe the architecture and landscape of multiple houses. For each house, the first line will have the coordinates of the house. The second line will contain the coordinates of the property line. The third line will have a single integer that represents the number of obstructions, and the following lines will have the coordinates of the obstructions, one per line.
Following the final house, a line "0 0 0" will end the file.
For each house, the house will be above the property line (house y > property line y). No obstruction will overlap with the house or property line, e.g. if obstacle y = house y, you are guaranteed the entire range obstacle[x1, x2] does not intersect with house[x1, x2].
< x1 > < x2 > < y >
Where x1, x2, and y are non-negative real numbers. x1 < x2
An input file can describe the architecture and landscape of multiple houses. For each house, the first line will have the coordinates of the house. The second line will contain the coordinates of the property line. The third line will have a single integer that represents the number of obstructions, and the following lines will have the coordinates of the obstructions, one per line.
Following the final house, a line "0 0 0" will end the file.
For each house, the house will be above the property line (house y > property line y). No obstruction will overlap with the house or property line, e.g. if obstacle y = house y, you are guaranteed the entire range obstacle[x1, x2] does not intersect with house[x1, x2].
Output
For each house, your program should print a line containing the length of the longest continuous segment of the property line from which the entire house can be to a precision of 2 decimal places. If there is no section of the property line where the entire house can be seen, print "No View".
Sample Input
2 6 6
0 15 0
3
1 2 1
3 4 1
12 13 1
1 5 5
0 10 0
1
0 15 1
0 0 0
Sample Output
8.80 No View
思路:首先排除掉不在house和proprety line的y的区间中线段,再求出对于每个线段的在property上的不可见区间。
如图所示:

然后把所有的区间按左端点为第一关键字,右端点为第二关键字从小到大排序,扫描一遍就好了。
1 /* 二维几何 */
2 /* 需要包含的头文件 */
3 #include<cstdio>
4 #include <cstring>
5 #include <cmath >
6 #include <iostream>
7 #include <algorithm>
8
9 using namespace std;
10 /** 常用的常量定义 **/
11 const double INF = 1e200;
12 const double eps = 1e-10;
13 const double PI = acos(-1.0);
14 const int Max = 1e5;
15 /** 基本几何结构 **/
16 struct Point
17 {
18 double x,y;
19 Point(double a=0, double b=0){x=a,y=b;}
20 bool operator<(const Point &ta)const
21 {
22 if(x==ta.x) return y<ta.y;
23 return x<ta.x;
24 }
25 friend Point operator+(const Point &ta,const Point &tb)
26 {
27 return Point(ta.x+tb.x,ta.y+tb.y);
28 }
29 friend Point operator-(const Point &ta,const Point &tb)
30 {
31 return Point(ta.x-tb.x,ta.y-tb.y);
32 }
33 };
34 struct Vec2D ///二维向量,*重载为点乘,/重载为叉乘
35 {
36 double x,y;
37 Vec2D(double ta,double tb){x=ta,y=tb;}
38 Vec2D(Point &ta){x=ta.x,y=ta.y;}
39 friend double operator*(const Vec2D &ta,const Vec2D &tb)
40 {
41 return ta.x*tb.x+ta.y*tb.y;
42 }
43 friend double operator/(const Vec2D &ta,const Vec2D &tb)
44 {
45 return ta.x*tb.y-ta.y*tb.x;
46 }
47 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb)
48 {
49 return Vec2D(ta.x+tb.x,ta.y+tb.y);
50 }
51 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb)
52 {
53 return Vec2D(ta.x-tb.x,ta.y-tb.y);
54 }
55 Vec2D operator=(const Vec2D &ta)
56 {
57 x=ta.x,y=ta.y;
58 return *this;
59 }
60 };
61 struct LineSeg ///线段,重载了/作为叉乘运算符,*作为点乘运算符
62 {
63 Point s,e;
64 LineSeg(){s=Point(0,0),e=Point(0,0);}
65 LineSeg(Point a, Point b){s=a,e=b;}
66 double lenth(void)
67 {
68 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y));
69 }
70 friend double operator*(const LineSeg &ta,const LineSeg &tb)
71 {
72 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y);
73 }
74 friend double operator/(const LineSeg &ta,const LineSeg &tb)
75 {
76 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x);
77 }
78 LineSeg operator=(const LineSeg &ta)
79 {
80 s=ta.s,e=ta.e;
81 return *this;
82 }
83 };
84 struct Line /// 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0
85 {
86 double a,b,c;
87 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;}
88 };
89
90 int sgn(double ta,double tb);
91 double fArea(Point &ta,Point &tb,Point &tc);
92 bool intersect(LineSeg &lx,LineSeg &ly);
93 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt);
94 double getdis(const Point &ta,const Point &tb);
95 bool cmp(const Point &ta,const Point &tb);
96 void graham(Point ps[],Point tb[],int n,int &num);
97 void ConvexClosure(Point ps[],Point tb[],int n,int &num);
98
99 void scf(LineSeg &lx)
100 {
101 cin>>lx.s.x>>lx.e.x>>lx.s.y;
102 lx.e.y=lx.s.y;
103 }
104 LineSeg hs,pl,cur,lx;
105 Point line[Max],tx,ty;
106 int main(void)
107 {
108 while(1)
109 {
110 int n,num=0;
111 scf(hs);
112 if(!(hs.s.x||hs.s.y||hs.e.x))
113 break;
114 scf(pl);
115 cin>>n;
116 for(int i=0;i<n;i++)
117 {
118 scf(cur);
119 if(sgn(cur.s.y,hs.s.y)<0&&sgn(cur.s.y,pl.s.y)>0)
120 {
121 lx=LineSeg(hs.s,cur.e);
122 intersection(lx,pl,tx);
123 lx=LineSeg(hs.e,cur.s);
124 intersection(lx,pl,ty);
125 if(tx.x>=ty.x)
126 line[num++]=Point(ty.x,tx.x);
127 else
128 line[num++]=Point(tx.x,ty.x);
129 }
130 }
131 sort(line,line+num);
132 double ans=0,rr=pl.s.x;
133 line[num++]=Point(pl.e.x,pl.e.x);
134 for(int i=0;i<num;i++)
135 if(!(line[i].y<pl.s.x || line[i].x>pl.e.x))
136 {
137 //printf("====%f %f
",line[i].x,line[i].y);
138 line[i].x=max(pl.s.x,line[i].x);
139 line[i].y=min(pl.e.x,line[i].y);
140 if(line[i].x>rr)
141 ans=max(ans,line[i].x-rr);
142 rr=max(line[i].y,rr);
143 }
144 if(sgn(ans,0))
145 printf("%.2f
",ans);
146 else
147 printf("No View
");
148
149 }
150
151 return 0;
152 }
153
154
155
156
157 /*******判断ta与tb的大小关系*******/
158 int sgn(double ta,double tb)
159 {
160 if(fabs(ta-tb)<eps)return 0;
161 if(ta<tb) return -1;
162 return 1;
163 }
164 /*********求两点的距离*************/
165 double getdis(const Point &ta,const Point &tb)
166 {
167 return sqrt((ta.x-tb.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y));
168 }
169 /************三角形面积**************************/
170 double fArea(Point &ta,Point &tb,Point &tc)
171 {
172 return fabs(LineSeg(ta,tb)/LineSeg(ta,tc)*0.5);
173 }
174
175 /*********** 判断P1P2是否和P3P4相交****************************
176 其中Pi坐标为(xi,yi),需要满足两个条件:
177 (1)快速排斥试验:
178 以P1P2为对角线的矩形S1是否和以P3P4为对角线的矩形S2相交,
179 即 min(x1,x2)<=max(x3,x4) && min(x3,x4)<=max(x1,x2)
180 && min(y1,y2)<=max(y3,y4) &&min(y3,y4)<=max(y1,y2)
181 (2)跨立试验:
182 点P1,P2必然在线段P3P4的不同侧,
183 点P3,P4必然在线段P1P2的不同侧,
184 ***************************************************************/
185 bool intersect(LineSeg &lx,LineSeg &ly)
186 {
187 return sgn(min(lx.s.x,lx.e.x),max(ly.s.x,ly.e.x))<=0
188 && sgn(min(ly.s.x,ly.e.x),max(lx.s.x,lx.e.x))<=0
189 && sgn(min(lx.s.y,lx.e.y),max(ly.s.y,ly.e.y))<=0
190 && sgn(min(ly.s.y,ly.e.y),max(lx.s.y,lx.e.y))<=0
191 && sgn((lx/LineSeg(lx.s,ly.s))*(lx/LineSeg(lx.s,ly.e)),0)<=0
192 && sgn((ly/LineSeg(ly.s,lx.s))*(ly/LineSeg(ly.s,lx.e)),0)<=0;
193 }
194 /************线段求交点**************************
195 返回-1代表直线平行,返回0代表直线重合,返回1代表线段相交
196 利用叉积求得点P分线段DC的比,
197 然后利用高中学习的定比分点坐标公式求得分点P的坐标
198 **************************************************/
199 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt)
200 {
201 pt=lx.s;
202 if(sgn(lx/ly,0)==0)
203 {
204 if(sgn(LineSeg(lx.s,ly.e)/ly,0)==0)
205 return 0;//重合
206 return -1;//平行
207 }
208 double t = (LineSeg(lx.s,ly.s)/ly)/(lx/ly);
209 pt.x+=(lx.e.x-lx.s.x)*t, pt.y+=(lx.e.y-lx.s.y)*t;
210 return 1;
211 }
212 /** ************凸包算法****************
213 寻找凸包的graham 扫描法
214 PS(PointSet)为输入的点集;
215 tb为输出的凸包上的点集,按照逆时针方向排列;
216 n为PointSet中的点的数目
217 num为输出的凸包上的点的个数
218 ****************************************** **/
219 bool cmp(const Point &ta,const Point &tb)/// 选取与最后一条确定边夹角最小的点,即余弦值最大者
220 {
221 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb);
222 // if(sgn(tmp,0)==0)
223 // return getdis(ps[0],ta)<getdis(ps[0],tb);
224 // else if(tmp>0)
225 // return 1;
226 return 0;
227 }
228 void graham(Point ps[],Point tb[],int n,int &num)
229 {
230 int cur=0,top=2;
231 for(int i=1;i<n;i++)
232 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
233 cur=i;
234 swap(ps[cur],ps[0]);
235 sort(ps+1,ps+n,cmp);
236 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2];
237 for(int i=3;i<n;i++)
238 {
239 while(sgn(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i]),0)<0)
240 top--;
241 tb[++top]=ps[i];
242 }
243 num=top+1;
244 }
245 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/
246 void ConvexClosure(Point ps[],Point tb[],int n,int &num)
247 {
248 LineSeg lx,ly;
249 int cur,ch;
250 bool vis[Max];
251 num=-1,cur=0;
252 memset(vis,0,sizeof(vis));
253 for(int i=1;i<n;i++)
254 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
255 cur=i;
256 tb[++num]=ps[cur];
257 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur];
258 /// 选取与最后一条确定边夹角最小的点,即余弦值最大者
259 while(1)
260 {
261 double mxcross=-2,midis,tmxcross;
262 ly.s=lx.e;
263 for(int i=0;i<n;i++)if(!vis[i])
264 {
265 ly.e=ps[i];
266 tmxcross=(lx*ly)/lx.lenth()/ly.lenth();
267 if(sgn(tmxcross,mxcross)>0 ||(sgn(tmxcross,mxcross)==0 && getdis(ly.s,ly.e)<midis))
268 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i;
269 }
270 if(ch==cur)break;
271 tb[++num]=ps[ch],vis[ch]=1;
272 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num];
273 }
274 }