地址:http://poj.org/problem?id=2826
题目:
An Easy Problem?!
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 13016 | Accepted: 2003 |
Description
It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width.
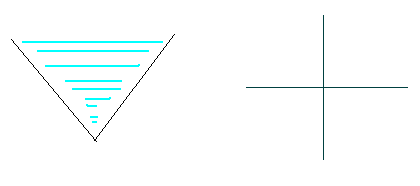
Your mission is to calculate how much rain these two boards can collect.

Your mission is to calculate how much rain these two boards can collect.
Input
The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x1, y1, x2, y2, x3, y3, x4, y4. (x1, y1), (x2, y2) are the endpoints of one board, and (x3, y3), (x4, y4) are the endpoints of the other one.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x1, y1, x2, y2, x3, y3, x4, y4. (x1, y1), (x2, y2) are the endpoints of one board, and (x3, y3), (x4, y4) are the endpoints of the other one.
Output
For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.
Sample Input
2
0 1 1 0
1 0 2 1
0 1 2 1
1 0 1 2
Sample Output
1.00 0.00
思路: 这题想还是好想,考虑到以下几种情况就可以啦。
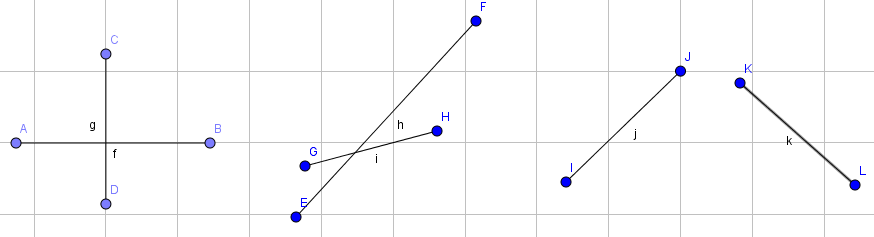
不过这傻逼题我还是玩了一天,把discuss里的所有数据都a了后还是wa!!!
因为求交点的模板错了!!!亏我还是从百度搜索求交点的页面的第一个网站上抄的模板!!!(坑人百度!!!)
还好机智的我在wa了一天后发现模板有问题,换了就ac了。
计算几何模板很重要!!!!!!!!!!!!
很重要!!!!!!!!
重要!!!!!!
因为一直wa的不能自理,所以写了两种思路的ac代码(其实差不多0.0)
1 /* 二维几何 */
2 /* 需要包含的头文件 */
3 #include <cstdio>
4 #include <cstring>
5 #include <cmath >
6 #include <iostream>
7 #include <algorithm>
8
9 using namespace std;
10 /** 常用的常量定义 **/
11 const double INF = 1e200;
12 const double eps = 1e-6;
13 const double PI = acos(-1.0);
14 const int Max = 1e6;
15
16 /** 基本几何结构 **/
17 struct Point
18 {
19 double x,y;
20 Point(double a=0, double b=0){x=a,y=b;}
21 bool operator<(const Point &ta)const
22 {
23 if(x==ta.x) return y<ta.y;
24 return x<ta.x;
25 }
26 friend Point operator+(const Point &ta,const Point &tb)
27 {
28 return Point(ta.x+tb.x,ta.y+tb.y);
29 }
30 friend Point operator-(const Point &ta,const Point &tb)
31 {
32 return Point(ta.x-tb.x,ta.y-tb.y);
33 }
34 };
35 struct Vec2D ///二维向量,*重载为点乘,/重载为叉乘
36 {
37 double x,y;
38 Vec2D(double ta,double tb){x=ta,y=tb;}
39 Vec2D(Point &ta){x=ta.x,y=ta.y;}
40 friend double operator*(const Vec2D &ta,const Vec2D &tb)
41 {
42 return ta.x*tb.x+ta.y*tb.y;
43 }
44 friend double operator/(const Vec2D &ta,const Vec2D &tb)
45 {
46 return ta.x*tb.y-ta.y*tb.x;
47 }
48 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb)
49 {
50 return Vec2D(ta.x+tb.x,ta.y+tb.y);
51 }
52 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb)
53 {
54 return Vec2D(ta.x-tb.x,ta.y-tb.y);
55 }
56 Vec2D operator=(const Vec2D &ta)
57 {
58 x=ta.x,y=ta.y;
59 return *this;
60 }
61 };
62 struct LineSeg ///线段,重载了/作为叉乘运算符,*作为点乘运算符
63 {
64 Point s,e;
65 LineSeg(){s=Point(0,0),e=Point(0,0);}
66 LineSeg(Point a, Point b){s=a,e=b;}
67 double lenth(void)
68 {
69 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y));
70 }
71 friend double operator*(const LineSeg &ta,const LineSeg &tb)
72 {
73 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y);
74 }
75 friend double operator/(const LineSeg &ta,const LineSeg &tb)
76 {
77 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x);
78 }
79 LineSeg operator=(const LineSeg &ta)
80 {
81 s=ta.s,e=ta.e;
82 return *this;
83 }
84 };
85 struct Line /// 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0
86 {
87 double a,b,c;
88 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;}
89 };
90
91
92 int sgn(double ta,double tb);
93 double getdis(const Point &ta,const Point &tb);
94 double fArea(Point &ta,Point &tb,Point &tc);
95 bool intersect(LineSeg &lx,LineSeg &ly);
96 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt);
97 bool cmp(const Point &ta,const Point &tb);
98 void graham(Point ps[],Point tb[],int n,int &num);
99 void ConvexClosure(Point ps[],Point tb[],int n,int &num);
100
101
102
103 int main(void)
104 {
105 int n;
106 double ans;
107 Point cs1,cs2;
108 LineSeg lx,ly,lz;
109 cin>>n;
110 while(n--)
111 {
112 ans=0;
113 cin>>lx.s.x>>lx.s.y>>lx.e.x>>lx.e.y;
114 cin>>ly.s.x>>ly.s.y>>ly.e.x>>ly.e.y;
115 if(lx.s.y>lx.e.y)
116 swap(lx.s,lx.e);
117 if(ly.s.y>ly.e.y)
118 swap(ly.s,ly.e);
119 //判断两条直线斜率,是否相交,是否重合或平行
120 if(sgn(lx.s.y,lx.e.y)&&sgn(ly.s.y,ly.e.y)&&intersect(lx,ly)&&intersection(lx,ly,cs1)==1)
121 {
122 lz=LineSeg(ly.e,Point(ly.e.x,1e5));
123 if(sgn(getdis(lx.e,cs1),getdis(ly.e,cs1))>=0 && intersect(lz,lx))
124 {
125 printf("0.00
");
126 continue;
127 }
128 lz=LineSeg(lx.e,Point(lx.e.x,1e5));
129 if(sgn(getdis(lx.e,cs1),getdis(ly.e,cs1))<0 && intersect(lz,ly))
130 {
131 printf("0.00
");
132 continue;
133 }
134 lz=LineSeg(Point(0,0),Point(1,0));
135 if(sgn(lz*lx/lx.lenth(),lz*ly/ly.lenth())<0)
136 swap(lx,ly);
137 if(lx.e.y>=ly.e.y)
138 {
139 lz=LineSeg(ly.e,Point(lx.e.x,ly.e.y));
140 intersection(lx,lz,cs2);
141 ans=fArea(cs1,cs2,ly.e);
142 }
143 else
144 {
145 lz=LineSeg(lx.e,Point(ly.e.x,lx.e.y));
146 intersection(ly,lz,cs2);
147 ans=fArea(cs1,cs2,lx.e);
148 }
149
150 }
151 printf("%.2f
",ans+eps);
152
153 }
154
155 return 0;
156 }
157
158
159
160
161
162 /*******判断ta与tb的大小关系*******/
163 int sgn(double ta,double tb)
164 {
165 if(fabs(ta-tb)<eps)return 0;
166 if(ta<tb) return -1;
167 return 1;
168 }
169 /*********求两点的距离*************/
170 double getdis(const Point &ta,const Point &tb)
171 {
172 return sqrt((ta.x-tb.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y));
173 }
174 /************三角形面积**************************/
175 double fArea(Point &ta,Point &tb,Point &tc)
176 {
177 return fabs(LineSeg(ta,tb)/LineSeg(ta,tc)*0.5);
178 }
179
180 /*********** 判断P1P2是否和P3P4相交****************************
181 其中Pi坐标为(xi,yi),需要满足两个条件:
182 (1)快速排斥试验:
183 以P1P2为对角线的矩形S1是否和以P3P4为对角线的矩形S2相交,
184 即 min(x1,x2)<=max(x3,x4) && min(x3,x4)<=max(x1,x2)
185 && min(y1,y2)<=max(y3,y4) &&min(y3,y4)<=max(y1,y2)
186 (2)跨立试验:
187 点P1,P2必然在线段P3P4的不同侧,
188 点P3,P4必然在线段P1P2的不同侧,
189 ***************************************************************/
190 bool intersect(LineSeg &lx,LineSeg &ly)
191 {
192 return sgn(min(lx.s.x,lx.e.x),max(ly.s.x,ly.e.x))<=0
193 && sgn(min(ly.s.x,ly.e.x),max(lx.s.x,lx.e.x))<=0
194 && sgn(min(lx.s.y,lx.e.y),max(ly.s.y,ly.e.y))<=0
195 && sgn(min(ly.s.y,ly.e.y),max(lx.s.y,lx.e.y))<=0
196 && sgn((lx/LineSeg(lx.s,ly.s))*(lx/LineSeg(lx.s,ly.e)),0)<=0
197 && sgn((ly/LineSeg(ly.s,lx.s))*(ly/LineSeg(ly.s,lx.e)),0)<=0;
198 }
199 /************线段求交点**************************
200 返回-1代表直线平行,返回0代表直线重合,返回1代表线段相交
201 利用叉积求得点P分线段DC的比,
202 然后利用高中学习的定比分点坐标公式求得分点P的坐标
203 **************************************************/
204 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt)
205 {
206 pt=lx.s;
207 if(sgn(lx/ly,0)==0)
208 {
209 if(sgn(LineSeg(lx.s,ly.e)/ly,0)==0)
210 return 0;//重合
211 return -1;//平行
212 }
213 double t = (LineSeg(lx.s,ly.s)/ly)/(lx/ly);
214 pt.x+=(lx.e.x-lx.s.x)*t, pt.y+=(lx.e.y-lx.s.y)*t;
215 return 1;
216 }
217 /** ************凸包算法****************
218 寻找凸包的graham 扫描法
219 PS(PointSet)为输入的点集;
220 tb为输出的凸包上的点集,按照逆时针方向排列;
221 n为PointSet中的点的数目
222 num为输出的凸包上的点的个数
223 ****************************************** **/
224 bool cmp(const Point &ta,const Point &tb)/// 选取与最后一条确定边夹角最小的点,即余弦值最大者
225 {
226 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb);
227 // if(sgn(tmp,0)==0)
228 // return getdis(ps[0],ta)<getdis(ps[0],tb);
229 // else if(tmp>0)
230 // return 1;
231 return 0;
232 }
233 void graham(Point ps[],Point tb[],int n,int &num)
234 {
235 int cur=0,top=2;
236 for(int i=1;i<n;i++)
237 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
238 cur=i;
239 swap(ps[cur],ps[0]);
240 sort(ps+1,ps+n,cmp);
241 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2];
242 for(int i=3;i<n;i++)
243 {
244 while(sgn(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i]),0)<0)
245 top--;
246 tb[++top]=ps[i];
247 }
248 num=top+1;
249 }
250 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/
251 void ConvexClosure(Point ps[],Point tb[],int n,int &num)
252 {
253 LineSeg lx,ly;
254 int cur,ch;
255 bool vis[Max];
256 num=-1,cur=0;
257 memset(vis,0,sizeof(vis));
258 for(int i=1;i<n;i++)
259 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
260 cur=i;
261 tb[++num]=ps[cur];
262 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur];
263 /// 选取与最后一条确定边夹角最小的点,即余弦值最大者
264 while(1)
265 {
266 double mxcross=-2,midis,tmxcross;
267 ly.s=lx.e;
268 for(int i=0;i<n;i++)if(!vis[i])
269 {
270 ly.e=ps[i];
271 tmxcross=(lx*ly)/lx.lenth()/ly.lenth();
272 if(sgn(tmxcross,mxcross)>0 ||(sgn(tmxcross,mxcross)==0 && getdis(ly.s,ly.e)<midis))
273 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i;
274 }
275 if(ch==cur)break;
276 tb[++num]=ps[ch],vis[ch]=1;
277 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num];
278 }
279 }
第二种:
1 /* 二维几何 */
2 /* 需要包含的头文件 */
3 #include <cstdio>
4 #include <cstring>
5 #include <cmath >
6 #include <iostream>
7 #include <algorithm>
8
9 using namespace std;
10 /** 常用的常量定义 **/
11 const double INF = 1e200;
12 const double eps = 1e-6;
13 const double PI = acos(-1.0);
14 const int Max = 1e6;
15
16 /** 基本几何结构 **/
17 struct Point
18 {
19 double x,y;
20 Point(double a=0, double b=0){x=a,y=b;}
21 bool operator<(const Point &ta)const
22 {
23 if(x==ta.x) return y<ta.y;
24 return x<ta.x;
25 }
26 friend Point operator+(const Point &ta,const Point &tb)
27 {
28 return Point(ta.x+tb.x,ta.y+tb.y);
29 }
30 friend Point operator-(const Point &ta,const Point &tb)
31 {
32 return Point(ta.x-tb.x,ta.y-tb.y);
33 }
34 };
35 struct Vec2D ///二维向量,*重载为点乘,/重载为叉乘
36 {
37 double x,y;
38 Vec2D(double ta,double tb){x=ta,y=tb;}
39 Vec2D(Point &ta){x=ta.x,y=ta.y;}
40 friend double operator*(const Vec2D &ta,const Vec2D &tb)
41 {
42 return ta.x*tb.x+ta.y*tb.y;
43 }
44 friend double operator/(const Vec2D &ta,const Vec2D &tb)
45 {
46 return ta.x*tb.y-ta.y*tb.x;
47 }
48 friend Vec2D operator+(const Vec2D &ta,const Vec2D &tb)
49 {
50 return Vec2D(ta.x+tb.x,ta.y+tb.y);
51 }
52 friend Vec2D operator-(const Vec2D &ta,const Vec2D &tb)
53 {
54 return Vec2D(ta.x-tb.x,ta.y-tb.y);
55 }
56 Vec2D operator=(const Vec2D &ta)
57 {
58 x=ta.x,y=ta.y;
59 return *this;
60 }
61 };
62 struct LineSeg ///线段,重载了/作为叉乘运算符,*作为点乘运算符
63 {
64 Point s,e;
65 LineSeg(){s=Point(0,0),e=Point(0,0);}
66 LineSeg(Point a, Point b){s=a,e=b;}
67 double lenth(void)
68 {
69 return sqrt((s.x-e.x)*(s.x-e.x)+(s.y-e.y)*(s.y-e.y));
70 }
71 friend double operator*(const LineSeg &ta,const LineSeg &tb)
72 {
73 return (ta.e.x-ta.s.x)*(tb.e.x-tb.s.x)+(ta.e.y-ta.s.y)*(tb.e.y-tb.s.y);
74 }
75 friend double operator/(const LineSeg &ta,const LineSeg &tb)
76 {
77 return (ta.e.x-ta.s.x)*(tb.e.y-tb.s.y)-(ta.e.y-ta.s.y)*(tb.e.x-tb.s.x);
78 }
79 LineSeg operator=(const LineSeg &ta)
80 {
81 s=ta.s,e=ta.e;
82 return *this;
83 }
84 };
85 struct Line /// 直线的解析方程 a*x+b*y+c=0 为统一表示,约定 a >= 0
86 {
87 double a,b,c;
88 Line(double d1=1, double d2=-1, double d3=0){ a=d1,b=d2,c=d3;}
89 };
90
91
92 int sgn(double ta,double tb);
93 double getdis(const Point &ta,const Point &tb);
94 double fArea(Point &ta,Point &tb,Point &tc);
95 bool intersect(LineSeg &lx,LineSeg &ly);
96 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt);
97 bool cmp(const Point &ta,const Point &tb);
98 void graham(Point ps[],Point tb[],int n,int &num);
99 void ConvexClosure(Point ps[],Point tb[],int n,int &num);
100
101
102
103 int main(void)
104 {
105 int n;
106 double ans;
107 Point cs1,cs2;
108 LineSeg lx,ly,lz;
109 cin>>n;
110 while(n--)
111 {
112 ans=0;
113 cin>>lx.s.x>>lx.s.y>>lx.e.x>>lx.e.y;
114 cin>>ly.s.x>>ly.s.y>>ly.e.x>>ly.e.y;
115 if(lx.s.y>lx.e.y)
116 swap(lx.s,lx.e);
117 if(ly.s.y>ly.e.y)
118 swap(ly.s,ly.e);
119 lz=LineSeg(Point(-1,0),Point(0,0));
120 if(sgn(lx.s.y,lx.e.y)&&sgn(ly.s.y,ly.e.y)&&intersect(lx,ly)&&intersection(lx,ly,cs1))
121 {
122 if(sgn(lz*lx/lx.lenth(),lz*ly/ly.lenth())<0)
123 swap(lx,ly);
124 if( (sgn(lx.e.x,cs1.x)>=0 && sgn(ly.e.x,cs1.x)>=0 && sgn(ly.e.x,lx.e.x)<0)
125 || (sgn(lx.e.x,cs1.x)<=0 && sgn(ly.e.x,cs1.x)<=0 && sgn(lx.e.x,ly.e.x)>0)
126 || (sgn(lx.e.x,cs1.x)>=0 && sgn(ly.e.x,cs1.x)<=0))
127 {
128 if(lx.e.y>=ly.e.y)
129 {
130 lz=LineSeg(ly.e,Point(lx.e.x,ly.e.y));
131 intersection(lx,lz,cs2);
132 ans=fArea(cs1,cs2,ly.e);
133 }
134 else
135 {
136 lz=LineSeg(lx.e,Point(ly.e.x,lx.e.y));
137 intersection(ly,lz,cs2);
138 ans=fArea(cs1,cs2,lx.e);
139 }
140 }
141 }
142 printf("%.2f
",ans+eps);
143
144 }
145
146 return 0;
147 }
148
149
150
151
152
153 /*******判断ta与tb的大小关系*******/
154 int sgn(double ta,double tb)
155 {
156 if(fabs(ta-tb)<eps)return 0;
157 if(ta<tb) return -1;
158 return 1;
159 }
160 /*********求两点的距离*************/
161 double getdis(const Point &ta,const Point &tb)
162 {
163 return sqrt((ta.x-tb.x)*(ta.x-tb.x)+(ta.y-tb.y)*(ta.y-tb.y));
164 }
165 /************三角形面积**************************/
166 double fArea(Point &ta,Point &tb,Point &tc)
167 {
168 return fabs(LineSeg(ta,tb)/LineSeg(ta,tc)*0.5);
169 }
170
171 /*********** 判断P1P2是否和P3P4相交****************************
172 其中Pi坐标为(xi,yi),需要满足两个条件:
173 (1)快速排斥试验:
174 以P1P2为对角线的矩形S1是否和以P3P4为对角线的矩形S2相交,
175 即 min(x1,x2)<=max(x3,x4) && min(x3,x4)<=max(x1,x2)
176 && min(y1,y2)<=max(y3,y4) &&min(y3,y4)<=max(y1,y2)
177 (2)跨立试验:
178 点P1,P2必然在线段P3P4的不同侧,
179 点P3,P4必然在线段P1P2的不同侧,
180 ***************************************************************/
181 bool intersect(LineSeg &lx,LineSeg &ly)
182 {
183 return sgn(min(lx.s.x,lx.e.x),max(ly.s.x,ly.e.x))<=0
184 && sgn(min(ly.s.x,ly.e.x),max(lx.s.x,lx.e.x))<=0
185 && sgn(min(lx.s.y,lx.e.y),max(ly.s.y,ly.e.y))<=0
186 && sgn(min(ly.s.y,ly.e.y),max(lx.s.y,lx.e.y))<=0
187 && sgn((lx/LineSeg(lx.s,ly.s))*(lx/LineSeg(lx.s,ly.e)),0)<=0
188 && sgn((ly/LineSeg(ly.s,lx.s))*(ly/LineSeg(ly.s,lx.e)),0)<=0;
189 }
190 /************线段求交点**************************
191 返回-1代表直线平行,返回0代表直线重合,返回1代表线段相交
192 利用叉积求得点P分线段DC的比,
193 然后利用高中学习的定比分点坐标公式求得分点P的坐标
194 **************************************************/
195 bool intersection(LineSeg &lx,LineSeg &ly,Point &pt)
196 {
197 pt=lx.s;
198 if(sgn(lx/ly,0)==0)
199 {
200 if(sgn(LineSeg(lx.s,ly.e)/ly,0)==0)
201 return 0;//重合
202 return -1;//平行
203 }
204 double t = (LineSeg(lx.s,ly.s)/ly)/(lx/ly);
205 pt.x+=(lx.e.x-lx.s.x)*t, pt.y+=(lx.e.y-lx.s.y)*t;
206 return 1;
207 }
208 /** ************凸包算法****************
209 寻找凸包的graham 扫描法
210 PS(PointSet)为输入的点集;
211 tb为输出的凸包上的点集,按照逆时针方向排列;
212 n为PointSet中的点的数目
213 num为输出的凸包上的点的个数
214 ****************************************** **/
215 bool cmp(const Point &ta,const Point &tb)/// 选取与最后一条确定边夹角最小的点,即余弦值最大者
216 {
217 // double tmp=LineSeg(ps[0],ta)/LineSeg(ps[0],tb);
218 // if(sgn(tmp,0)==0)
219 // return getdis(ps[0],ta)<getdis(ps[0],tb);
220 // else if(tmp>0)
221 // return 1;
222 return 0;
223 }
224 void graham(Point ps[],Point tb[],int n,int &num)
225 {
226 int cur=0,top=2;
227 for(int i=1;i<n;i++)
228 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
229 cur=i;
230 swap(ps[cur],ps[0]);
231 sort(ps+1,ps+n,cmp);
232 tb[0]=ps[0],tb[1]=ps[1],tb[2]=ps[2];
233 for(int i=3;i<n;i++)
234 {
235 while(sgn(LineSeg(tb[top-1],tb[top])/LineSeg(tb[top-1],ps[i]),0)<0)
236 top--;
237 tb[++top]=ps[i];
238 }
239 num=top+1;
240 }
241 /** 卷包裹法求点集凸壳,参数说明同graham算法 **/
242 void ConvexClosure(Point ps[],Point tb[],int n,int &num)
243 {
244 LineSeg lx,ly;
245 int cur,ch;
246 bool vis[Max];
247 num=-1,cur=0;
248 memset(vis,0,sizeof(vis));
249 for(int i=1;i<n;i++)
250 if(sgn(ps[cur].y,ps[i].y)>0 || (sgn(ps[cur].y,ps[i].y)==0 && sgn(ps[cur].x,ps[i].x)>0))
251 cur=i;
252 tb[++num]=ps[cur];
253 lx.s=Point(ps[cur].x-1,ps[cur].y),lx.e=ps[cur];
254 /// 选取与最后一条确定边夹角最小的点,即余弦值最大者
255 while(1)
256 {
257 double mxcross=-2,midis,tmxcross;
258 ly.s=lx.e;
259 for(int i=0;i<n;i++)if(!vis[i])
260 {
261 ly.e=ps[i];
262 tmxcross=(lx*ly)/lx.lenth()/ly.lenth();
263 if(sgn(tmxcross,mxcross)>0 ||(sgn(tmxcross,mxcross)==0 && getdis(ly.s,ly.e)<midis))
264 mxcross=tmxcross,midis=getdis(ly.s,ly.e),ch=i;
265 }
266 if(ch==cur)break;
267 tb[++num]=ps[ch],vis[ch]=1;
268 lx.s=tb[num-1],lx.e=tb[num],ly.s=tb[num];
269 }
270 }