对于"从一组数中挑出最大的K个数"这个在面试中经常会遇到,所以这次好好的去解析它,而当拿到这个问题时第一时间能想到解法就是:先对数据进行排序,然后再取最大的K个元素,当然这思路没毛病,但是对于数据量非常大(如:一万个数)的情况是不是先对它进行排序的代价太高了,有木有比较优的解法呢?当然有,那就是采用上篇学习到的利用二叉堆排序去解决。
定义二叉堆结构:
首先是需要用代码去实现一个堆这样的数据结构,而堆的特性在上篇【http://www.cnblogs.com/webor2006/p/7685197.html】中已经有介绍了,下面直接实现,先定义框架:
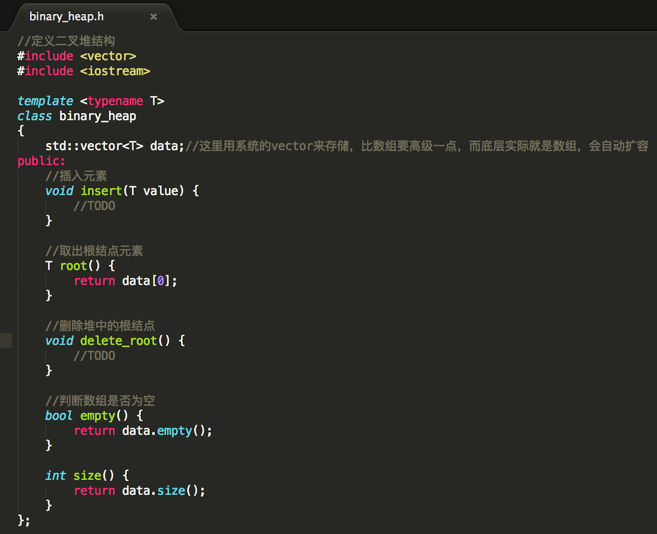
其中核心就是实现数据的插入和删除,这个整个思想已经在之前介绍堆时介绍过了,这里就不多阐述了,下面来分别实现:
①、insert():插入元素
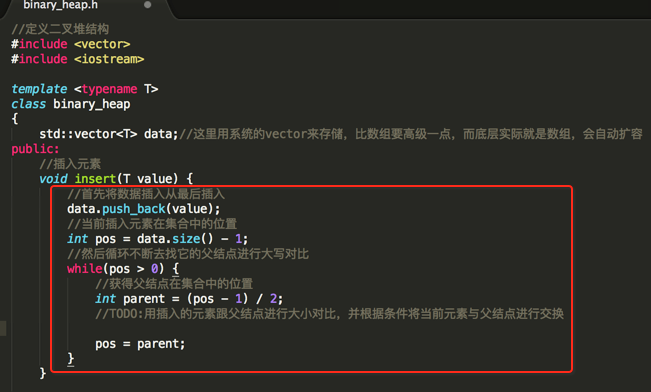
其中怎么根据当前结点得到它的父结点的公式是:int parent = (pos - 1) / 2;猭由是根据父节点可以计算得到它左右子节点的位置,公式如:

上面公式是在上篇对堆的理论上有详细说明,而其中的i就是父元素的位置,所以其推导过程,拿左子节点为例:
因为:子节点位置 = 2 * 父结点位置 + 1
所以:父结点位置parent = (子节点位置pos - 1) / 2
接下来实现关键的对比部份,由于堆有小堆跟大堆,如下:
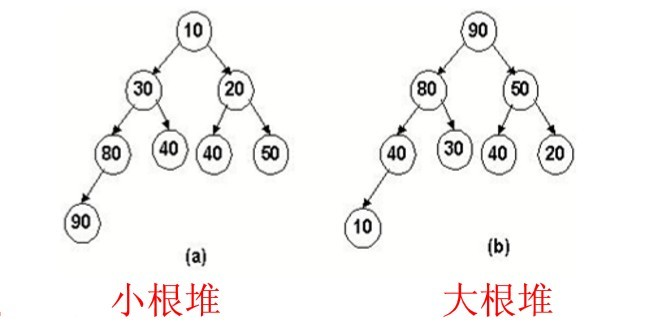
所以这个结构为了考虑到这两种情况,将对比的情况写成抽象方法,由具体大小堆的类去实现这个对比条件,如下:
//定义二叉堆结构 #include <vector> #include <iostream> #include <algorithm> //for swap template <typename T> class binary_heap { std::vector<T> data;//这里用系统的vector来存储,比数组要高级一点,而底层实际就是数组,会自动扩容 protected: virtual bool compare(T a, T b) = 0;//定义虚方法,具体实现由子类决定 public: //插入元素 void insert(T value) { //首先将数据插入从最后插入 data.push_back(value); //当前插入元素在集合中的位置 int pos = data.size() - 1; //然后循环不断去找它的父结点进行大写对比 while(pos > 0) { //获得父结点在集合中的位置 int parent = (pos - 1) / 2; //用插入的元素跟父结点进行大小对比,并根据条件将当前元素与父结点进行交换 if(parent < 0 || !compare(value, data[parent])) { //退出循环条件:如果parent如果小于0则代表遍历结束了;如果对比条件不满足【大堆是当前值小于父结点、小堆是当前值大于父结点】 break; } //说明需要进行数据交换,采用系统库中的现有函数去做既可 std::swap(data[pos], data[parent]); pos = parent; } } //取出根结点元素 T root() { return data[0]; } //删除堆中的根结点 void delete_root() { //TODO } //判断数组是否为空 bool empty() { return data.empty(); } int size() { return data.size(); } }; template <typename T> class max_binary_heap : public binary_heap<T> { protected: virtual bool compare(T a, T b) { return a > b; } }; template <typename T> class min_binary_heap : public binary_heap<T> { protected: virtual bool compare(T a, T b) { return a < b; } };
这里为了能看出整个插入的一个排序结果,所以在完成排序之后,将当前元素输出出来:
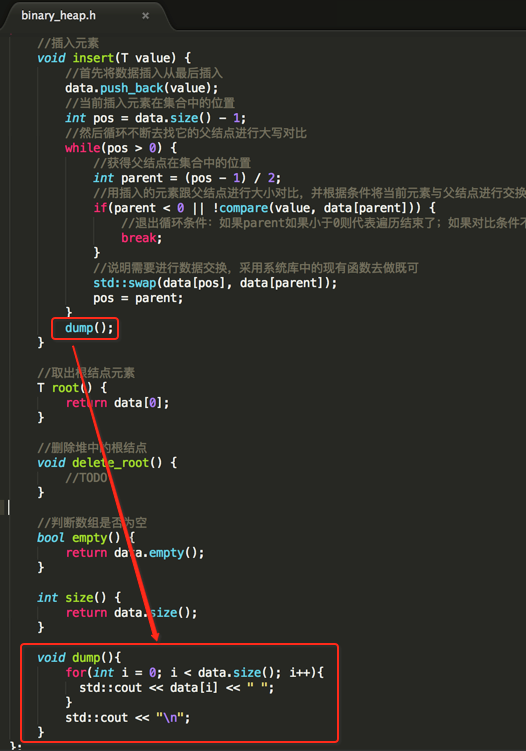
这就是整个的往堆中插入元素的方法,因为比较容易理解这里就不debug啦~
②、delete_root():删除根结点
接着得实现第二个核心方法:从堆中删除根结点,这个在上篇的理论中了将整个删除的过程做了一个详细的阐述,所以这里直接按着其思路来实现它:

接着拿左右子结点跟当前要删除的结点找出最大的数,如图:

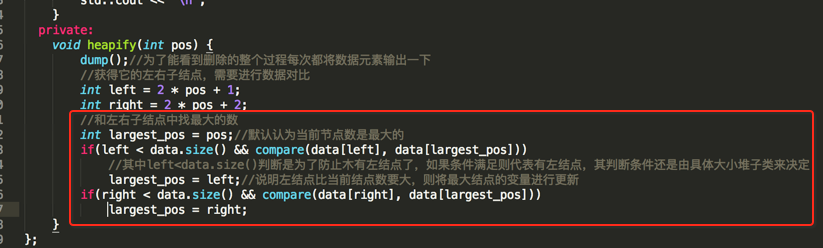
然后拿当前节点跟最大数进行对比,如果当前节点就是最大数则啥都不做递归结束,如果当前节点跟最大数不一样则进行数据交换如下:

至上,整个二叉堆数据结构就已经实现啦,具体如何去使用继续往下看。
完成堆排序:
上面已经定义好了二叉堆的数据结构了,接着来用它完成关键的二叉堆的排序,如下:

具体如何实现呢?有了二叉堆的数据结构了其实非常简单,首先先将待排序的数组元素都插入到堆中【这里用最大堆为例】:

编译运行:
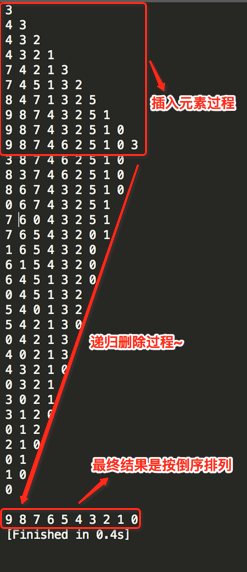
如果想升序排列其实很简单,将最大堆换成最小堆既可,如下:
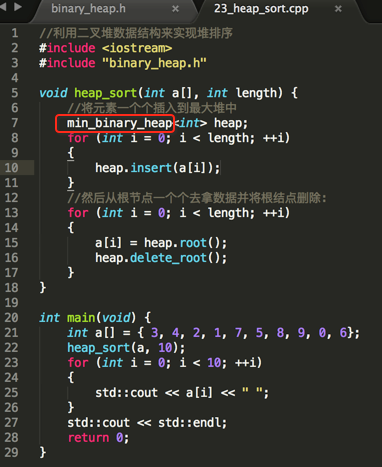
编译运行:
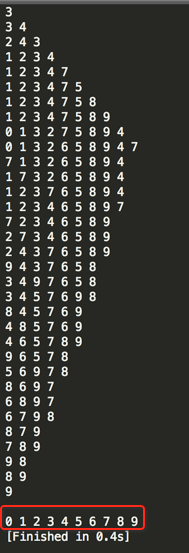
实现拿最大K元素:
堆排序已经实现了,最后就到了这次的主题啦,怎么从大量数据集中拿最大的K个元素呢?
先搭建框架:
思考:是用最小堆还是最大堆去实现?
假如采用最大堆去实现,因为它的根结点永远是最大的,那先将元素都插入到最大堆中,然后拿出k个根结点元素那不就是取出最大的k个元素啦,思路很正点,但是!!!在拿元素之前得先把元素中的所有元素都插入到堆中才行,假如有100万个数,那不这个最大堆的大小就得是100万这个大写,效率貌似不高,所以可以考虑用最小堆试试。
假如采用最小堆,那可以先将前K个元素插入到最小堆中,然后再依次去跟K之外的元素一一跟根结点进行对比,如果比根结点要大则将根结点删除,将这个较大的数插入到最小堆中,也就是!!!永远堆中的数据个数只有K个,而不像最大堆那样堆需要N个元素的大小,这样用最小堆去实现优越感顺间就提升了,所以!这里采用最小堆来实现。
具体如下:

编译运行:
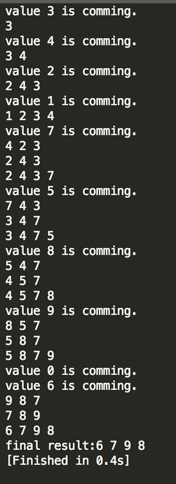
这样就成功找到了最大的K元素啦~
时间复杂度分析:

所以说这里用最小堆实现的时间复杂度是T(n) = O(n * logk),其中n就是总元数个数,k则是要筛选的K个元素。
但是如果用最大堆实现的话其复杂度就变成了O(n * log n)了,因为循环里面最坏的情况就得进行log n次对比,其中n肯定是比要比k要大得多,所以说用最小堆实现的算法是比较优的。
而如果用最原始通过双层循环的方式来实现:最外层是k次循环,而最里层是n次循环,一个个元素进行大小比较,那这样的时间复杂度就是O(k * n)了,很明显这性能是最差的,虽说实现起来是最容易的。