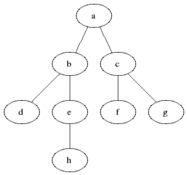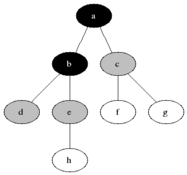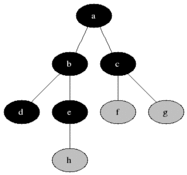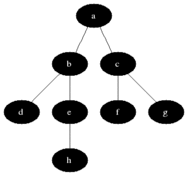
之前学过利用递归实现BFS二叉树搜索(http://www.cnblogs.com/webor2006/p/7262773.html),这次学习利用队列(Queue)来实现,关于什么时BFS这里不多说了,先贴张图来直观回忆下:
实现一个队列【采用数组实现】:
这时同样采用模版技术可以往队列中去放任何类型的数据,而这个队列同样是声明在头文件中,以便在需要用到队列的地方去随时包含它,下面先来定个初步框架:
/** * 利用数组来实现队列 */ template <typename T> class queue { T* data;//用数组来实现队列 int head/* 头指向的位置 */, tail/* 尾指向的位置 */, size/* 当前队列存放的元素个数 */, data_length/* 总队列的大小 */; public: queue(int length):head(0), tail(0), size(0), data_length(length) { data = new T[length]; } //入队列 void push(T value) { } //出队列 void pop() { } //取出队列最早的元素 T top() { } //判断队列是否为空 bool isEmpty() { } };
具体实现如下:
/** * 利用数组来实现队列 */ template <typename T> class queue { T* data;//用数组来实现队列 int head/* 头指向的位置 */, tail/* 尾指向的位置 */, size/* 当前队列存放的元素个数 */, data_length/* 总队列的大小 */; public: queue(int length):head(0), tail(0), size(0), data_length(length) { data = new T[length]; } //入队列 void push(T value) { if(size == data_length) { throw "queue is full";//如果队列已经满了则直接抛异常,实际可以去将数组扩容,这里简单处理,重在学习数据结构 } data[head] = value; head = (head + 1) % data_length;//这是为了循环利用,如果队列还有空间的话 size++; } //出队列 void pop() { if(isEmpty()) { throw "queue is empty"; } tail = (tail + 1) % data_length;//这是为了循环利用 size--; } //取出队列最早的元素 T top() { if(isEmpty()) throw "You cannot get the top element from an empty queue"; return data[tail]; } //判断队列是否为空 bool isEmpty() { return size == 0; } };
这里先来使用一下它,看入队跟出队的结果是否如预期:
编译运行:

对于上面的写法下面用图来将其整个过程画出来:
①、
创建一个大小为3的队列,其中head、tail指向数组0的位置,其中目前是一个size=0空数组

②、
往队列中插入元素1:
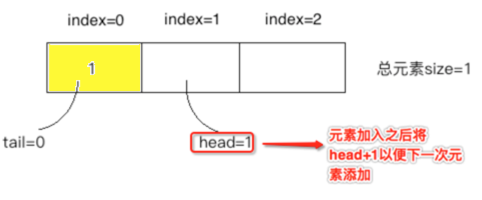
③、
往队列中插入元素2:
④、
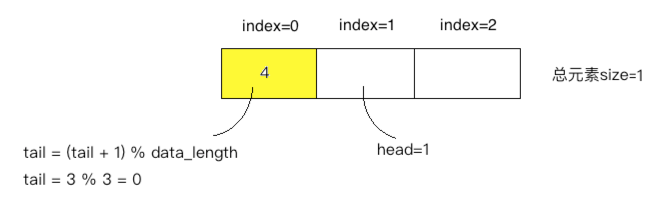
往队列中插入元素3,这里需要注意啦!!!head会循环利用,指向数组0的位置:

⑤、
根据队列先进先出的原则拿最早放入的元素也就是tail所指向的元素:

⑥、
根据队列先进先出的原则拿最早放入的元素也就是tail所指向的元素:
⑦、
根据队列先进先出的原则拿最早放入的元素也就是tail所指向的元素:
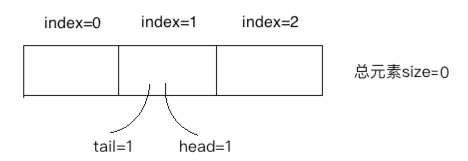
这时注意啦!!!tail跟head一样也会循环利用,又回到index=0的位置了:

⑧、
由于此时size=0了,所以会打印出"queue is empty"。
⑨、
⑩、
⑪、
由于此时size=0了,所以会打印出"queue is empty"。
总结:
1、添加元素放到head处,添加完成之后将head+1以便下次进行存放。
2、拿元素时是从tail处拿,拿完之后也是将tail+1以便拿下一个元素,因为是先进先出原则。
基于上节的实现来利用队列实现二叉树的BFS遍历:
先贴一下上节的代码,基于这个二叉树利用队列去实现:
#include <iostream> #include "stack.h" #include "queue.h" //用来表示二叉树 struct treenode{ int data; treenode* left;//左结点 treenode* right;//右结点 treenode(int value):data(value), left(nullptr), right(nullptr){} }; //前序遍历 void pre_order(treenode* root){ Stack<treenode*> stack;//声明一个栈 treenode* current_node = root; while(current_node) { //1、首先打印当前结点,因为是前序遍历 std::cout << current_node->data << std::endl; //2、如果存在右结点则将其入栈暂存,待左结点输出完之后再去处理这些右结点 if(current_node->right) stack.push(current_node->right); //3、不断去处理左结点,直到左结点处理完了,则从栈中拿右点进行处理 if(current_node->left)//如果有左结点,则将它做为当前处理的结点不断输出 current_node = current_node->left; else { //这时左结点已经处理完了 if(stack.isEmpty())//如果缓存栈已经为空了则说明整个二叉树的遍历结束了 current_node = nullptr; else { //则取出栈顶的右结点进行处理,由于是后进先出,所以拿出来的永远是最新插入的右结点 current_node = stack.top(); stack.pop();//将其元素从栈顶弹出 } } } } //利用队列实现BFS void level_order(treenode* root){ //TODO } int main(void) { //构建二叉树: //1、第一层根结点 treenode* root = new treenode(5); //2、第二层结点 root->left = new treenode(3); root->right = new treenode(8); //3、第三层结点 root->left->left = new treenode(1); root->left->right = new treenode(4); root->right->left = new treenode(7); //4、第四层结点 root->right->left->left = new treenode(6); pre_order(root); std::cout << "##################" << std::endl; level_order(root); return 0; }
其二叉树为: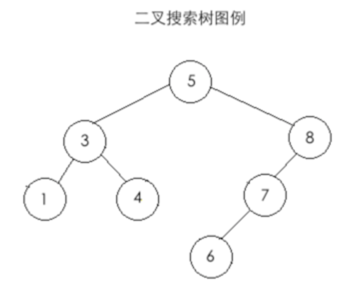
下面具体来实现level_order:
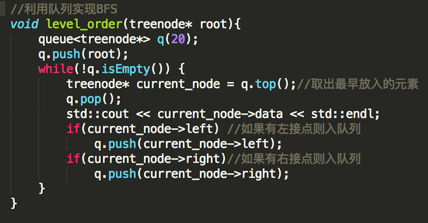
只要理解的队列的先进先出的特点上面的实现比较容易理解,不多解释,编译运行:

下面看一下它的时间复杂度:由于队列中有多少元素就会遍历多次次,所以很明显是O(n)。