这次终于要开始学习跟生活昔昔相关的算法了，首先映入眼帘的是归并排序，对于什么是归并排序网上文章一大堆，这里再来明确一下，先来看一张原理图【下面会用程序来论证整个如图所示的递归合并过程】：
而看一下归并排序的文字描述，理论跟实践相结合：
对思路清楚之后，下面则具体实现一下，实现方法有两种：递归、非递归。具体如下：
递归方式实现归并排序[自顶向下]：
先编写基础框架：
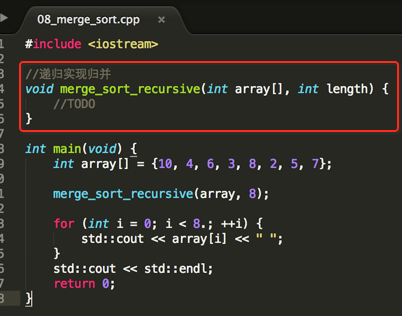
上面先贴出具体实现，然后下面会基于实现一步步去分析其实现原理:
#include <iostream> //合并两个已经排好序的数组 void merge(int array[], int temp[], int left, int middle, int right) { int p_left = left, p_right = middle; int i = left; while(p_left < middle || p_right < right) { if(p_left >= middle) { temp[i] = array[p_right]; p_right++; } else if(p_right >= right) { temp[i] = array[p_left]; p_left++; } else if(array[p_left] > array[p_right]) { temp[i] = array[p_right]; p_right++; } else { temp[i] = array[p_left]; p_left++; } i++; } for (int i = left; i < right; ++i) { array[i] = temp[i]; } } //其中是一个[left, right)闭开区间 void merge_sort_recursive(int array[], int temp[], int left, int right) { if(right - left <= 1) return; int middle = (left + right) / 2; merge_sort_recursive(array, temp, left, middle); merge_sort_recursive(array, temp, middle, right); merge(array, temp, left, middle, right); } //递归实现归并 void merge_sort_recursive(int array[], int length) { int* temp = new int[length]; merge_sort_recursive(array, temp, 0, length); delete []temp; } int main(void) { int array[] = {10, 4, 6, 3, 8, 2, 5, 7}; merge_sort_recursive(array, 8); for (int i = 0; i < 8.; ++i) { std::cout << array[i] << " "; } std::cout << std::endl; return 0; }
编译运行:
是不是对上面的实现一头雾水，没关系，我也一头雾水，下面来剖析它，通过实现再去整理出实现原理，最终再彻底掌握它：
这里将数组{10, 4, 6, 3, 8, 2, 5, 7}通过递归实现归并达到排序的整个过程一步步展现出来，首先看下归并入口方法：
下面就按程序的三步骤来分析，完全按程序实现的逻辑顺序来：
①、int* temp = new int[length];
为啥要用一个跟数据长度一样长的临时变量呢？实际上就是用它进行数据排序的，将排好序的数据到时再同步到真正的数组中去，具体可以在分析流程②上可以看出来。
②、merge_sort_recursive(array, temp, 0, length);【核心】
接着它会调用另一个重载的方法：
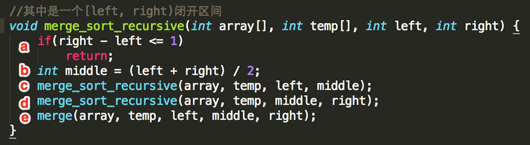
其中传过来的参数left=0,right=8，其中需要特别注意的是是包含left，不包含right，是一个闭开区间。
a、
这是递归结束条件，也就是表示只剩一个元素了，具体可以在分析c、d步骤中去理解,很显然此时为false。
b、取出中间元素的位置，其中归并排序的思想就是以中间为分界，左边排好序，右边再排好序，最后再左右进行合并则达到归并排序的目的。这里取值是：middle=(0+8) / 2 = 4;
c、对[left，middle)这个区间进行递归调用,也就是merge_sort_recursive(array, temp, 0, 4)：
接下来具体来分析一下整个递归过程，还是按着merge_sort_recursive的四部步骤去分析：
ca、
,right=4，left=0，right-left=4，不是小于1的，所以条件不成立，继续往下执行。
cb、
，middle = (0 + 4) / 2 = 2;
cc、
,merge_sort_recursive(array, temp, 0, 2)，可见又进行一个递归过程，继续分析：
cca、,right=2, left=0, right-left=2，不是小于1，所以条件不成立，继续往下执行。
ccb、，middle = (0 + 2) / 2 = 1;
ccc、, merge_sort_recursive(array, temp, 0, 1)，继续递归
ccca、，right=1, left=0, right-left=1,条件刚好成立，于是乎整个方法都返回递归结束。
ccd、
, merge_sort_recursive(array, temp, 1, 2)，继续递归
ccda、，right=2, left=1, right-left=1,条件刚好成立，递归结束。
这时数据调用的关系如下：
cce、
，merge(array, temp, 0, 1, 2),那这个merge方法调用完之后会是什么效果呢？下面具体分析一下流程：
其中参数left=0, middle=1, right=2,下面具体分析：
ccea、
,p_left=0, p_right=1
cceb、
,i=0，这个变量是干嘛用的呢？其实它就是用来将排好序的一一加到temp临时数组，而每添加一个则累加一次，这个在下面步骤中可以很清楚的看到。
ccec、开始不断循环进行比较，其实这个过程跟上节学的排好序的合并链表思想是一模一样的，从代表风格可以看出来，只是这里采用指针位置移位的方法。
loop1: 其中循环条件：(0 < 1 || 1 < 2)，条件为真,则通往循环体：
ccec①、(0 >= 1)，条件不满足，执行条件②；
ccec②、(1 >= 2)，条件不满足，执行条件③；
ccec③、(array[0] > array[1])=(10 > 4)条件满足，则执行条件里面的语句：
temp[0] = array[1] = 4，也就是先取两数中较少的放到temp中
p_right++ ====> p_right=2
ccec⑤、i++ ====> i=1
loop2: 其中循环条件：(0 < 1 || 2 < 2)，条件为真,则通往循环体：
ccec①、(0 >= 1)，条件不满足，执行条件②；
ccec②、(2 >= 2)，条件满足，执行条件里面的语句；
temp[1] = array[0] = 10，也就是将两数中较大的放到了temp中
p_left++ ====> p_left=1
ccec⑤、i++ ====> i=2
loop3: 其中循环条件：(1 < 1 || 2 < 2)，条件为假，退出循环。
cced:将temp中的元素一一复制到目标array数组中，目前temp只有两个已经从小到大排好序的数据：4,10
这时可以看到2左边的元素已经排好序了：
cd、，merge_sort_recursive(array, temp, 2, 4), 由于已经分析了cc的整个递归过程，这里就不仔细分析它了，流程上跟cc是一模一样的，经过这步之后，整个递归的情况如下：
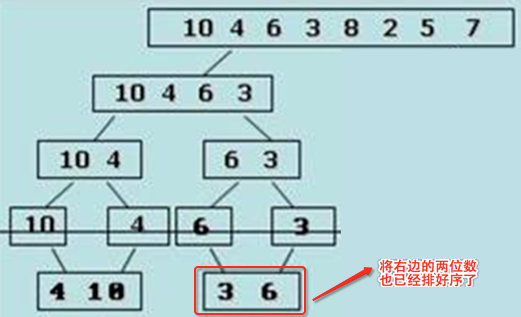
以上cc、cd两步骤就对2左边的数和右边的数进行了从小到大的顺序排序了
ce、，merge(array, temp, 0, 2, 4),经过上面cce的详细分析合并过程，其实就是对[4、10]和[3、6]两个已经排好序的进一并合并成[3、4、6、10]这样从小到大的序列，下面详细按cce的步骤再来熟悉一下整个的合并过程：
其中参数left=0, middle=2, right=4,下面具体分析：
cea、,p_left=0, p_right=2
ceb、,i=0，这个变量干嘛用应该就不用多解释了，上面已经分的过。
cec、开始不断循环进行比较，具体不多解释，主要分析循环的整个过程：
loop1: 其中循环条件：(0 < 2 || 2 < 4)，条件为真,则通往循环体：
cec①、(0 >= 2)，条件不满足，执行条件②；
cec②、(2 >= 4)，条件不满足，执行条件③；
cec③、(array[0] > array[2])=(4 > 3)条件满足，则执行条件里面的语句：
temp[0] = array[2] = 3，也就是先取两数中较少的放到temp中
p_right++ ====> p_right=3
cec⑤、i++ ====> i=1
loop2: 其中循环条件：(0 < 2 || 3 < 4)，条件为真,则通往循环体：
cec①、(0 >= 2)，条件不满足，执行条件②；
cec②、(3 >= 4)，条件不满足，执行条件③；
cec③、(array[0] > array[3])=(4 > 6)条件不满足，执行条件④；
cec④、temp[1] = array[0] = 4;
p_left++ ====> p_left=1;
cec⑤、i++ ====> i=2
loop3: 其中循环条件：(1 < 2 || 3 < 4)，条件为真,则通往循环体：
cec①、(1 >= 2)，条件不满足，执行条件②；
cec②、(3 >= 4)，条件不满足，执行条件③；
cec③、(array[1] > array[3])=(10 > 6)条件满足，则执行条件里面的语句：
temp[2] = array[3] = 6，也就是先取两数中较少的放到temp中
p_right++ ====> p_right=4
cec⑤、i++ ====> i=3
loop4: 其中循环条件：(1 < 2 || 4 < 4)，条件为真,则通往循环体：
cec①、(1 >= 2)，条件不满足，执行条件②；
cec②、(4 >= 4)，条件满足，则执行条件里面的语句：
temp[3] = array[1] = 10;
p_left++ ====> p_left=2;
cec⑤、i++ ====> i=4
loop5: 其中循环条件：(2 < 2 || 4 < 4)，条件为假，退出循环。
ced:将temp中的元素一一复制到目标array数组中，目前tempr的序列就如我们猜想的[3、4、6、10]
这时经过这个合并可以看到已将2左边和右边已排好序的数列合并成从小到大了：
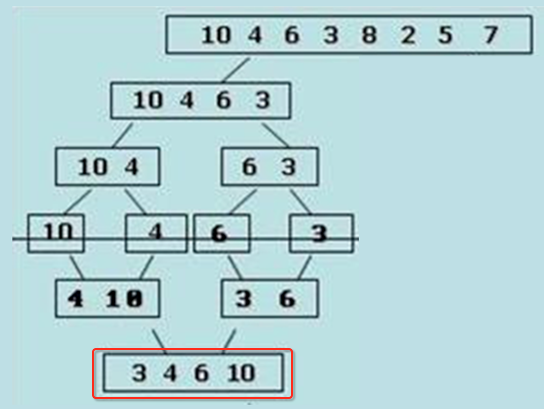
d、依照c的步骤，对[middle，right)这个区间进行递归调用,也就是merge_sort_recursive(array, temp, 4, 8);
这里就不一一分析递归过程了，具体详细递归全并过程已经在c步骤中进行了描述，贴出最终结果：
e、
merge(array, temp, 0, 4, 8)，也就是最终将4左侧已经排好序的[3、4、6、10]和右侧已经排好序的[2、5、7、8]进行最终合并，达到整体从小到大的排序，到这一步也就是整个递归归并实现的全过程，如图：
从上面这符图就可以清楚的知道是一个自顶向下的归并过程。
③、delete []temp;
当临时数组用完之后，需要将其内存释放，不多解释。
这样整个递归实现归并算法的流程走完，有木有茅塞顿开呢？下面再来总结一下实现思路，以便在要忘得差不多的时候自己从头写时有一个思路参考【以C++实现为例】：
步骤1、先声明一个临时数组，数组的长度则跟待排序的数组一样，其主要目的就是为了将排序之后的数组放在它里面，而不是直接去改原数组的序列，等所有步骤结束之后这个数组就是一个已经排好序的数列了，接着再将它原封不动的拷贝到原数组达到最终排序的目的。
步骤2、声明一个方法专门用来递归实现归并，也就是最核心的方法，其参数为：原数组、临时数组、要归并的数组起始位置left【从0开始，是个闭区间】、要归并的数组结束位置right【这是数组的长度，是个开区间】，而该方法具体实现分如下步骤：
a、先来判断递归的结束条件，这是很关键的，而条件就是发现只有一个元素了则结束递归，而如何判断只剩一个元素了呢？用right-left <= 1，其实很好理解，因为是一个[left,right)的闭开区间，当还剩一个无毒时，left=0、right=1。
b、计算出中间的位置，因为归并排序的核心思想就是折半之后将左边和右边的数据排序好，然后再将左右排序好的数据进行合并。
c、不断递归左边的数据，相当于一个数据拆解的过程，直到只剩一个元素结束递归，其参数为：原数组、临时数组、left，middle。
d、不断递归右边的数据，相当于一个数据拆解的过程，直到只剩一个元素结束递归，其参数为：原数组、临时数组、middle，right。
e、将左右两边已经排好序的数据进行合并，这个就跟上篇学习的合并已经排好序的链表逻辑类似，其具体合并的过程如下：
①、声明两个临时变量p_left、p_right，分别指向left、middle，然后会不断的循环去更改这两个临时变量去进行数据合并。
②、声明一个变量i，默认直接指向参数中的left，它的作用主要是用来往temp指定位置塞数据用的，而往temp塞数据是会让一定顺序进行的。
③、接着开始循环进行合并，也是该方法的核心：
1、首先循环的条件是：p_left < middle || p_right < right。也就是左边的数据和右边的数据都走完了则循环结束，条件满足则下执行循环体
2、如果左边的数据已经走完，则将p_right指向的数放到temp中，并且p_right++。
3、如果右边的数据已经走完，则将p_left指向的数放到temp中，并且p_left++。
4、如果左边的数据大于右边的数据，则将右边的数据放到temp中，并且将p_right++。
5、否则表示左边的数据小于右边的数据，则将左边的数据放到temp中，并且将p_left++。
6、最后将i++,将temp的下标往下挪。
f、将temp已经排好序的完全拷贝至array中。
步骤3、将临时变量的内存释放掉，因为它的使用价值已经到此结束。
非递归方式实现归并排序[自底向上]：
非递归的方式整体步骤跟递归的思路是相反的，有了递归的思路，非递归的方式很容易理解，依然看一张用非递归方式来实现归并排序的整体思路：
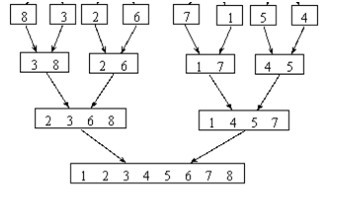
实基本思想是：将数组中的相邻元素两两配对。用Merge()函数将他们排序，构成n/2组长度为2的排序好的子数组 段，然后再将他们合并成长度为4的子数组段，如此继续下去，直至整个数组排好序。下面看下具体实现：
编译运行：
下面依然用debug的方式一步步分析来理解其实现：
①、int* temp = new int[length];不多解释，跟递归实现的一样。
②、接着开始循环开启归并模式，如下：
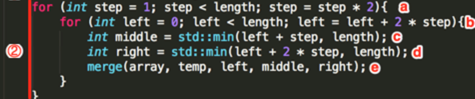
step loop1:
a、
：外层循环，具体为啥这么写等整个过程分析完之后就明白了。
b、
：内层循环,计算left的位置。
left loop1: step = 1、left = 0;
abc、
：计算middle的位置：middle = min(0 + 1, 8) = 1
abd、
：计算right的位置：right = min(0 + 2 * 1, 8) = 2
abe、
：这个方法有木有很熟悉，木错，用的跟递归的合并方法一模一样，所以这里就不多解释了。
left = left + 2 * step = 0 + 2 * 1 = 2;
left loop2: step = 1、left = 2;
abc、：计算middle的位置：middle = min(2 + 1, 8) = 3
abd、：计算right的位置：right = min(2 + 2 * 1, 8) = 4
abe、
left = left + 2 * step = 2 + 2 * 1 = 4;
left loop2: step = 1、left = 4;
abc、：计算middle的位置：middle = min(4 + 1, 8) = 5
abd、：计算right的位置：right = min(4 + 2 * 1, 8) = 6
abe、
left = left + 2 * step = 4 + 2 * 1 = 6;
left loop2: step = 1、left = 6;
abc、：计算middle的位置：middle = min(6 + 1, 8) = 7
abd、：计算right的位置：right = min(6 + 2 * 1, 8) = 8
abe、
left = left + 2 * step = 6 + 2 * 1 = 8;
而内层循环的left < length条件不满足了，则退出此次的内层循环，外层的step = step * 2 = 2
总结：通过上面第一轮内层循环流程走完，外层的step是用来控制是每次比较的数量，而内层的left肯定是用来控制left的位置的，而middle和left就是根据step和left来决定的，其中step每次是+2，而left则是每次基于上一次+2倍的step。
step loop2:
a、：外层循环
b、：内层循环
left loop1: step = 2、left = 0;
abc、：计算middle的位置：middle = min(0 + 2, 8) = 2
abd、：计算right的位置：right = min(0 + 2 * 2, 8) = 4
abe、
left = left + 2 * step = 0 + 2 * 2 = 4;
left loop2: step = 2、left = 4;
abc、：计算middle的位置：middle = min(4 + 2, 8) = 6
abd、：计算right的位置：right = min(4 + 2 * 2, 8) = 8
abe、
left = left + 2 * step = 4 + 2 * 2 = 8;
而此时left < length不满足条件，此次的内层循环结束。外层的step = step * 2 = 4
step loop3:
a、：外层循环
b、：内层循环
left loop1: step = 4、left = 0;
abc、：计算middle的位置：middle = min(0 + 4, 8) = 4
abd、：计算right的位置：right = min(0 + 2 * 4, 8) = 8
abe、
left = left + 2 * step = 0 + 2 * 4 = 8;
而此时left < length不满足条件，此次的内层循环结束。外层的step = step * 2 = 8，而外层的step<length也不满足条件，则外层循环也结束，至此整个非递归方法结束。
③、delete []temp;也不多解释。
以上详细的对归并的两种实现方法分析了其实现过程，算法实现完了当然得分析一下它的时间复杂度，这个待下次学习快速排序之后再一次分析~因为他们的时间复杂度是一样的。