接下来要学习跟排序相关的算法了,在正式之前先来个小热身,将两个“已排好序”的链表进行merge操作,先编写一个代码框架,这个比较简单不过多解释:
#include <iostream> struct node{ int payload; node* next; node(int payload) { this->payload = payload; next = nullptr; } }; class linkedlist { node *head, *tail; public: linkedlist() : head(nullptr), tail(nullptr) { } //从尾部插入元素 void push_back(int value) { //TODO } //输出链表元素 void output() { //TODO } }; linkedlist merge(linkedlist a, linkedlist b) { //TODO return a; } int main(void) { linkedlist a, b; //按顺序插入数据 a.push_back(4); a.push_back(7); a.push_back(20); b.push_back(2); b.push_back(3); b.push_back(9); b.push_back(29); linkedlist result = merge(a, b); result.output(); return 0; }
接着来完善linkedlist类中的方法,对于一个链表通常会有:插入数据、取出数据、弹出数据、判断当前链表是否为空、输出整个链表,下面一一来完善:
#include <iostream> struct node{ int payload; node* next; node(int payload) { this->payload = payload; next = nullptr; } }; class linkedlist { node *head, *tail; public: linkedlist() : head(nullptr), tail(nullptr) { } //从尾部插入元素 void push_back(int value) { if(empty()) { //如果是空链表,则头尾节点都指向新插入的 head = tail = new node(value); } else { tail->next = new node(value); tail = tail->next; } } //获得头一个元素的值 int front() { if(empty()){ throw "The list is empty."; } return head->payload; } //弹出头节点 void pop_front() { if(empty()){ throw "The list is empty."; } node* first_node = head; head = head->next; delete first_node; } bool empty() { return head == nullptr; } //输出链表元素 void output() { node* iterator = head; while(iterator) { std::cout << iterator->payload << " "; iterator = iterator->next; } std::cout << std::endl; } }; linkedlist merge(linkedlist a, linkedlist b) { //TODO return a; } int main(void) { linkedlist a, b; //按顺序插入数据 a.push_back(4); a.push_back(7); a.push_back(20); b.push_back(2); b.push_back(3); b.push_back(9); b.push_back(29); linkedlist result = merge(a, b); result.output(); return 0; }
接下来则是到了如何合并两个链表的关键实现了,如何实现呢?
分以下几个条件来进行思路整理:
1、边界循环条件是两个要合并的链表中不能都为空。
2、如果两个链表中有一个为空链表,那这合并就比较简单了,直接把非空的链表中的元素一个个加到新链表中,然后将非空的链表pop_front()。
3、如果两个链表都没有一个为空的情况,那就是合并算法最核心的啦,其做法也是比较简单的,如下图所示:
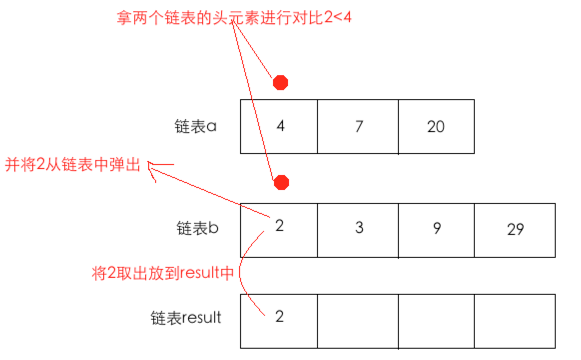
这样结构就变成了:

接着再进行同样的比较,如下:

此时结构就变成了:

以此循环,直到会遇到有个链表为空的情况,如下:

那接下来再次循环,就会走到如下条件了,那就直接将链表b的数据拿到result中既可,如下:
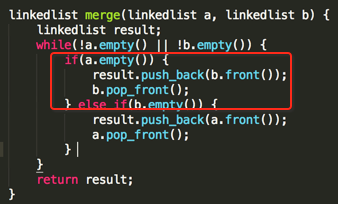
下面将merge方法完善一下:

编译运行:

那这个合并算法的时间复杂度是多少呢?貌似不是特别好算,因为循环条件是一个纯逻辑的东东,看不出具体循环了多少次,这里可以观察一下条件判断,每次条件都会要pop_front(),如下:
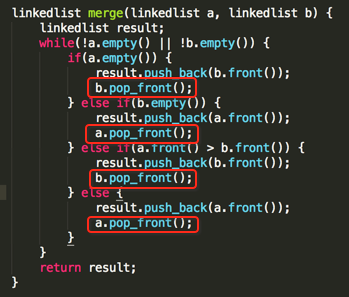
假设链表a的长度是m、链表b的长度是n的话,总共循环应该是(m + n)次,而方法中其它的一些语句都是常量级别的,跟元素个数木有关系:
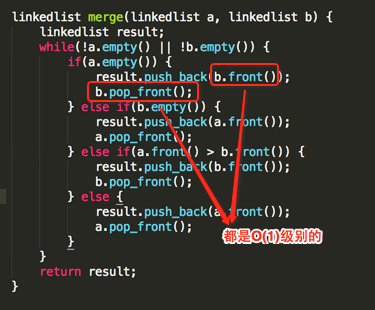
所以整个merge的时间复杂度是:(m + n) * O(1) = O(m + n)