今天是最后一天上班,所以打酱油的时间充分,想着明天就要坐上爱心的突突车返乡了内心真是激动万分呀,既然要过大年了,基本上期间写博客的心思也应该跑得九霄云外了,所以安耐住激动的心必须年前搞一发,也提前预祝各位赏光的大佬们春节快乐~~今年的学习其实落下很多,如kotlin项目、flutter项目、ios、java并发、jvm、算法与数据结构,java全栈,android架构。。。。还想学的有基金理财、python。。。所以新的一年对于落下的这些定会一个个完整的学完,只是时间的快慢,也想看自己在何时会放弃,期待自己放弃的那一天~~其实吧,人生不就是一场马拉松比赛嘛,到达终点的方式很多,其中也会遇到各种各样的问题,而只要保持耐力持之以恒的往前在走,享受其中的过程,慢慢到达预期的终点就行了,重点是按着自己的节奏一步一个脚印走就行了。。。。打住,先拐回来,还是开始这次的线性代数的学习。
在上一次https://www.cnblogs.com/webor2006/p/14271706.html中学习了矩阵变换在图形学中的简单应用,其中对待看待矩阵有一个非常重要的视角就是可以把矩阵看作是对一个系统的描述,更准确地来说是对线性系统的描述,所以这次来学习一下当把矩阵看作是对线性系统的描述之后如何用矩阵来解决线性系统的相关问题。
什么是线性系统:
其实对于线性系统就类似于初中小学所学的线性方程组的概念,比如这么一个二元一次的方程组:

那线性系统中的“线性”又是指啥呢?其实是指未知数只能是一次方项【如此方程式中的x,y都是一次方的】。 那反之,也存在非线性方程,比如:
![]()
其中第一个方程的x是2次方;第二个未知数z是1/2次方【开根其实就是1/2次方】;第三个x不是简单的一次方了,而是三角函数,也不是线性的。另外说它们不是线性的还有一个视角就是用绘制函数图像能够非常清晰的看出来,上述三个非线性的方程对应如下三个函数图像:
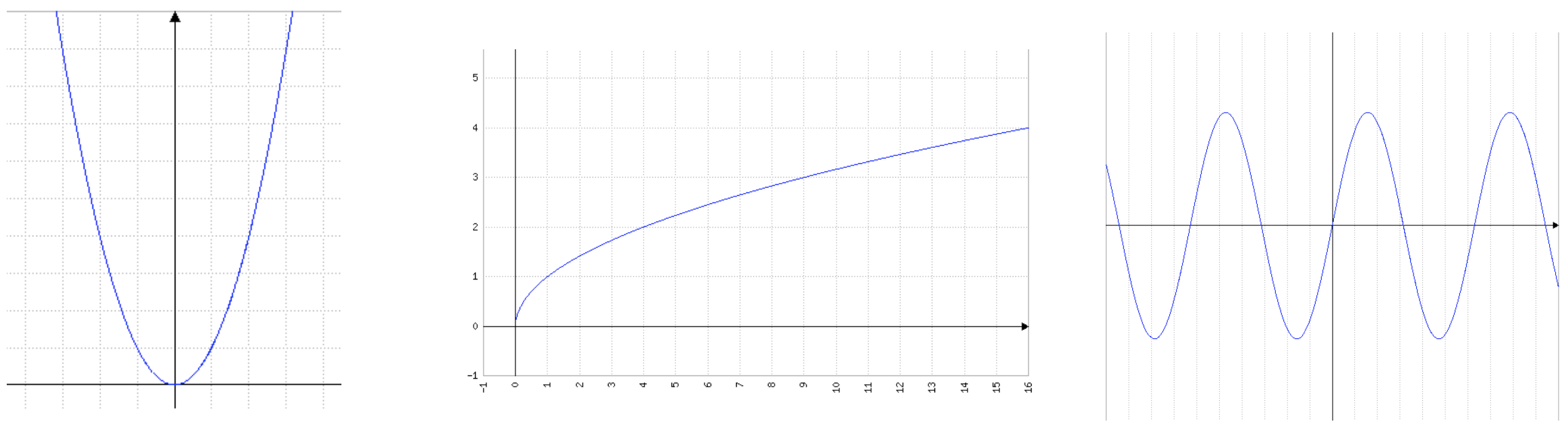
是不是可以看出非线程的图像都是曲线,而非直线,而对于咱们所要研究的“线性”系统其实都是一条直线,比如对于一次方程:
![]()
![]()
它所对应的二维坐标就是直线,如下:

通过这个直观的视角也能加深对于“线性”它所代表的含义,但是!!!对于线性这个词不要就认为它永远表示的是空间中的一条直线,比如对于式子中有三个未知数:

很显然它也是满足线性这个条件的,如果在三维坐标系里其实还表示一个平面,如下:

再回到主题,线性“系统”,上面也说了就是多个线性的方程组织到了一起:
而研究线性系统最为关键的原因就是解决线性系统,换言之就是解上面的方程组。这里要提到的是解方程组看似只是一个计算问题,随着之后的线性代数的深入学习其实对于这样的计算是非常有意义的,不仅仅是能将生活中实际的问题给建模成线性系统的样子【如之前所举例的经济系统、化学系统、电路系统..】,与此同时解线性系统还能解决线性代数这个领域内部抽象的数学问题,不过目前来说只需要看如何来解这个线性系统就成了,而要解上面这个方程组用初中的数学思想就可以使用消元法,啥叫消元法呢?

简言之就是对于一个线性系统中有N个未知数,先想办法消去1个未知数让其变为N-1个未知数,之后再消去一个未知数变为N-2个未知数,依此类推,最后消去只有一个未知数时是不是就能知道该未知数的解了,然后再求出其它未知数,具体咱们来做一次【复习一下初中数学】:

首先来消去x这个数,就让上面那个方程式左边两边都乘以3,然后再拿下面的方程式减去上面的方程式,就会变为:
![]()
此时再将该式子合并同类项,那么经过这次消元之后此方程组就变为:
这样就可以求出y了,如下:
y求出来了,再代入第一个方程式,是不是x也可以求出来了?如下:

为了再巩固一下方程组求解的消元法,再来看一下稍复杂一点的方程组【为啥再巩固一下,因为下面有个概念的思想来自于它】,如下:
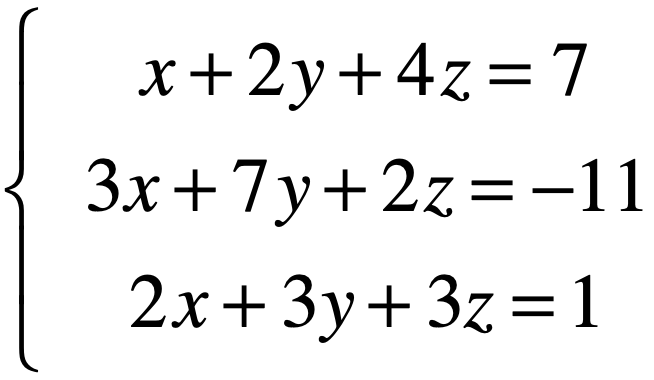
三个未知数,先消掉x,可以让第二个方程减去第一个方程的3倍,所以可以是如下:

接下来再用第三个方程减去第一个方程的2倍,所以可以是如下:
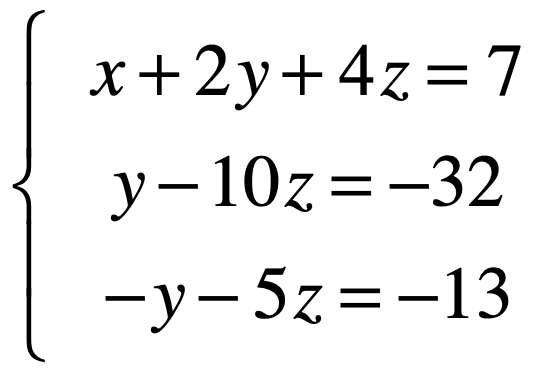
此时对于这两个方程就消去了一个x,只有2个未知数了:

此时就可以把这俩个方程的y消除了,相加既可,如下:

此时未知数z就可以求出来了:

然后再将z代入到第二个方程,所以y也可以求出了,如下:
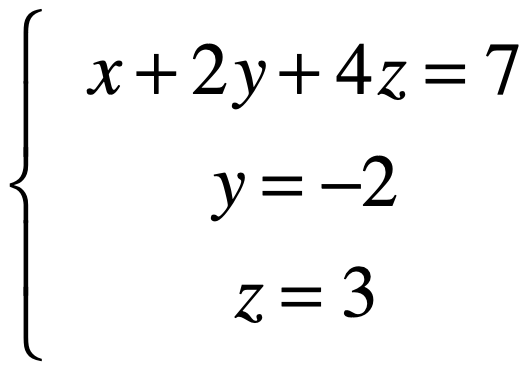
最后再代入第一个方程,其中整个解就出来了:
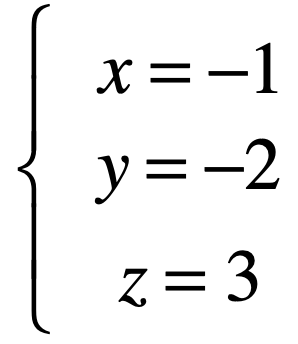
消元法:
对于以上方程组的求解过程就是消元法,最后抽象的总结一下消元法的过程如下:
1、一个方程的左右两边同时乘以一个常数;
2、一个方程加(减)另一个方程;
3、交换两个方程的位置 ;
高斯消元法:
在上一次https://www.cnblogs.com/webor2006/p/14265708.html我们描述了对于一个线性系统也可以很轻松地用矩形进行表达,相应的也可以基于矩阵的操作来解决线性系统相关的问题,背后的思路也很简单,这里还是以这个三元方程来例:
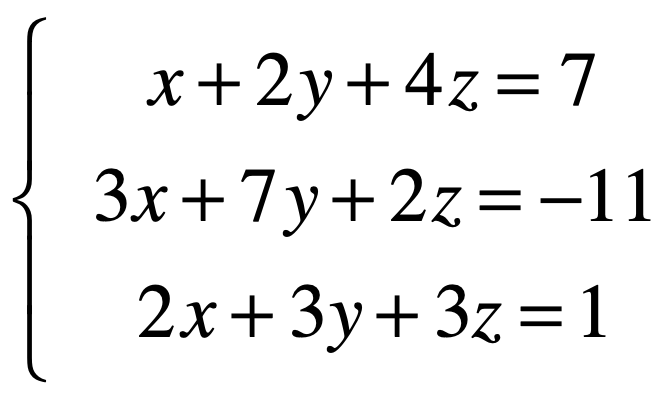
此时方程左边的系数可以用矩阵表示为:

而对于每一个方程的结果又可以表示如下列向量:

而对于未知数表示向量之后整个方程组就可以表示为:
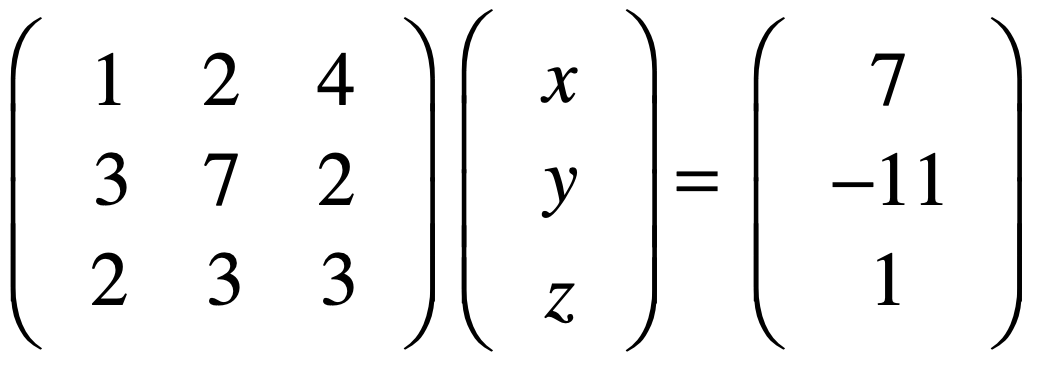
然而在解决线性相关的问题时,可以将未知数给忽略掉,然后将左侧的系数矩阵和右侧的结果向量结合到一起,形成这样:
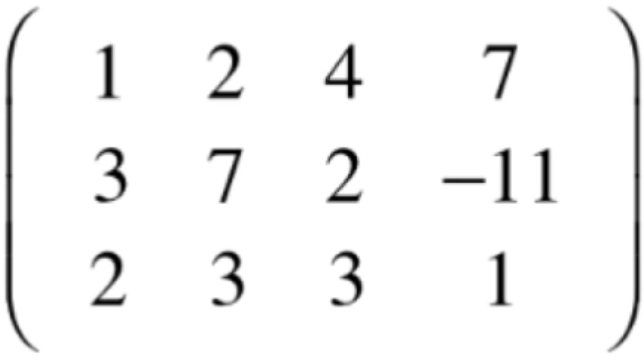
另外再划一条竖线,以区分系数矩阵与结果向量,如下:

而之所有将未知数x,y,z扔掉,是因为它仅仅就是代表有几个未知数而已,你叫a,b,c也可以,u,v,w也可以,而对于未知数的个数其实通过左边系数矩阵的列数就可以反映出来,这也是跟之前学习矩阵x向量的限制条件是相吻合的,因为要求矩阵的列数必须跟向量中的元素是一致的。另外对于系数矩阵的行数其实就代表线性系统中有几个方程,所以基于此,就可以从这个3x3的系数矩阵中看到该系统有3个方程,3个未知数对不?对于上面的这个三行四列的矩阵有一个专用的叫法:增广矩阵,其实也很好理解,也就是在原来的系统矩阵中增加了一列结果,矩阵增加了一些东西所以就是增广了。
既然现在将线性方程组化成了增广矩阵的形式了,那么原来对线性方程组的消元操作也可以直接在矩阵中来完成了,下面以增广矩阵的角度来看一下消元的过程,首先对x消元,其实也就是将第二的方程减去第一个方程的3倍,如下:

然后再来消第三组的x,用第三个方程减去第一个方程的2倍:

此时就可以把这俩个方程的y消除了,相加既可,如下:

此时未知数z就可以求出来了,左右两边都除以-15,第三行就变为:

而接下来照理就应该进行回代的过程,也就是将解出来的z回代到上面的方程进而求解x,y,但是!!!此时先暂停回代,先来总结一下,记得上面对于线性方程组求解过程总结了三点:
1、一个方程的左右两边同时乘以一个常数;
2、一个方程加(减)另一个方程;
3、交换两个方程的位置 ;
而以增广矩阵的视角来看待的话,对应的求解过程的话述相对应的就可以变为:
1、矩阵的某一行乘以一个常数;
2、矩阵的一行加(减)另一行;
3、交换矩阵的两行;
再来对增广矩阵消元的过程进行一个梳理,发现其实就是首先找到第一行的位置将其化成1,然后再把该位置所在列的其它元素化为0,如下:
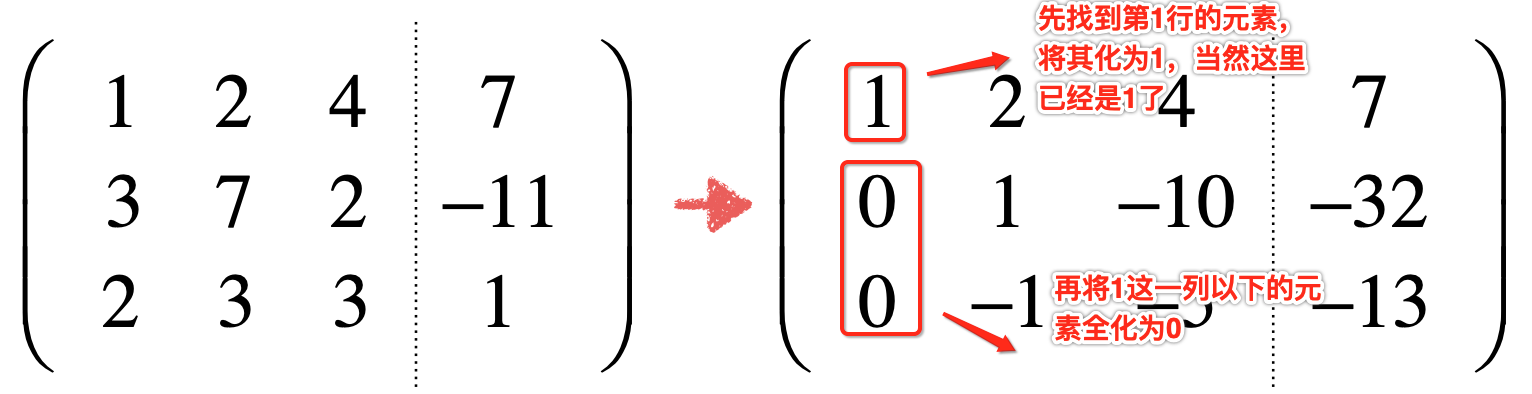
然后再找第二行的第二个元素,将其化为1,再将它所在列下面的其它元素全化为0,如下:
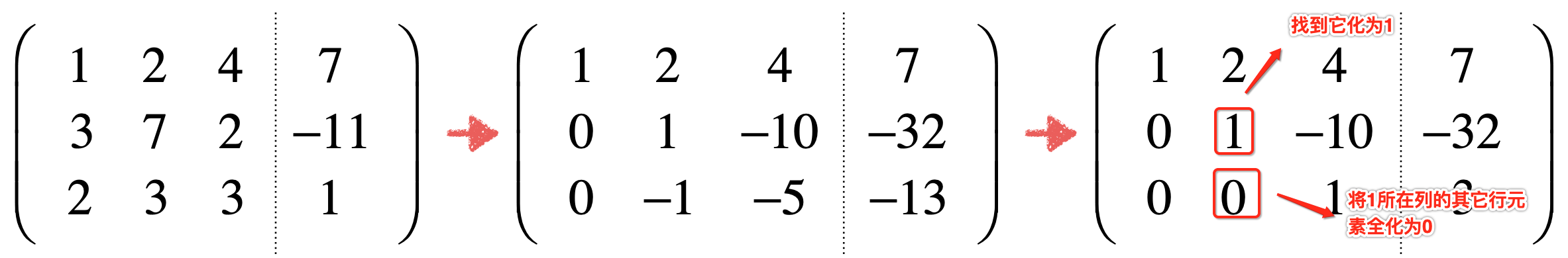
而接下来再拿第三行的第三个元素进行同样的消元,由于第三行下面已经没有元素且本身为1,所以整个消元结束,其中又有一个新名词要出现了:主元(pivot),其实也就是它:

而这样一个消元的过程又有一个名词来表示:高斯消元法(Gauss Elimination),而为了再巩固整个高斯消元的过程,再看几个例子,比如说:

而它对应的增广矩阵为:

接下来开始高斯消元:
- 先找到第一行的主元,也就是在第一行的第一个位置,也就是2,首先将它化为1,所以第一行的元素全部乘以1/2,如下:

此时的主元那就是它了:
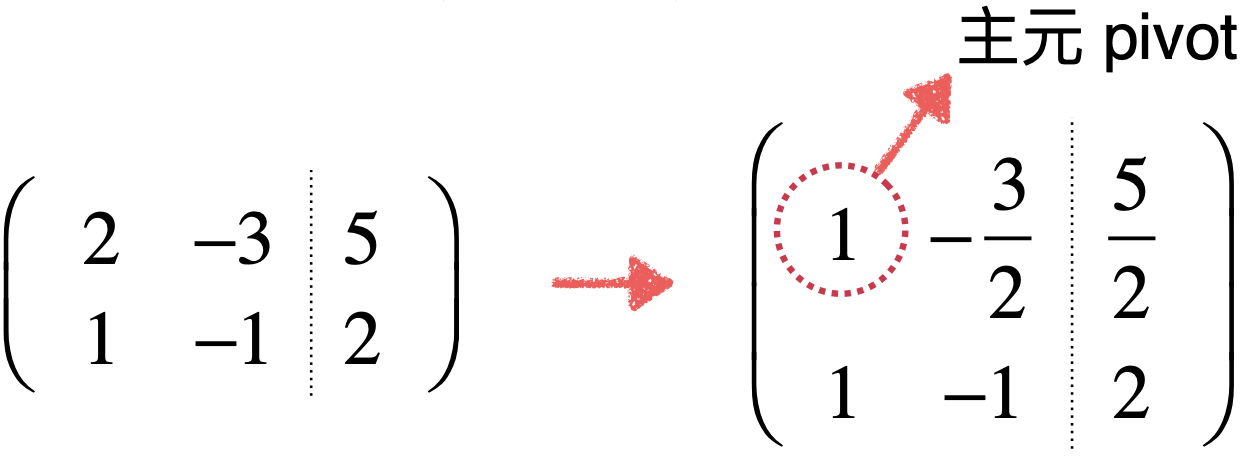
- 将剩下行主元的位置全化为0,也就是主元下面的元素,所以用第二行减去第一行既可,如下:

- 接下来再找第2行的主元,目前是1/2,需要先将它化为1,所以需要乘一下2,所以此时就变为:

此时高斯消元法就已经完成了。
接下来再来另一个例子,这里会涉及到行的交换:

它所对应的增广矩阵为:

开始高斯消元,先找第一行的主元,很显然是0,但是!!要注意了,主元是不允许为0的,因为规则是要让主元化为1嘛,0乘任何数都为0,而且要想将主元位置行的其它元素化为0是永远达不到了,此时怎么办呢?其实可以对行数进行交换,这里既可以让第一行和第二行交换,也可以让第一行跟第三行交换,那具体选择哪行来交换呢?由于之后这块要进行计算机的实现,而在计算机的实现当中通常选数值最大的那一行进行交换,也就是:

而之所以选择这最大的行其实是尽量避免误差,那为啥选大的误差就能尽量避免这块其实是数值分析领域所研究的内容,这里就记住选大的行交换就好了。接下来再进行正常的高斯消元既可,这里就略过了。
但是!!!高斯消元法有一个问题,我们只能通过矩阵读出最后一个未知数的结果,之后还得回代再来得出所有其它未知数的结果,那。。有木有一种方法再继续对矩阵进行变形从而直观的通过矩阵就能知道每一个未知数的解是多少呢?答案是肯定的,往下看。
高斯-约旦消元法:
这里还是先来对咱们的高斯消元法进行一个流程梳理,对于这样一个方程:

高斯消元的过程如下:
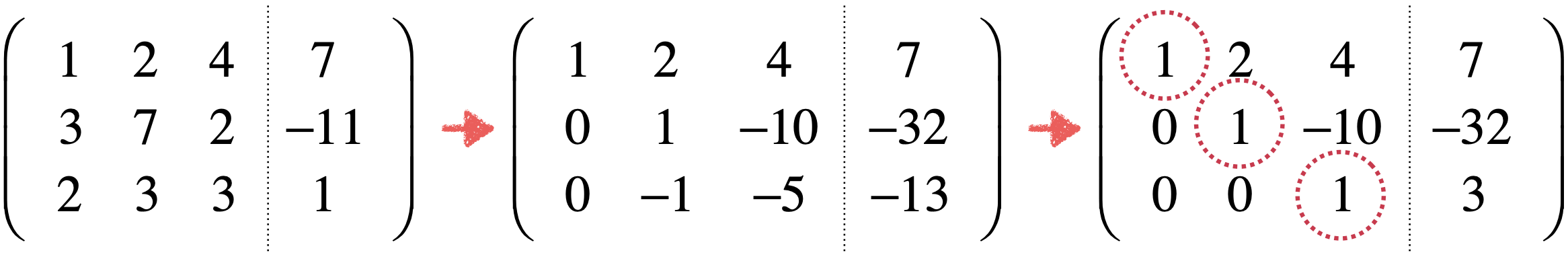
而在上面也说了高斯消元的一个问题就是只能看出z这个未知数的解,对于x,y还看不出,因为此时的方程式其实化成了它:

那还得继续做矩阵变换才行,此时其实将它化为0,对于y的解就出来了:

而将其化为0也很简单,将第三行乘10再跟第二行相加,就变化:

是不是此时就能清晰的通过矩阵的样子看出y的解就为-2了,同样的继续,再将第三个主元列的第一行的4也化成0,其实就是反过来从第三行往第一行再进行一次高斯消元的过程,所以只需要让第一行减去第三行的4倍既可,如下:

此时y的值就为-2了,其对应的线性方程就化简成了:

此时倒数第一行的主元之上元素都已经化为0了,接下来则回到倒数第二行,将它上面的元素化为0了,所以同样的套路,用第一行减去第二行的2倍,变化如下:
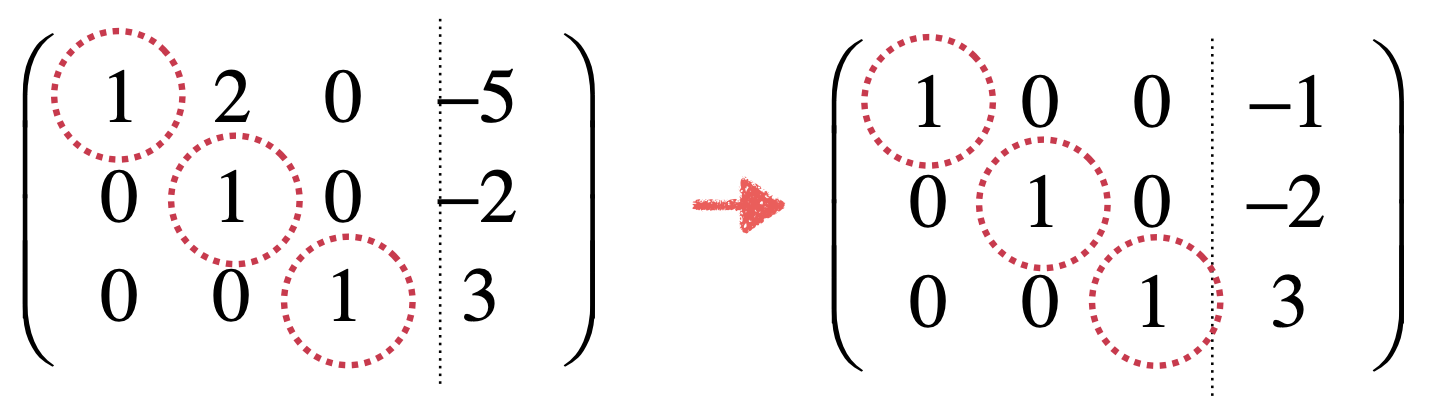
经过这样反着的高斯消元之后,通过矩阵就可以直观看出来所有未知数的解了,如下:

此时对于上面的整个过程又有一个专业名词出现了:高斯-约旦消元法 Gauss-Jordan Elimination,总结一下它的过程分为两个:前向过程(从上到下)和后向过程(从下到上),而具体的步骤如下:
前向过程(从上到下):
1、选择最上的主元,将其化为1;
2、主元下面的所有行减去主元所在行的某个倍数,使得主元下面所有元素都为0;
后向过程(从下到上):
1、选择最下的主元;
2、主元上面的所有行减去主元所在行的某个倍数,使得主元上面所有元素都为0;
不过目前咱们的这种高斯约旦消元的系数矩阵都是针对方阵而言的,那对于非方阵的系数矩阵这里暂时不考虑,待之后再来学习。
实现高斯-约旦消元法:
回到python的世界,来实现一下我们的高斯-约旦消元法。
新建类:

构造函数:
对于构造函数很显然需要一个系统矩阵和一个结果向量,所以定义如下:

首先需要判断一下矩阵的行数需要等于向量的列数,所以先断言一下:

而由于后续的计算中需要不断的使用矩阵的行数与列数,所以先赋值给变量,方便使用:

由于目标咱们只考虑方阵的矩阵,对于非方阵的形式还木有学习到,所以这里也断言一下,待之后扩展之后再来将此断言去掉:

接下来则将系数矩阵A和结果向量b变幻成一个增广矩阵,具体如下:

接下来获取了系统矩阵的i行向量之后,应该还需要往它后面追加一个结果向量的第i个元素在后面对吧?而由于Vector类设计的初衷是一个不可变的,那如何向它后面追加元素呢,其实可以在它里面增加一个append方法,不过这里简单一点,再封装一个获取底层列表的方法,如下:

但是!!!此时是有问题的,因为它返回的引用,在外部的修改都会影响到Vector底层的_values这个集合,所以这里需要返回它的一个拷贝,其实思想跟java类似,那在python中是如何返回数据的拷贝对象呢?如下:

此时就可以调用向量的这个函数然后向它进行元素的追加了,如下:
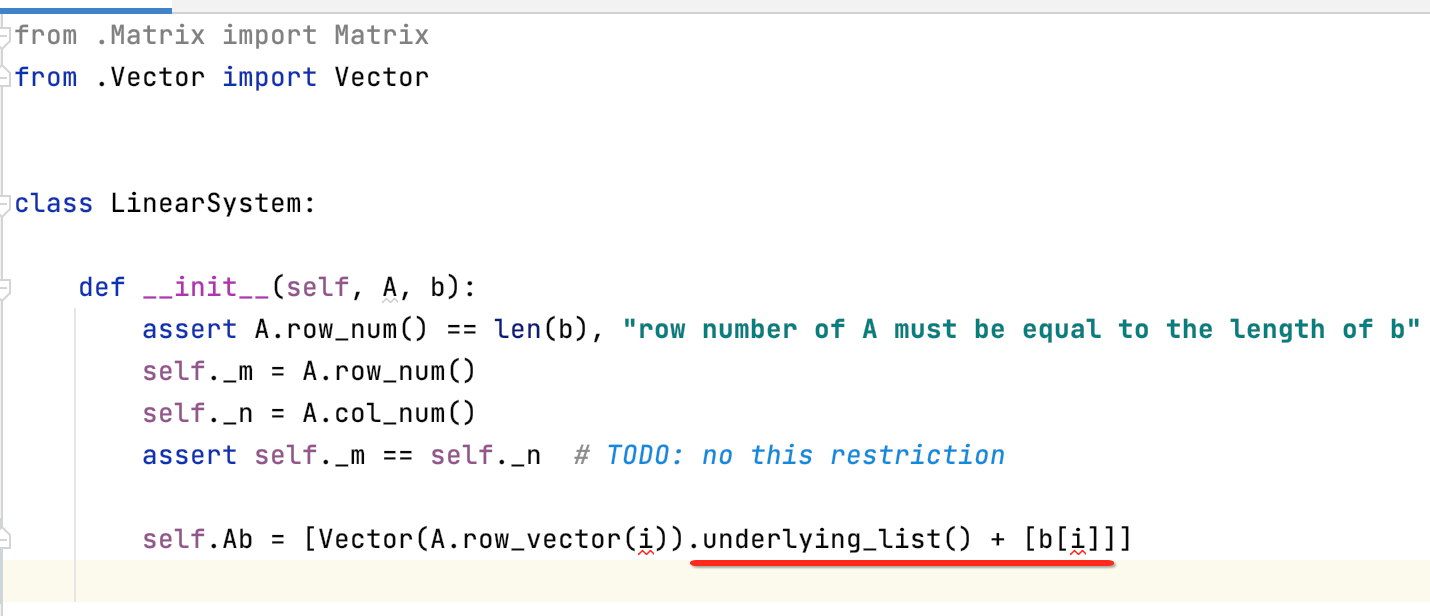
接下来则遍历i既可,如下:

gauss_jordan_elimination():
接下来关键就是来实现高斯约旦消元法了,总的来说它就是两个过程,先来定义一下:

_forward():
对于前项的过程就是循环遍历每行,然后每行遍历时分别对每行的主元化为1,然后再将它所在列的其它行化为0,所以具体实现如下:

这里在找主元时需要考虑一个特殊的情况,就是有可能当前的A[i][i]刚好就是等于0,而根据上面理论的描述,此时需要找它下面最大的元素所在的行进行一下交换,而对于程序的实现就不判断了,直接每次找主元时都遍历找一下,这样结果肯定是木问题的,所以此时先来找i行和n行之间最大的元素,如下:
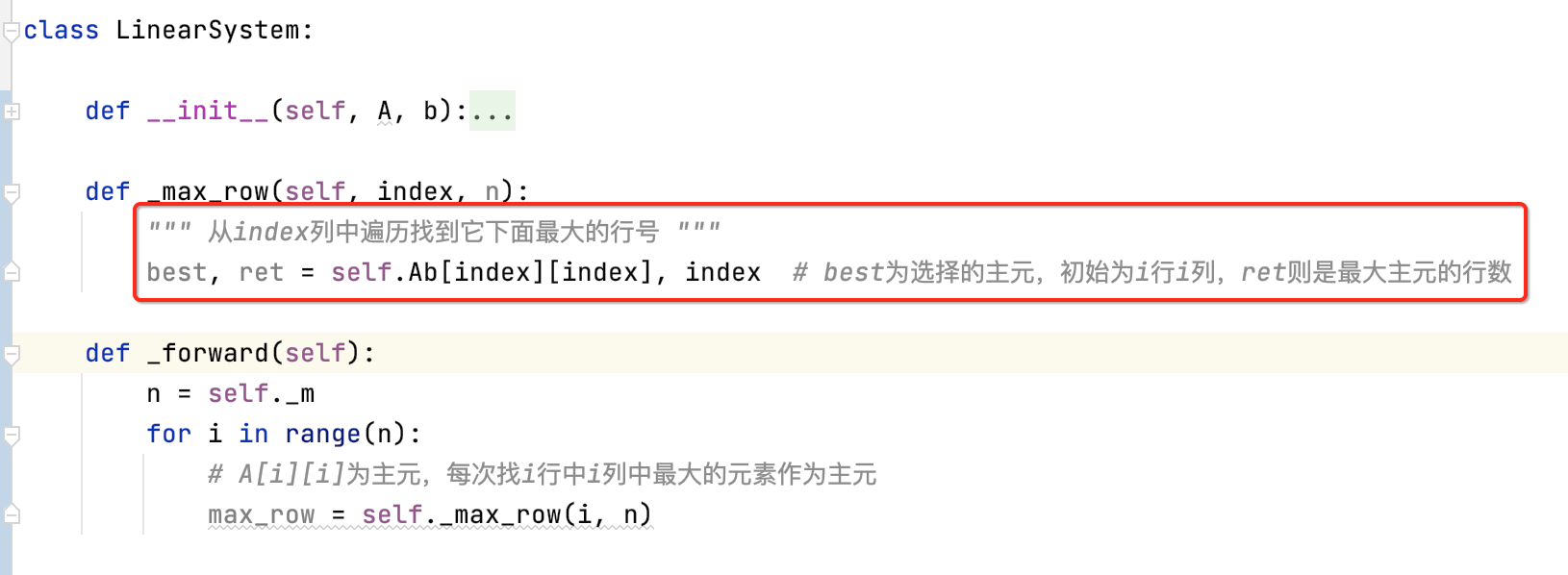
接下来则就往下开始遍历了,逻辑比较好理解,直接贴出来了:

接下来则可以进行两行数据的交换了,而在python中对于矩阵两行数据的交换相当简单,如下:

找到了主元之后,接下来则需要将它归为一,所以如下:

接下来则需要将主元下面的行的元素都化为0,如下:
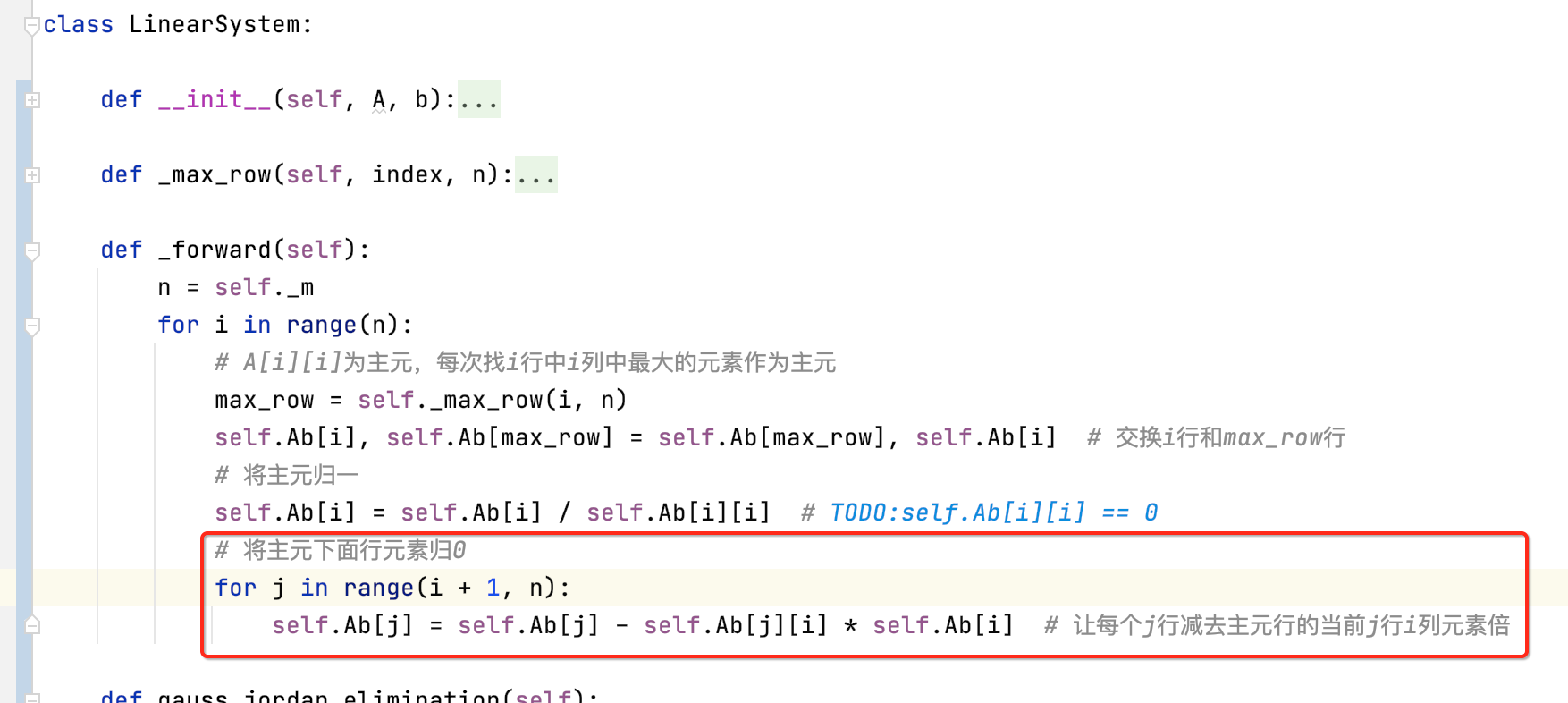
其实也就是实现了高斯消元了,但是还不是高斯约旦消元,因为还差一个后向的过程。
_backward():
有了前向的实现,对于后向的就简单多了,实现如下:

有了它,则是完整的一个高斯约旦消元的过程了。
fancy_print():
接下来打印一下增广矩阵,以便看一下经过高斯约旦之后的增广矩阵的样子,也就是想打印成这种形式:

如下:

然后对于每一行的矩阵元素后面再加一个竖线和对应的结果元素,所以每行结尾不能以回车符,所以这里需要加句话:

然后再来打印结果元素:

测试:
接下来编写测试代码来验证一下:

运行,发现报错了。。

这是因为增广矩阵的初始化有问题,如下:
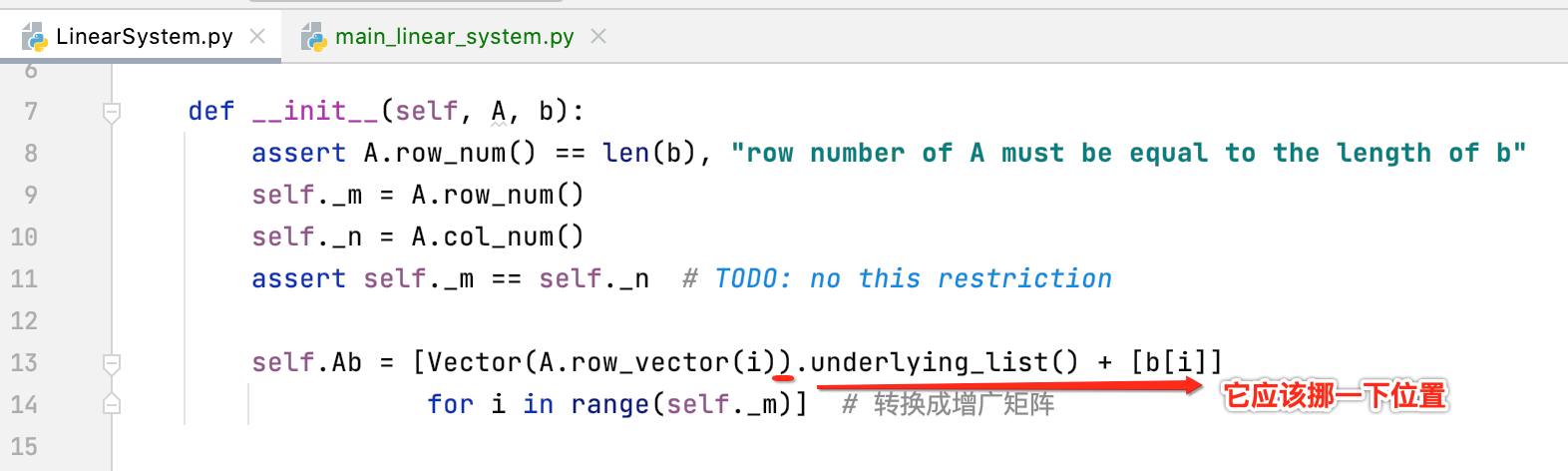

再运行,还是报错。。

那。。这是啥原因呢?debug一下:

为啥返回一个None呢?超级坑,再来往里debug,答案就出来了:
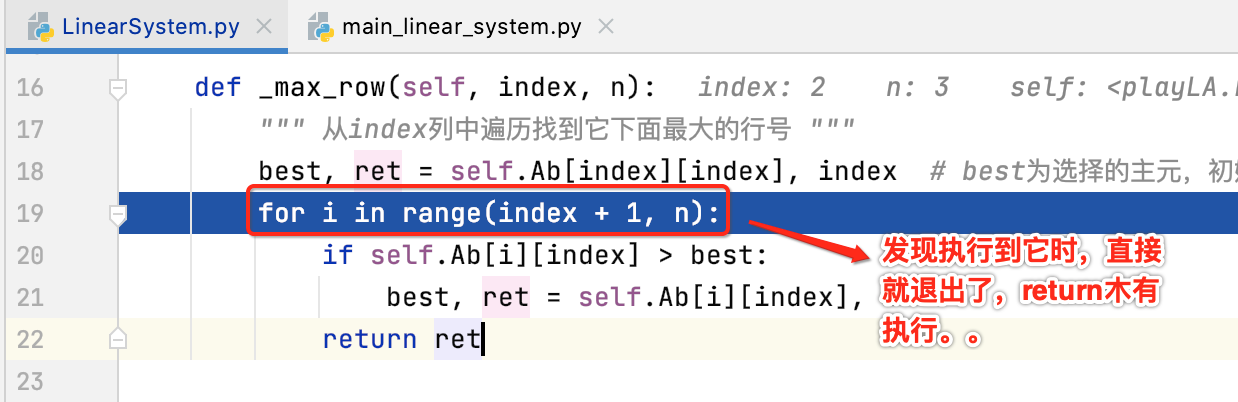
熟悉python的肯定就看到问题了,而对于小白的我,完全没找出来,将它改为它就好了:

所以对于习惯java的人来说,在写python这块一定要注意了,这块确实是比较容易出错,再运行就o了:

这个跟之前理论描述的结果相吻合:

为了更加精准的测试咱们写的程序是无bug的,所以这里再多弄几组测试用例,可以笔算一下,这里就直接贴出来了:
from playLA.LinearSystem import LinearSystem from playLA.Vector import Vector from playLA.Matrix import Matrix if __name__ == "__main__": A = Matrix([[1, 2, 4], [3, 7, 2], [2, 3, 3]]) b = Vector([7, -11, 1]) ls = LinearSystem(A, b) ls.gauss_jordan_elimination() ls.fancy_print() print() A2 = Matrix([[1, -3, 5], [2, -1, -3], [3, 1, 4]]) b2 = Vector([-9, 19, -13]) ls2 = LinearSystem(A2, b2) ls2.gauss_jordan_elimination() ls2.fancy_print() print() A3 = Matrix([[1, 2, -2], [2, -3, 1], [3, -1, 3]]) b3 = Vector([6, -10, -16]) ls3 = LinearSystem(A3, b3) ls3.gauss_jordan_elimination() ls3.fancy_print() print() A4 = Matrix([[3, 1, -2], [5, -3, 10], [7, 4, 16]]) b4 = Vector([4, 32, 13]) ls4 = LinearSystem(A4, b4) ls4.gauss_jordan_elimination() ls4.fancy_print() print() A5 = Matrix([[6, -3, 2], [5, 1, 12], [8, 5, 1]]) b5 = Vector([31, 36, 11]) ls5 = LinearSystem(A5, b5) ls5.gauss_jordan_elimination() ls5.fancy_print() print() A6 = Matrix([[1, 1, 1], [1, -1, -1], [2, 1, 5]]) b6 = Vector([3, -1, 8]) ls6 = LinearSystem(A6, b6) ls6.gauss_jordan_elimination() ls6.fancy_print() print()
运行结果:
/Users/xiongwei/opt/anaconda3/bin/python3.8 /Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/LinearAlgebra/main_linear_system.py 1.0 0.0 0.0 | -1.0 -0.0 1.0 0.0 | -2.0 -0.0 -0.0 1.0 | 3.0 1.0 0.0 0.0 | 1.9999999999999996 -0.0 1.0 0.0 | -3.0000000000000018 0.0 0.0 1.0 | -3.9999999999999996 1.0 0.0 0.0 | -1.9999999999999998 0.0 1.0 0.0 | 1.0 -0.0 -0.0 1.0 | -3.0 1.0 0.0 0.0 | 2.9999999999999996 -0.0 1.0 0.0 | -3.9999999999999996 0.0 0.0 1.0 | 0.4999999999999999 1.0 0.0 0.0 | 3.0 -0.0 1.0 0.0 | -3.0 -0.0 -0.0 1.0 | 2.0 1.0 0.0 0.0 | 1.0 0.0 1.0 0.0 | 1.0 -0.0 -0.0 1.0 | 1.0 Process finished with exit code 0
其中由于浮点运算会有精度问题,所以可能结果看到的跟预期有些偏差,但是其实是近似预期的。不过目前咱们的程序还有很多情况木有考虑,比如非方阵,有些方式组只有一个解,也有些是无解的等等,下面就来解决这样的情况。
线性方程组解的结构:
在上面也抛出了对于咱们目前的实现的问题,接下来则来具体分析一下会出现其它情况的方程组。
方程组无解:
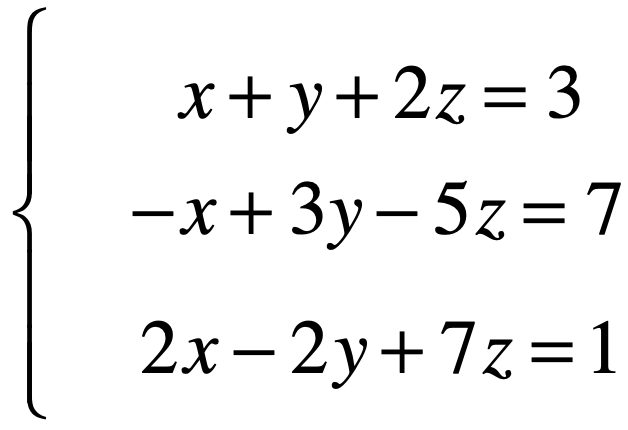
它对应的增广矩阵为:

然后对第一行的主元进行消元就变为:

然后再对第二行的主元进行消元,由于此时主元是4,照理应该要进行归一操作,不过这里简化一下,直接让第二行+第二行将第二行主元下面的归0,如下:

此时,发现矛盾点了:
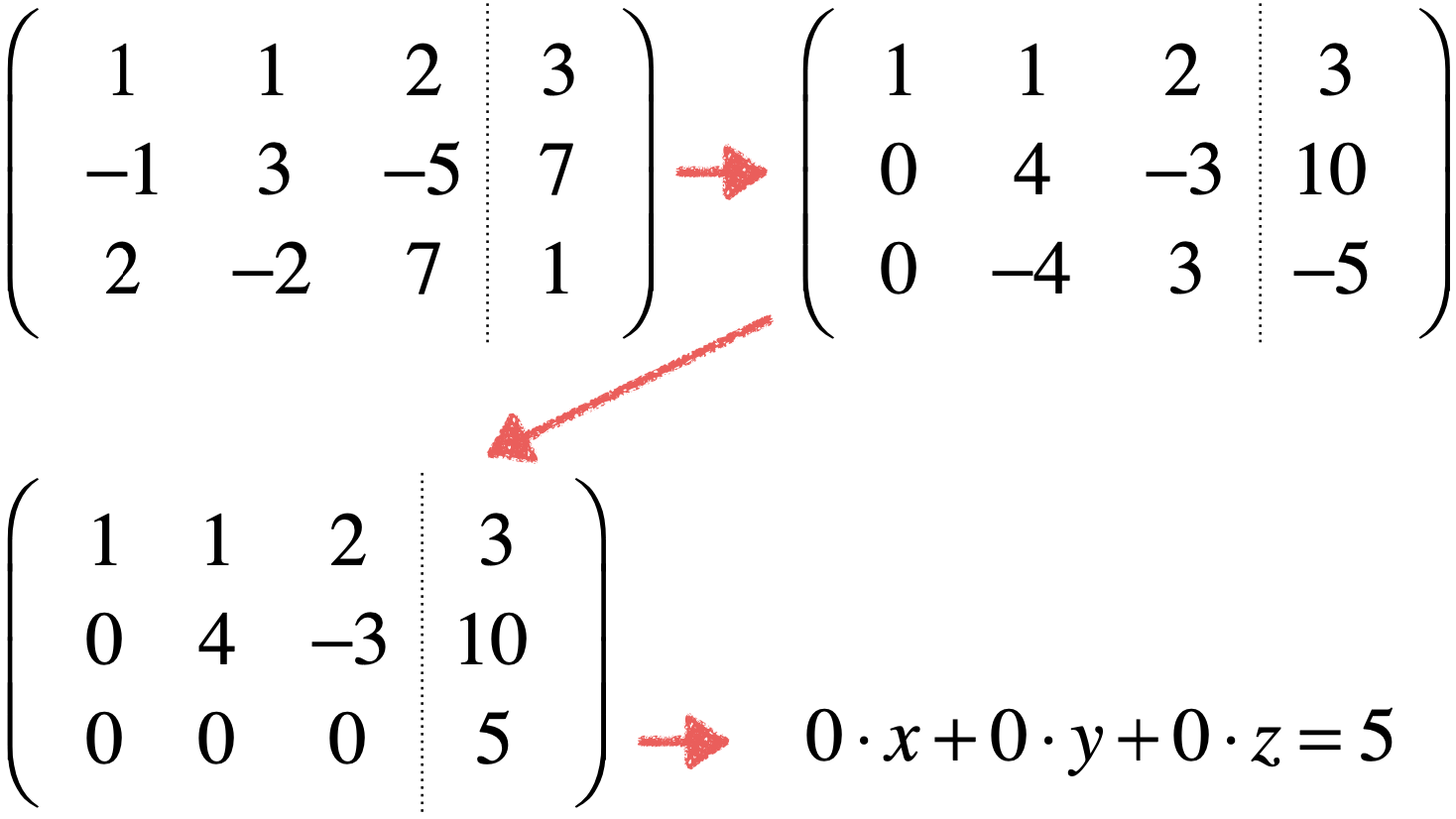
无论如何这个式子也不可能成立对吧?这也就意味着无法找到一个x,y,z满足这个式子了,也就是无解!!!
方程组有无数解:
接下来再来看一个方程组:
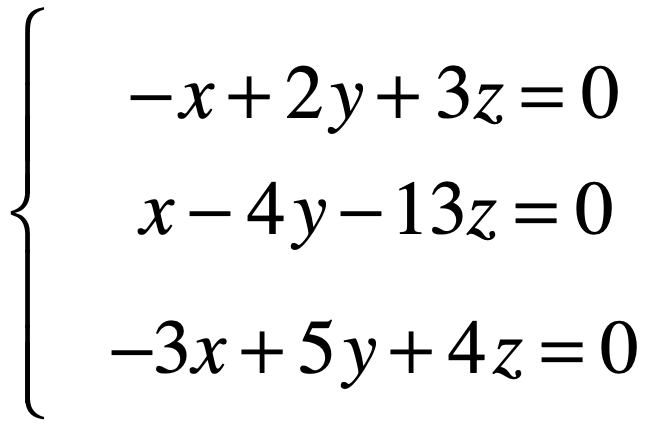
化为增广矩阵:
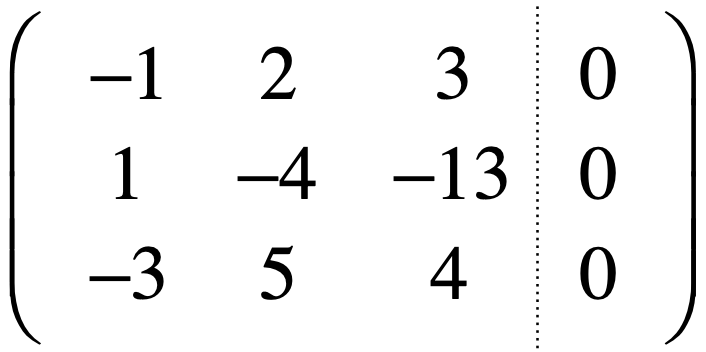
然后处理第一行的主元,将其下面的化为0,变为:

接下来处理第二行的处元,先将它归一:
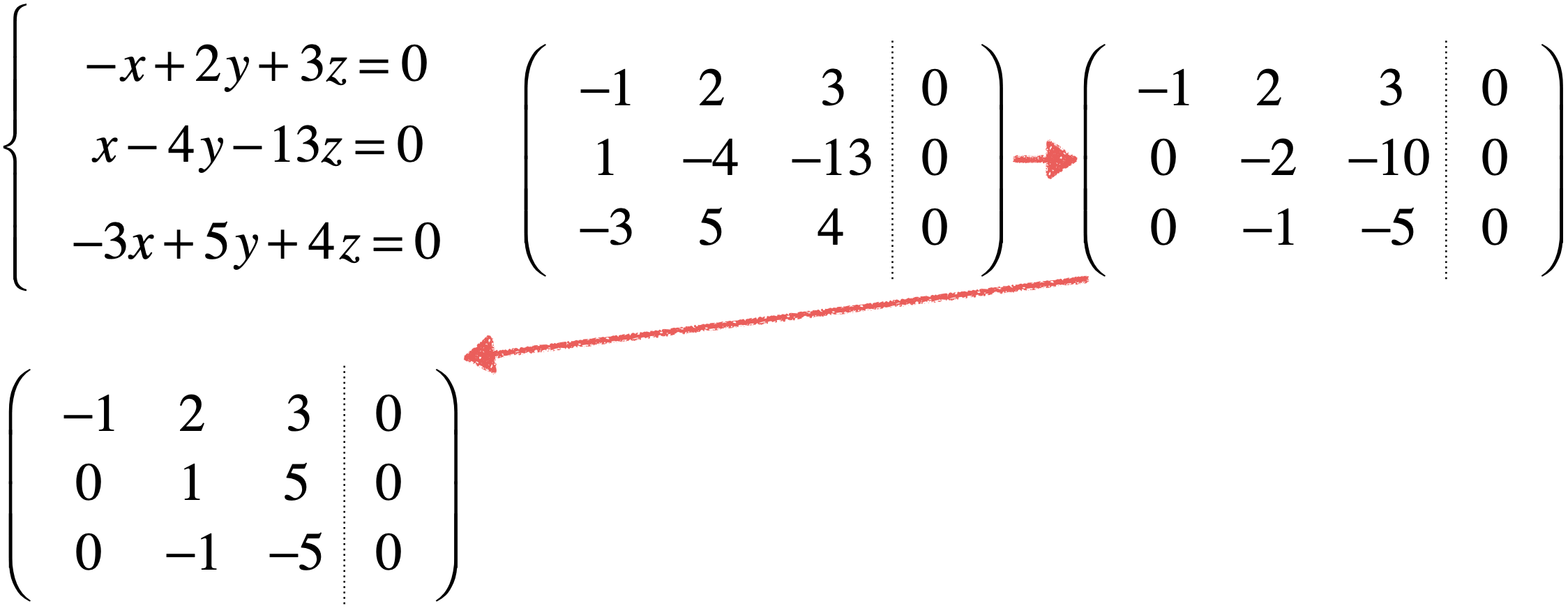
接下来则以第二个主元将其下面的元素归为0,直接第二行+第三行既可:
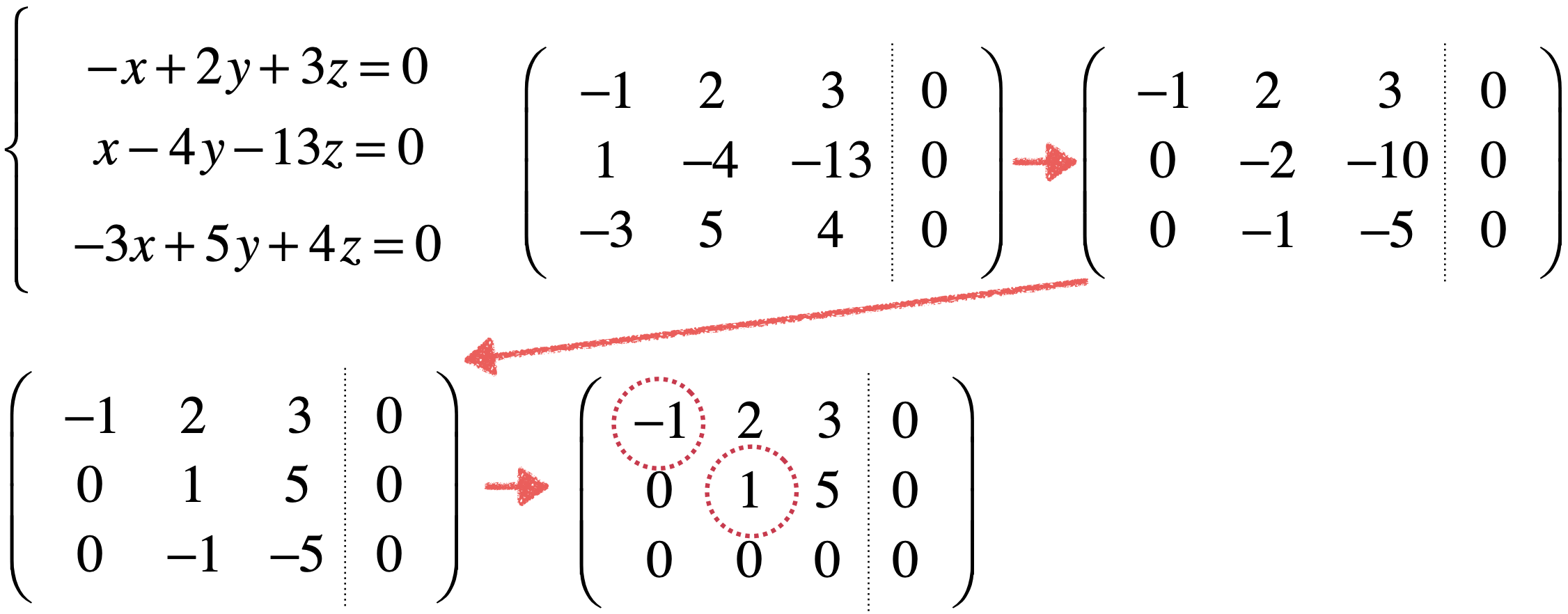
目前高斯消元过程已经结束了,发现此时的最后一行出现了全0行,很显然也是一个有效的等式,因为0*x+0*y+0*z = 0永远恒等,接下来则可以继续往下进行消元,由于最后一行没有主元了,所以回到倒数第二行,将这个主元上面的元素变为0,也就是用第一行减去2倍的第二行,变化如下:

而此时方程式就变为了:

此时再变换一下:

是不是z可以取任意值,都能得到一组x,y,z满足方程组,方程组有无数组解!
三种方程式总结:
接下来总结一下对于方程组的三种解的情况:

对于上面三种情况其实用肉眼已经能分清楚了,但是!!!用一个更严谨的方式来看增广矩阵来得到方程组解的结构是有唯一解,无解、还是有无数解之前,需要在往下学习一个概念。
行最简形式:
其实对于线性方程组的增广矩阵进行高斯消元的过程其实是将增广矩阵变幻成了阶梯型矩阵,如果严格的来说啥是阶梯型矩阵要叙述的条件还是挺麻烦的,但是呢,可以用一种辅助方式来助于理解,比如对于这个有唯一解的增广矩阵,可以这么做个辅助线:

从这个辅助线来看就成了一个阶梯型对不?再仔细观察,其实这个阶梯型的线将矩阵分为两部分,阶梯的下面所有的元素都为0:

所以对于其它两种解的增广矩阵也可以做辅助线如下:

而对于这些矩阵都满足:非零行的第一个元素(主元)为1、主元所在列在其它元素均为0,不过这里又有一个新名词要出现了,也就是经过了高斯约旦消元之后所化成的矩阵叫做行最简形式【reduced row echelon form (RREF)】。为了进一步对这个行最简形式有更深刻的认识,下面再来看其它的一些增广矩阵,因为目前所示的增广矩阵都太标准的【都是三个未知数三个方程】,比如看这么一个:

然后画阶梯辅助线:

其中对于第一行的主元没有在第一个位置也没关系,依然是满足行最简形式。下面再来看一下:

画阶梯辅助线:

也是满足行最简形式,因为首元值都是1,然后它所在列的的其它元素全为0,下面再来看几个不满足行最简形式的增广矩阵:
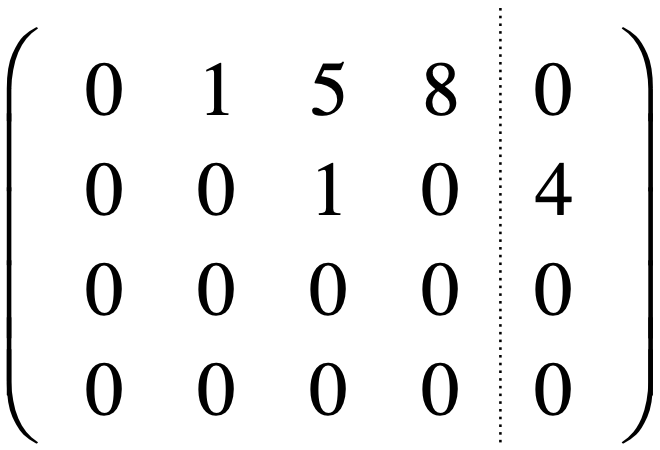
其中主元列中有不为0的:

接下来再来看一个:
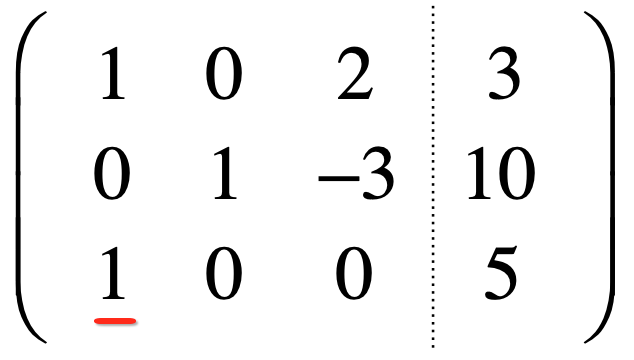
其中标红的主元不满足行最简形式,因为随着行号的上升第三行的主元位置比第二行的主元位置还靠左了,最后再来看一个:

这个为啥不满足行最简形式呢?因为第一行是全0行,对于阶梯型矩阵而言全0行必须是在最后一行。
知道了行最简形式这个概念之后,对于方程有解无解就可以进一步严谨化了,也就是当通过高斯约旦消元之后将增广矩阵化为行最简单形式之后,其实三种形式可以进一步抽象为:

进一步再形象一点可以总结为:
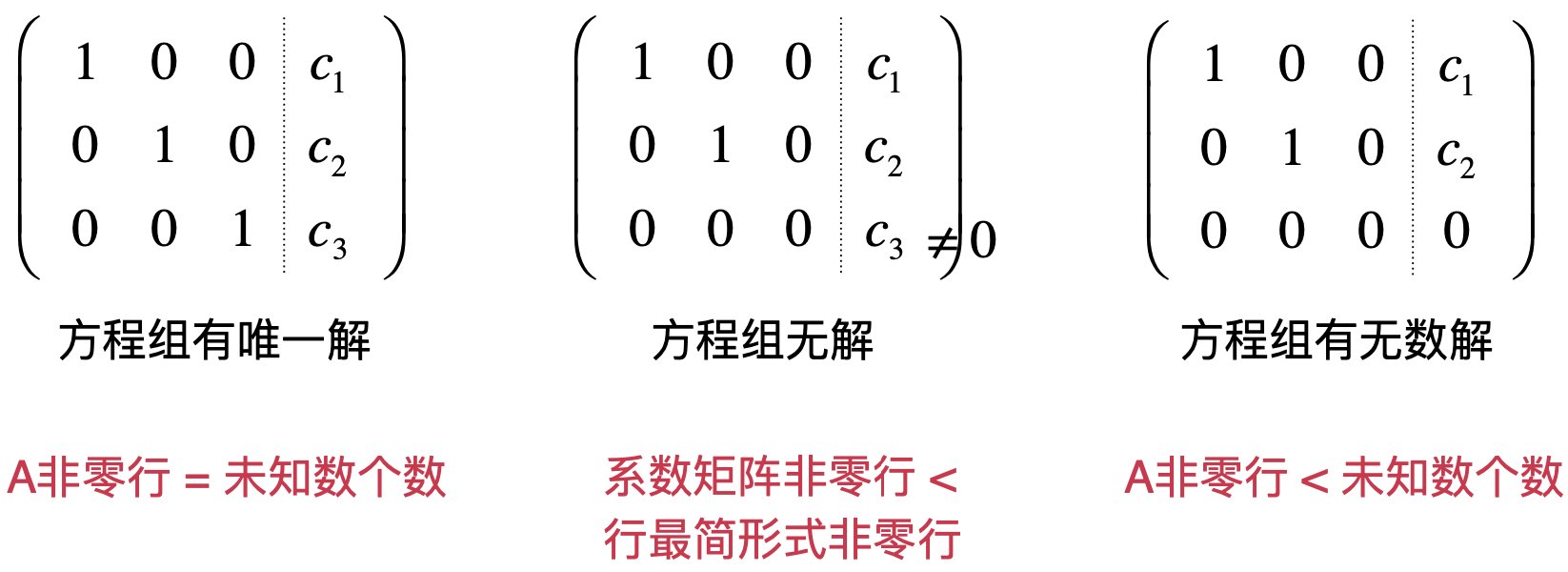
这里要特别注意:一定是要看非零行的个数和未知数的个数,而不能看非零行的个数和整个增广矩阵行的个数,为什么?下面举两个反面例子就知道了,比如说:

它的非零行有3行,而正好跟增广矩阵的3行是一样的,那是不是就应该有唯一解呢?其实它是无解的,因为非零行<未知数个数【目前有四列,也就是有四个未知数】,满足它:

同样的,再来看一个例子:

化为最简形式之后,发现非零行的个数为3,而整个增广矩阵的行数是4,也就是非零行<增广矩阵的行数,是不是无解呢?其实是有无数个解的,这是因为正确的视角得这样看:非零行=未知数的个数【系数矩阵有3列,也就存在3个未知数】,满足它:

而上面这俩反面例子其实已经打破了nxn的系数矩阵了,而是nxm的系数矩阵,也就是方程个数和未知数的个数是不一样的,但是!!依然可以将它化成最简形式来看整个方程式解的结构【有唯一解、无解、无数解】。
直观理解线性方程组解的结构:
目前我们已经知道对于一个方程组的解的类型是通过将方程组化为最简形式之后,判断系统矩阵的非零行和未知数的个数进行一个比较,如果相等则有唯一解,而如果小于则是无数解,否则无解。其实比较的就是方程的数量和未知数的数量的关系,那为什么它们之间的数量不匹配会使得方程组的解的结构产生变化呢?下面以一个直观的视角来进一步理解线性方程组解的结构。
在初高中学习方程组的时候,一定都听过这样的一个概念:“如果一个方程组有n个未知数的话,一定得要有n个方程才有可能有唯一解”,这其实也很好理解,因为每一个方程就代表一个约束条件,如果有n个未知数的话需要有n个约束条件才能把这n个未知数给固定住,
二个未知数:
比如有这么一个方程:
![]()
在二维坐标系中表示的话其实就是一条直线,如下:

而满足这个式子的点n多,不足以求出一个唯一解,但是!!!如果再加一个方程使之成为一个方程组:

此时在二维坐标系中就可以看到有一个相交点了:

此时这个方程就有一个唯一解了,但是!!!在上面的描述中有个词高亮了,就是“可能”,也就是说并非有n个方程n个未知数就一定有唯一解,看下面这个方程组其实就无唯一解了,如下:
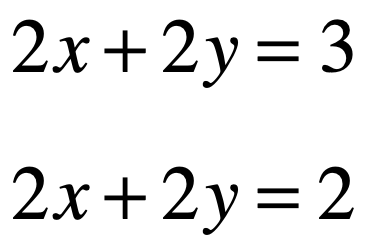
它的坐标上的直线是这样的:

三个未知数:
接下来看一下有三个未知数的方程,比如:
![]()
对于三维空间中满足上式子的所有点集合起来其实就是一个平面,如下:

那如果有两个三元方程组成一个方程组,如果两个平面相加的话可能是这样:

可以看到相交的部分组成了一条直线,而直线上有N多个点,也就是有无数解,所以当方程组个数小于未知数个数时,一定是没有唯一解,所以这就跟上面说的这种情况吻合了:
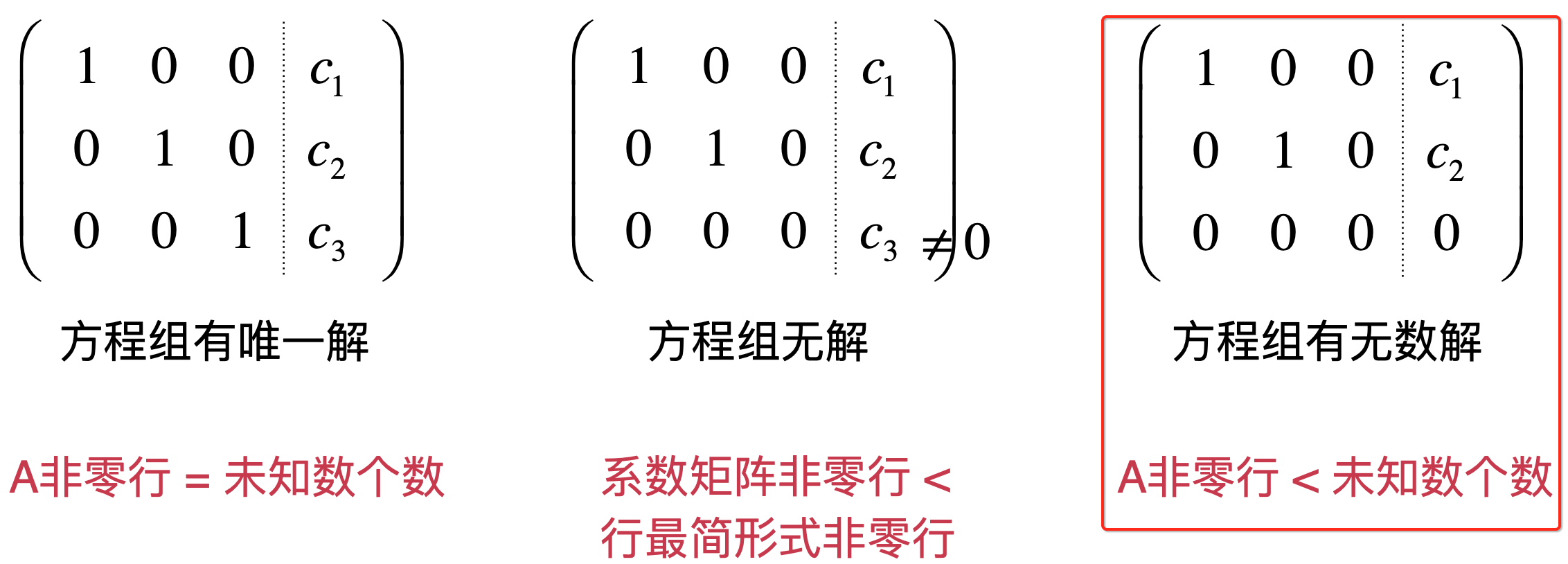
但是!!!也有可能无解,因为有可能两个平面不相交呀,比如像这样:
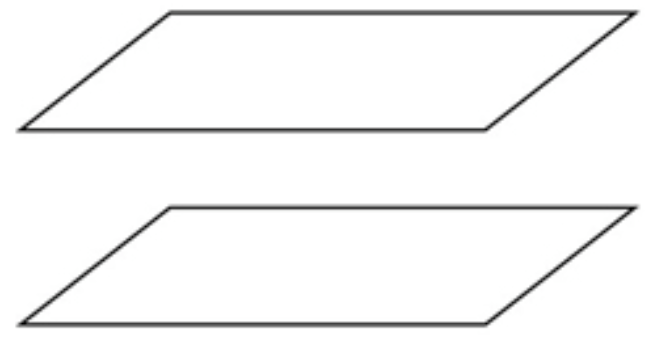
另外还有一个情况就是有三个三元方程组成的方程组,此时有可能是有唯一解,像这样:
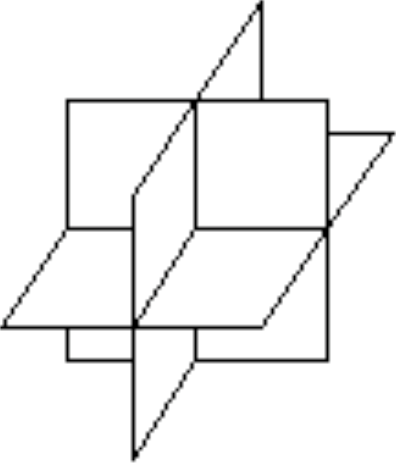
其中三个平面相交的点就是整个三元方程的唯一解。也有可能有无数解,像这样:

其中相交的是一条直线,有无数个点当然也就是无数个解喽。也有可能是没有解,像这样:

三个平面完全不相交,还有可能像这样:
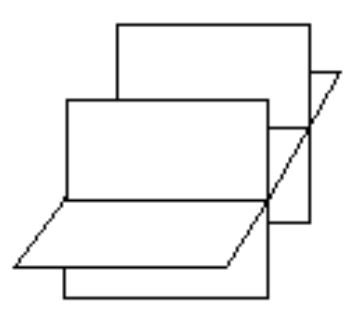
相加的位置是两条平行线,无法找到一个点同时在三个平面上。还有可能像这样:

四个未知数:
如果再升级,有四个未知数呢?就得要到四维空间上来想象了,这里看一下动图形象感受一下:

其中相交的是一个三角形,很显然是无解的,但是如果再将汇集成一个相交点其实也有一个唯一解的,这里也就是说明“对于n个未知数n个方程,才可能有唯一解”,其中唯一解是非常凑巧的情况,大概率也是没有解的。
三个二元方程:
这里再回到比较直观的二维视角来,比如有三个方程,但是只有二个未知数,在坐标点是两条连线,可能是这样:

此时对于第三个二元方程也是对应一个新的直线,可能是这样的:

其中这种情况肯定是无解的对吧,但是如果这样呢?

此时又有唯一解了,那有没有无数解的情况出现了,有:

所以此时针对这种情况又有个结论:“当方程个数多于未知数个数时,可能有唯一解,也有可能无解,也有可能有无数解”。
三种情况总结:
上面举例了这么多种情况,其实简单总结就是如下这张表:

有9种情况,但是此表以再进一步简化的,怎么简化呢?这里得回到行最简形式角度来看了,先看个结论:“对于行最简形式,系数矩阵的非零行不可能大于未知数个数”,比如:
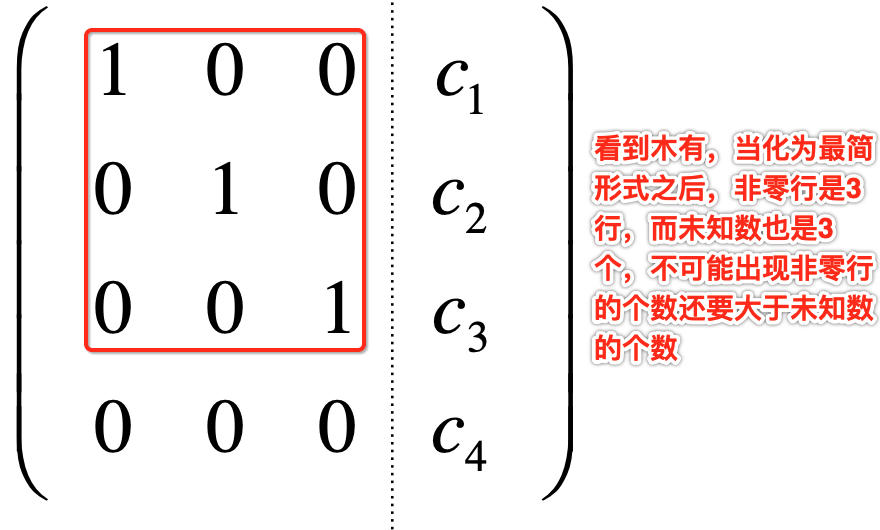
所以,上面9点情况可以改变为:

而对于无解的情况就是看看当化为最简形式之后有木有一行产生矛盾,所以先把无解的情况也去掉,只看木有矛盾的情况,进一步简化表格为:
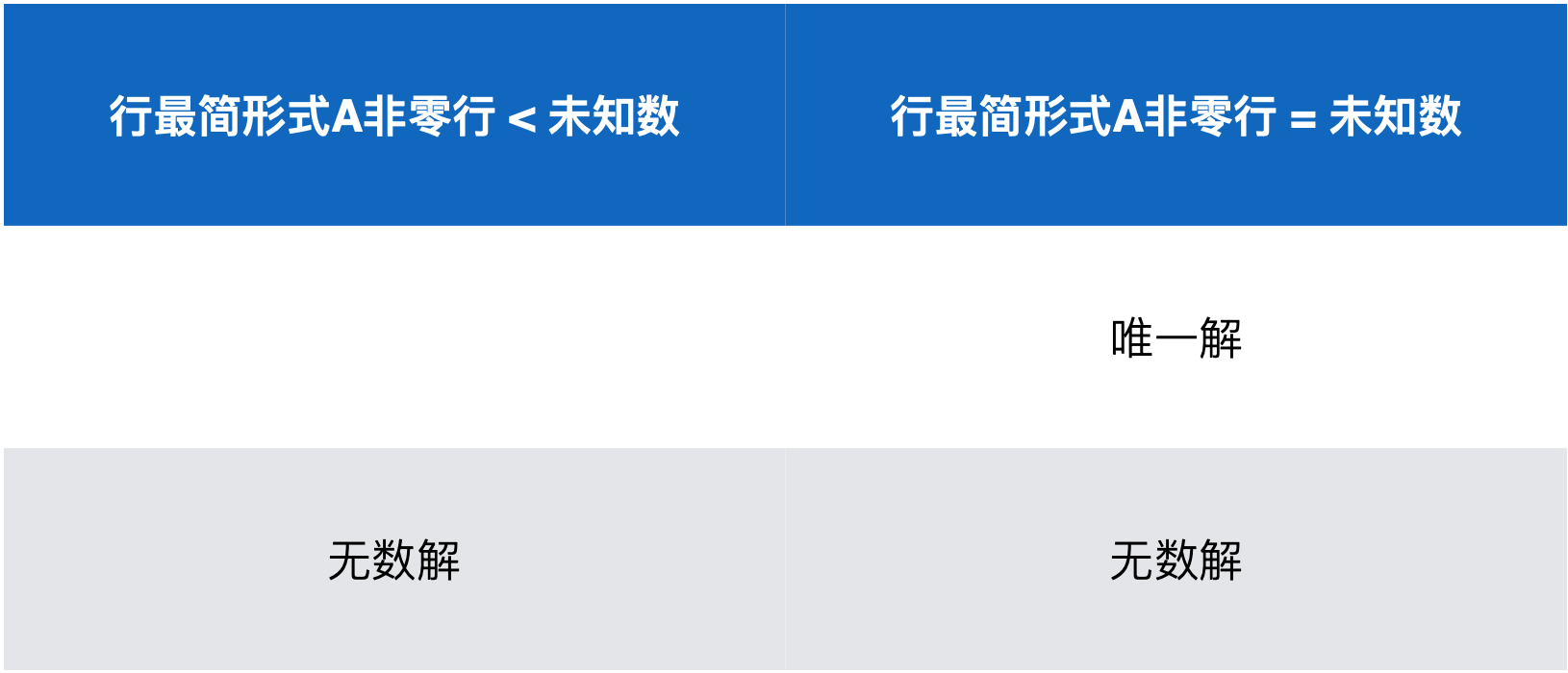
而当行最简形式非零行=未知数时:
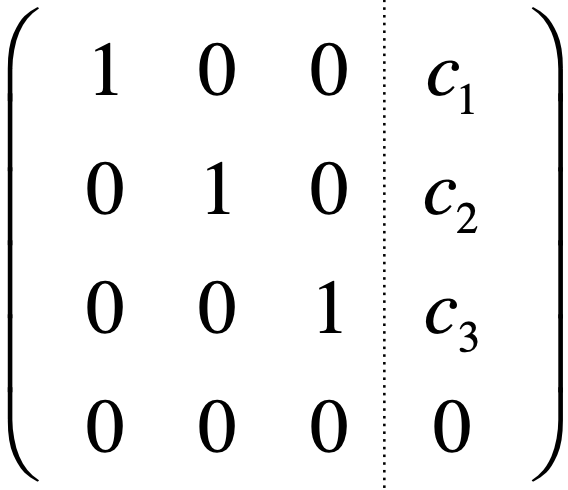
很明显只有可能是唯一解,因为只有方阵才可能满足非零行=未知数的个数,也就是说:“对于行最简形式,系数矩阵的非零行等于未知数个数时,一定有唯一解”,所以表格又可化简为:

而由于此时将有无解的情况去掉了,这里再将无解的也考虑进来,其所有的情况就为:

所以,经过这么一分析,对于一个方程组的解的结构的计算就变得比较简单了,首先判断是否无解,如果不是,则再看有解的情况是无数解还是唯一解。
更一般化的高斯-约旦消元法:
在上面学习线性系统求解时举的都是当通过高斯约旦消元法化为行最简形式后都是n个未知数n个方程增广矩阵进行求解的,那如果是方程的个数和未知数的个数不匹配时在具体使用高斯约束消元法时会出现什么样的问题,又该如何处理呢?
这里先来回忆一下高斯消元的过程,分为两步骤:

而此次咱们探讨的是方程的个数跟未知数的个数不匹配的情况,依然要严格遵守上面这个过程才行,下面看个具体例子:

它对应的增广矩阵为:

首先找到第一个主元:
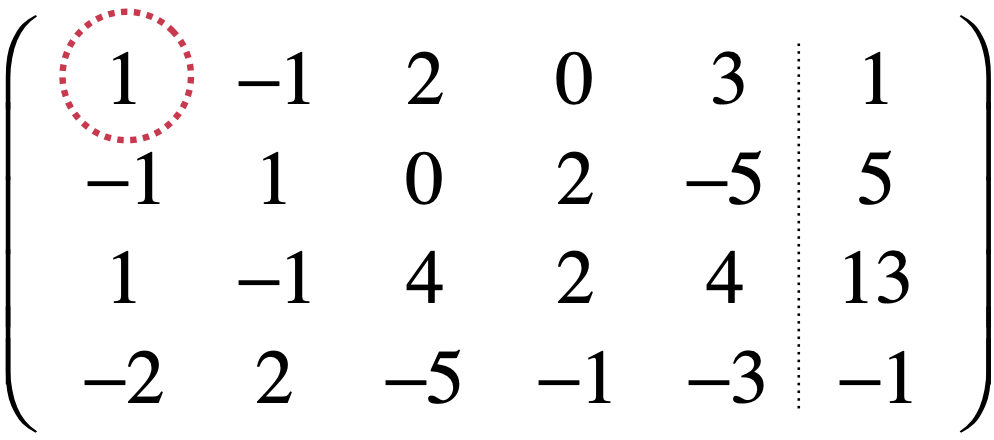
已经是1了就不需要将其归一了,然后接下来则就是将它下面的元素归0,很简单,只需要让第二行+第一行、第三行-第一行、第四行+第一行*2既可,变为:

此时发现居然它下面的第二行也都为0了,所以找第二行主元时发现第二列元素为0之后则往后列再找非0的既可,此时找到的是2将其当作主元:

由于主元不是1,先将其归1,直接当第二行/2变化为:
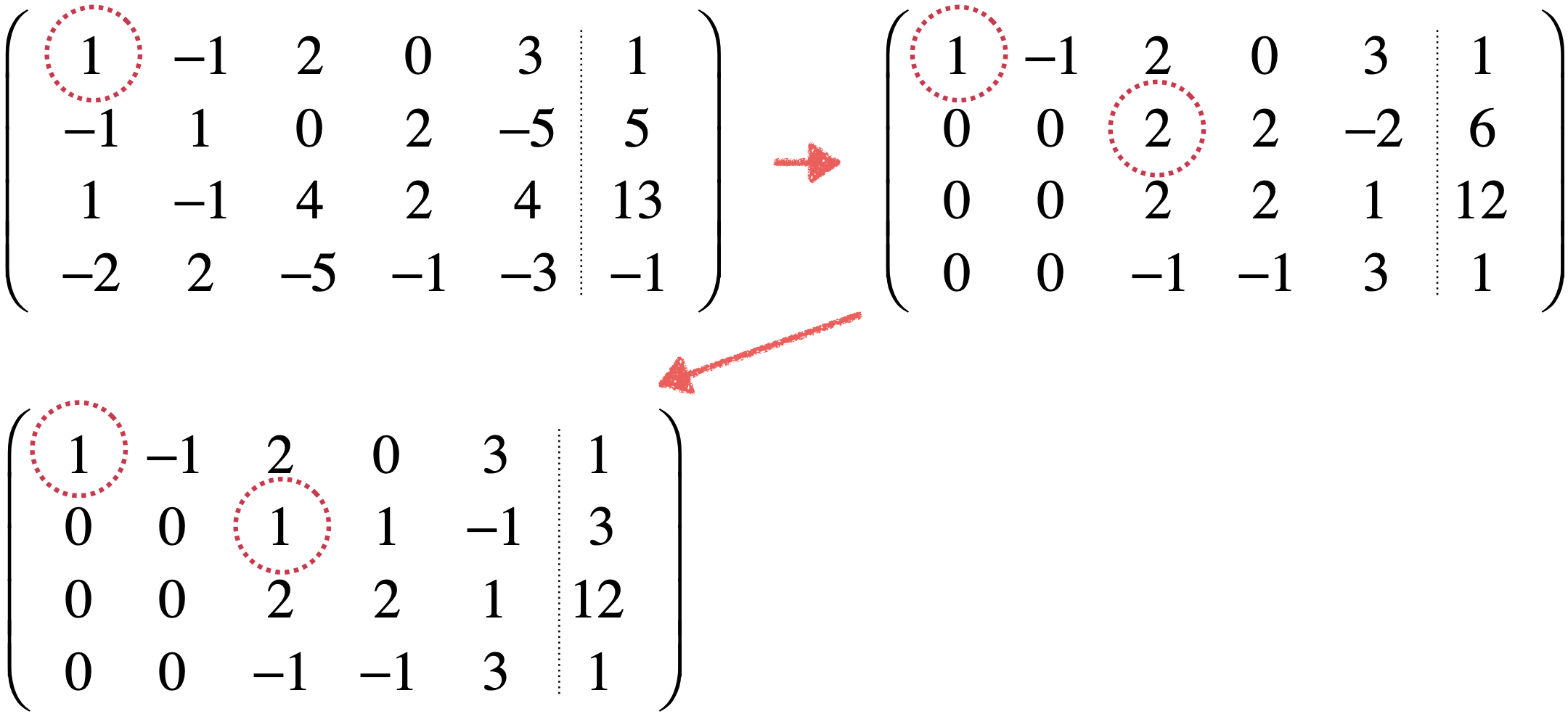
然后再将它下面的元素归为0,这里具体就不算了,直接给出结果:

此时发现第四列下面也都为0了,同样的第三的主元则又找非0元素,此时就为3了:

此时主元不为1,先归一,然后再将下面的归0,整体为:

以上就是高斯消元的过程,接下来则需要后向过程了,将主元之上的元素也都归0,整体为:
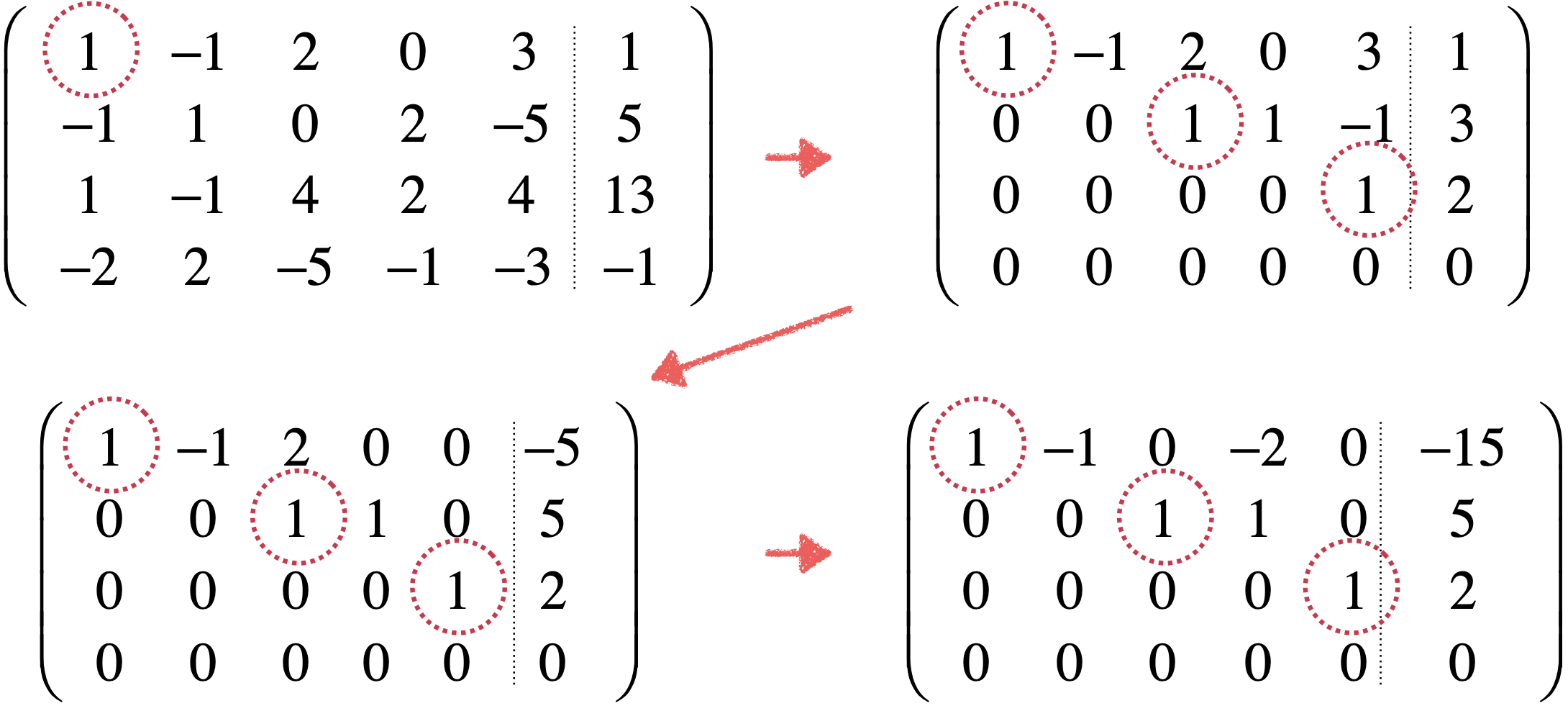
此时对于方程组就已经化为行最简形式了,如下:

很明显该方程是有解的,因为行最简形式的系数矩阵的非零行是3行,小于未知数,当然有无数解喽。
而行最简形式对应的方程组的样子就为:

它又可以变化为:
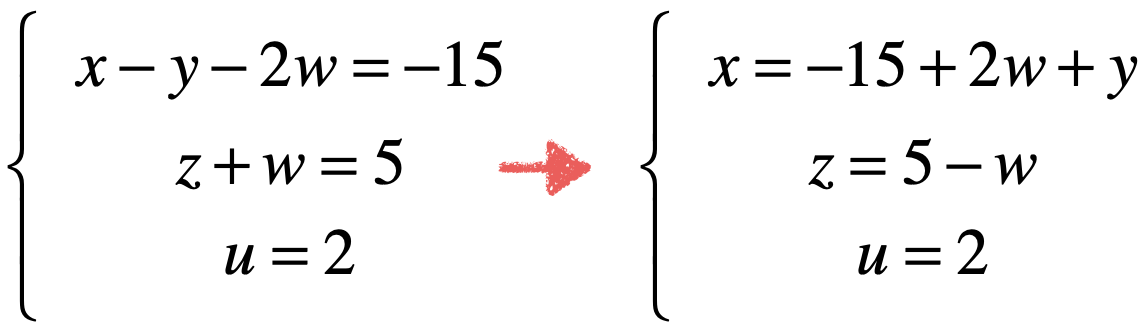
其中x,z,u其实就是表示主元,对于有主元的列可以称之为:

而对于没有主元的列可以称之为:

有了这个定义之后,是不是发现:

x,z,u表示主元,它是等号右边是由结果元素和自由列进行操作运算,上面这式子再变换一下可能更加的清晰,如下:

而其中y、w可以有无数个值,所以整个线性系统是有无数个解的。而举这个例子跟之前不同的主元并非是在n行n列了,而且通过这个视角对于一个线性系统也很容易写出它的解的式子了。
下面再来看一个特殊的线性方程系统,方程个数>方程未知个数:
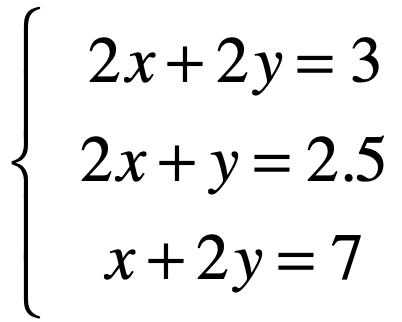
它对应的增广矩阵为:
然后先进行前向的高斯消元过程,过程直接略过,因为已经对整个消元的过程非常熟悉了,结果如下:

其中出现了矛盾的第三行,一看就是无解了,也就没必要进行后向过程了。
实现更一般化的高斯-约旦消元法:
接下来回到python的世界,来实现高斯约旦消元的过程:
去掉nxn方程的断言:
由于之前咱们只考虑了nxn的系统矩阵:

而这里肯定是没有这个限制了,因为对于nxm的矩阵依然是可以进行求解的,所以先去掉:

增加主元列的存储变量:
由于对于更一般的线性系统而言,主元列并非是n行n列,而对于这种系统的求解对于主元列在哪是非常重要的,所以定义一下变量专门存储主元列的信息,如下:

其中将其也定义pulic的,因为之后可能在外面会直接用到它。
_forward()逻辑修改:
对于原来前向过程的实现回忆一下:
由于此时已经不是nxn的方阵了,所以对于前向的过程逻辑也得进行重新修改了:
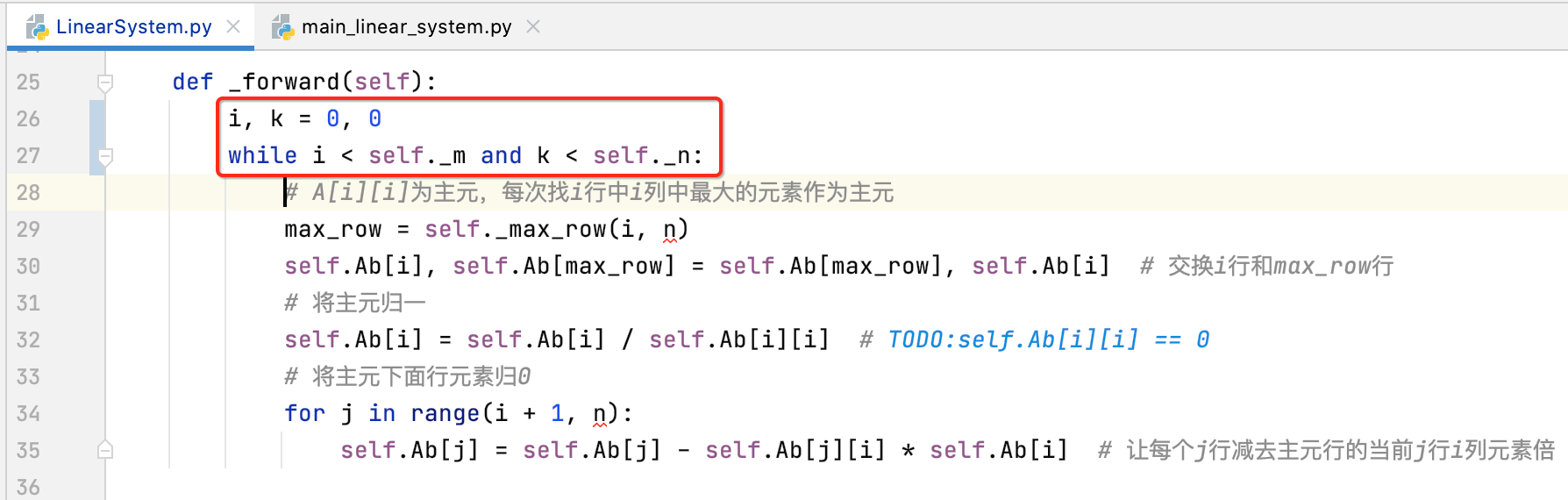
此时需要判断Ab[i][k]是否是主元,因为如今主元的位置并非是n行n列了:

此时就需要修改_max_row()寻找主元位置的逻辑了:
而它里面的实现逻辑基本不用变,就替换下新的参数既可,如下:

回到主流程继续往下改:


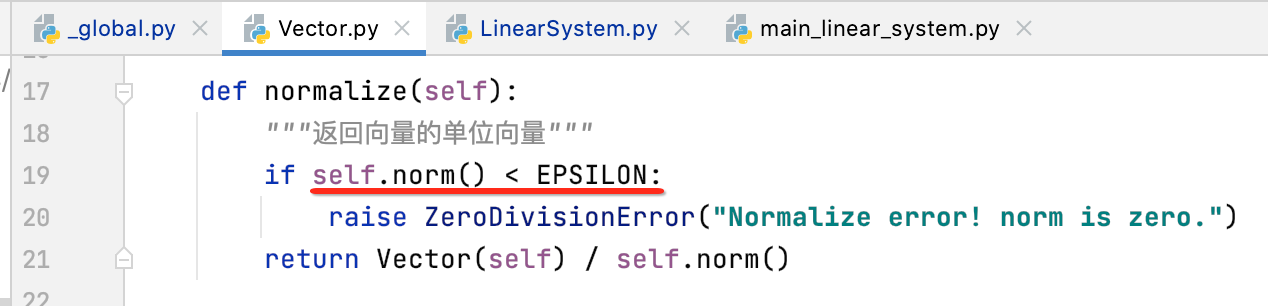
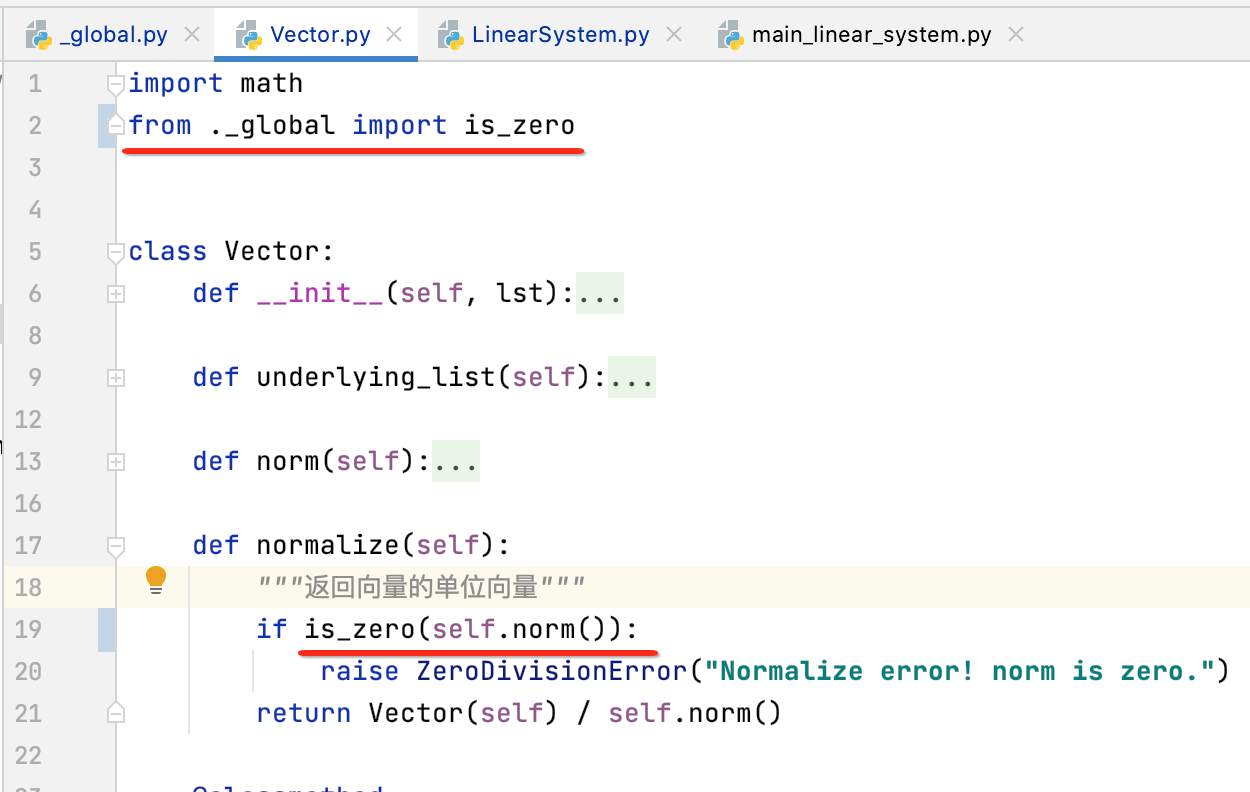
其中对于判断浮点式是否等于0在这块封装了两个方法供以后的调用方便:
这样对于原来Vector中判断浮点式是否为0就可以使用该方法了,如下:
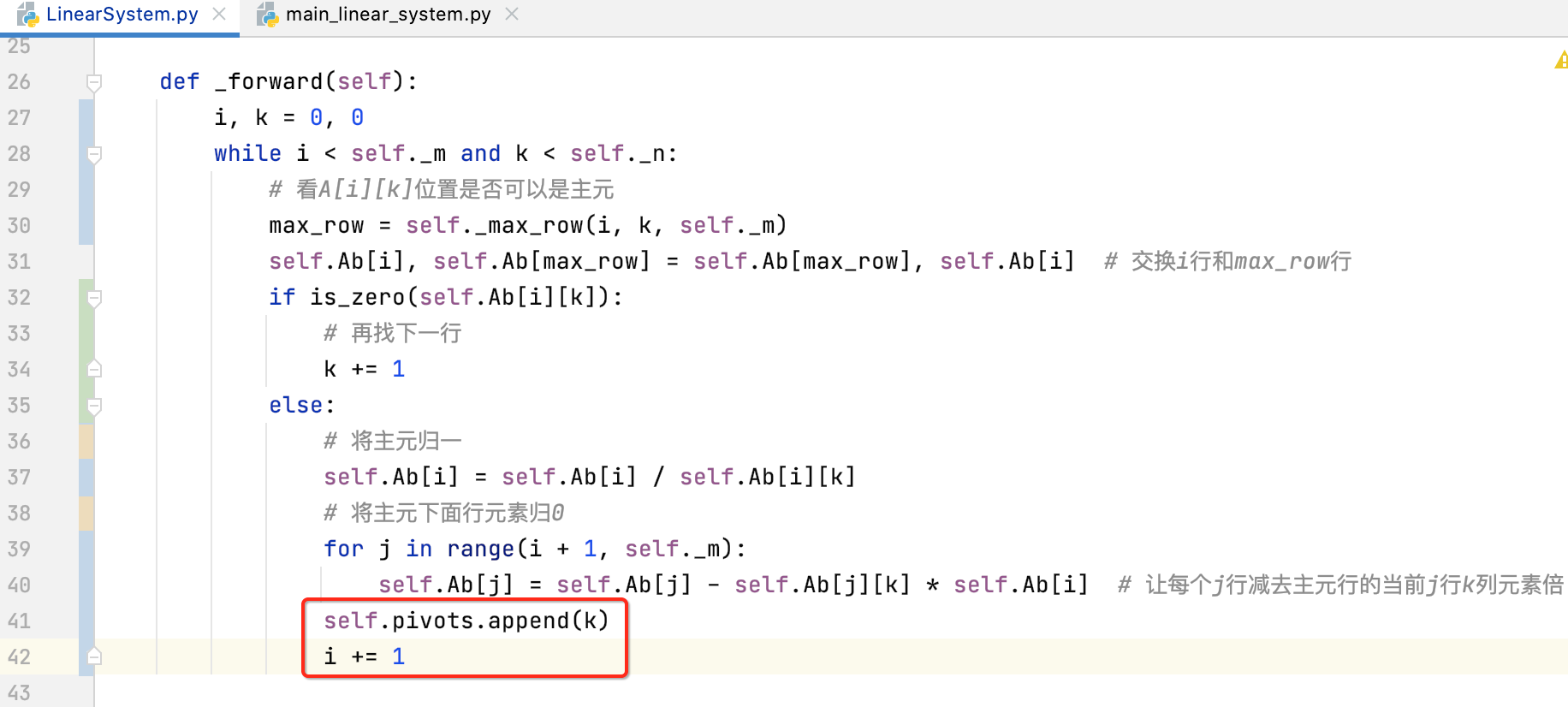
最后记得要记录一下主元列到变量当中,如下:
_backward()逻辑修改:
有了前向过程的修改思路,对于后项过程的修改就比较简单了,先来回忆一下目前的实现:

也是由于不是nxn的系数矩阵了,所以修改如下:

测试:
先来看一下原来咱们的测试用例好不好使:
from playLA.LinearSystem import LinearSystem from playLA.Vector import Vector from playLA.Matrix import Matrix if __name__ == "__main__": A = Matrix([[1, 2, 4], [3, 7, 2], [2, 3, 3]]) b = Vector([7, -11, 1]) ls = LinearSystem(A, b) ls.gauss_jordan_elimination() ls.fancy_print() print() A2 = Matrix([[1, -3, 5], [2, -1, -3], [3, 1, 4]]) b2 = Vector([-9, 19, -13]) ls2 = LinearSystem(A2, b2) ls2.gauss_jordan_elimination() ls2.fancy_print() print() A3 = Matrix([[1, 2, -2], [2, -3, 1], [3, -1, 3]]) b3 = Vector([6, -10, -16]) ls3 = LinearSystem(A3, b3) ls3.gauss_jordan_elimination() ls3.fancy_print() print() A4 = Matrix([[3, 1, -2], [5, -3, 10], [7, 4, 16]]) b4 = Vector([4, 32, 13]) ls4 = LinearSystem(A4, b4) ls4.gauss_jordan_elimination() ls4.fancy_print() print() A5 = Matrix([[6, -3, 2], [5, 1, 12], [8, 5, 1]]) b5 = Vector([31, 36, 11]) ls5 = LinearSystem(A5, b5) ls5.gauss_jordan_elimination() ls5.fancy_print() print() A6 = Matrix([[1, 1, 1], [1, -1, -1], [2, 1, 5]]) b6 = Vector([3, -1, 8]) ls6 = LinearSystem(A6, b6) ls6.gauss_jordan_elimination() ls6.fancy_print() print()
运行结果:
/Users/xiongwei/opt/anaconda3/bin/python3.8 /Users/xiongwei/Documents/workspace/python/Play-with-Linear-Algebra/LinearAlgebra/main_linear_system.py 1.0 0.0 0.0 | -1.0 -0.0 1.0 0.0 | -2.0 -0.0 -0.0 1.0 | 3.0 1.0 0.0 0.0 | 1.9999999999999996 -0.0 1.0 0.0 | -3.0000000000000018 0.0 0.0 1.0 | -3.9999999999999996 1.0 0.0 0.0 | -1.9999999999999998 0.0 1.0 0.0 | 1.0 -0.0 -0.0 1.0 | -3.0 1.0 0.0 0.0 | 2.9999999999999996 -0.0 1.0 0.0 | -3.9999999999999996 0.0 0.0 1.0 | 0.4999999999999999 1.0 0.0 0.0 | 3.0 -0.0 1.0 0.0 | -3.0 -0.0 -0.0 1.0 | 2.0 1.0 0.0 0.0 | 1.0 0.0 1.0 0.0 | 1.0 -0.0 -0.0 1.0 | 1.0 Process finished with exit code 0
接下来再来新添加一些特殊的测试用例:
A7 = Matrix([[1, -1, 2, 0, 3], [-1, 1, 0, 2, -5], [1, -1, 4, 2, 4], [-2, 2, -5, -1, -3]]) b7 = Vector([1, 5, 13, -1]) ls7 = LinearSystem(A7, b7) ls7.gauss_jordan_elimination() ls7.fancy_print() print()
运行:

其实也就是上面理论描述的这个结果:

下面再来增加一个测试用例,如之前所述的:

如下:
A8 = Matrix([[2, 2], [2, 1], [1, 2]]) b8 = Vector([3, 2.5, 7]) ls8 = LinearSystem(A8, b8) ls8.gauss_jordan_elimination() ls8.fancy_print() print()
运行结果:

不过为了看出有解无解,这里对于高斯约旦消元方法增加一个返回值,如下:
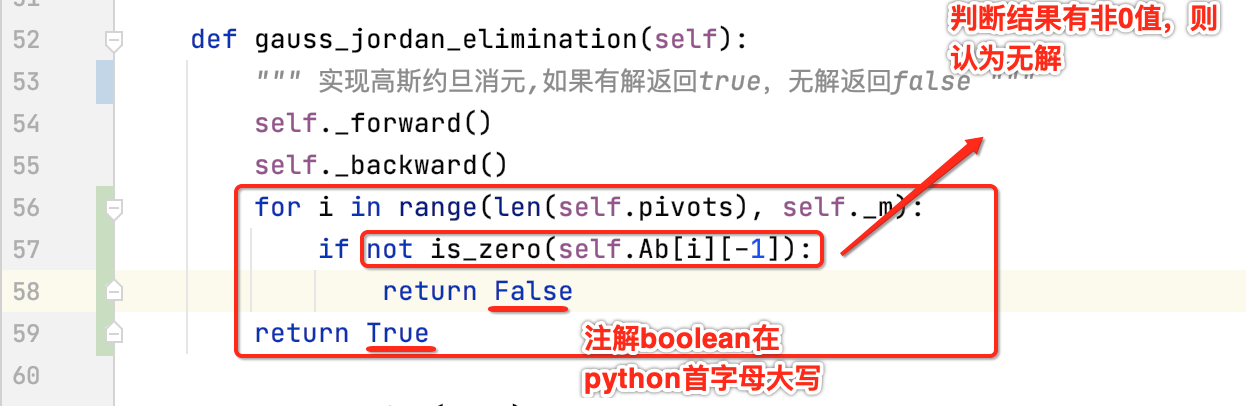
下面修改下测试用例:
b8 = Vector([3, 2.5, 7]) ls8 = LinearSystem(A8, b8) if not ls8.gauss_jordan_elimination(): print("No Solution!") ls8.fancy_print() print() A9 = Matrix([[2, 0, 1], [-1, -1, -2], [-3, 0, 1]]) b9 = Vector([1, 0, 0]) ls9 = LinearSystem(A9, b9) if not ls9.gauss_jordan_elimination(): print("No Solution!") ls9.fancy_print() print()
运行:

其中最后一种情况知道为啥木有解了不,因为很显然非0行其实是2行,而未知数是3个,另外最后一行的结果是一个非0。
齐次线性方程组:
在最后再来学习一个概念,如标题所示:齐次线性方程组,那它是个什么东东呢?其实下面这种方程组就是:
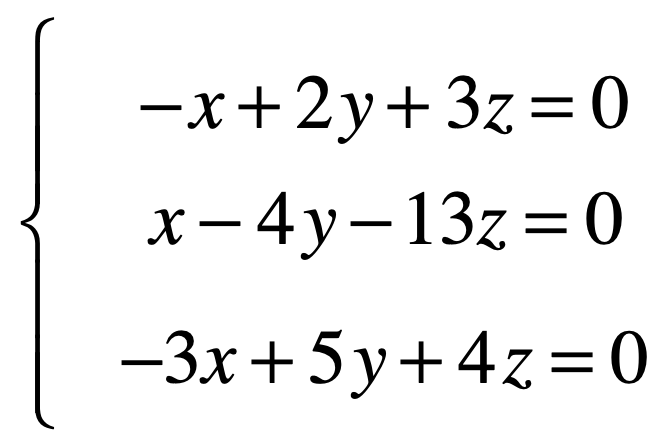
也就是方程组的每一个结果都为0,而求解过程跟普通方程的求解是一样的,如下:

但是!!它有一个特点,对于这样的方式是肯定有解的,因为至少有一个解是让所有未知数取0对不?而也有可能它是一个解还是无数解,依然还是根据之前的判断规则来,如上方程很明显有无数解,因为非0行是2,而未知数是3。
既然它最后一列肯定永远为零,那么咱们就不需要使用增广矩阵了,在求解的过程中直接对系数矩阵进行操作既可,如下:
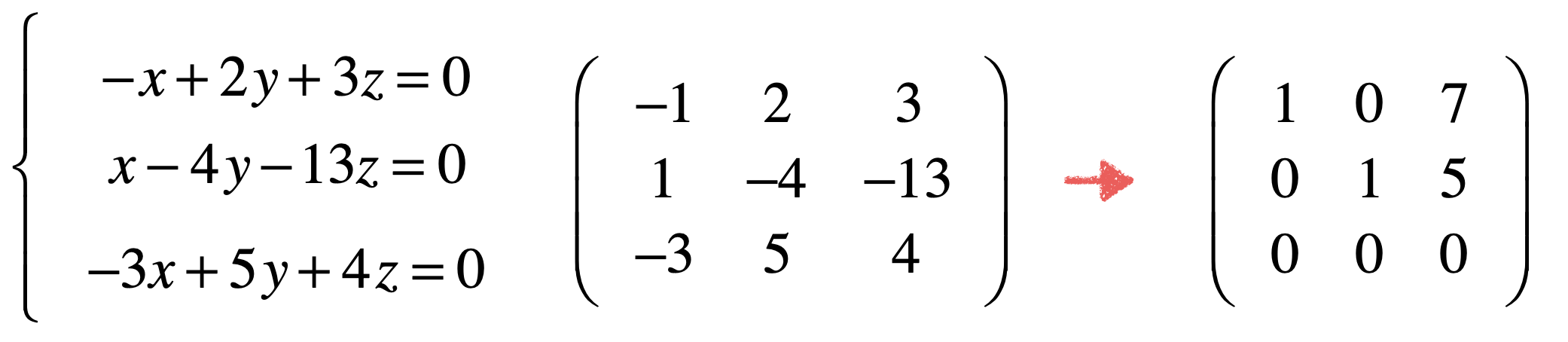
其中它也是满足行最简形式的对不?同样也可以用之前所学的方式来判断方程组的解的形式。所以总的而言先了解齐次与非齐次的区别:

那了解这个概念有啥用呢?因为在线性代数中对于齐次线性方程组它特殊的性质会在未来的学习中起到一定的作用,比如之后的空间的学习。