前言:
从今天起开启一门新课程的学习,如标题所示那就是大学的数学课本之一----线性代数,为什么要学它呢?因为这周收到领导的技能考核通知【每年一次,超恶心的】,当时收到这消息真是万马奔腾。。还要向高考一样把你给考倒不成不~~更何况对于学渣都不是的我只对“线性代数”这四个名词有印象,而对于它里面的内容全都交还给了老师,这块准一考一个倒。当然无它法喽,恶补,另外其实跟自己内心的学习计划刚好相撞了,上个月本身就想把数学、英语给系统的再学一遍,毕竟对于程序猿职业为生的我们这俩基本功还是非常重要的,所以从另一个角度来想其实还得感谢公司能让这块的学习提前提上日程了。根据我的学习格言:“好记性不如烂笔头”这一点,当然有必要详细记录起整个这块的学习历程,为未来的再次复习打下良好的基础。当然这块的学习也会比较枯燥,毕竟不像做应用开发那样有趣,所以拥有“恒心”非常重要!!!
概述:
线性代数是高等教育中理工科学生必学的数学,毫不夸张的说,线性代数是近现代科学发展过程中最重要的基础数学之一,为啥这么重要呢?这里可以先从初等教育中(小学、初中)说起,在那个阶段的代数更多的是在研究一个“数”,而数可以分为如下三种:
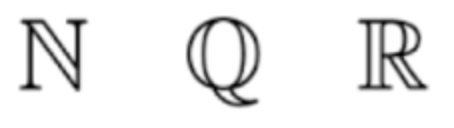
N表示自然数;Q表示有理数、R表示实数。进而当时研究的一个重要的课题就是函数:
![]()
而函数其实就是传入一个数,得到另一个数对吧?都是一个数。
而到了线性代数则对上面初等的代数进行了拓展,它主要是研究“一组数”,也就是一个空间,既向量(Vector,下面就会学到),所以它的类型就会为:
![]()
同时研究的课程也是函数,只不过此时的函数研究的对象是向量了,如下:
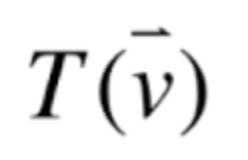
而一谈到线性代数可能大伙的第一反应就会想到矩阵,其实它可以理解成对于一个向量进行变换的一个函数,待之后学到再说。
从研究一个数升级到一组数:
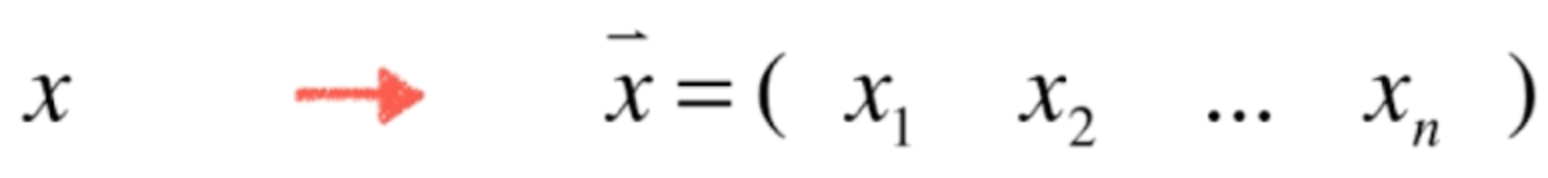
其原因是因为:
- 真实的世界是多维度的;
- 单变量不足以描述真实世界;
- 用单变量描述真实世界是不方便的;
这也是近乎所有的理工科教材中,都充斥着线性代数的公式或者符号,而线性代数可以用到的场景也非常之多: 计算机、人工智能、经济、建筑、地质、宇宙、化学...。
一句话,有时间有经历,学好它,对于自己程序员的职业发展只有利无一害的,先啰嗦到这,下面正式开启线性代数的学习大门~~
从向量起开启学习之路:
什么是向量?
在上面的概述中也说明了为啥线性代数这么重要,是因为真实世界是多维度的,所以需要从研究一个数拓展到研究一组数上来,而一组数的基于表示方法就是向量(Vector)。
1、向量(Vector)是线性代数研究的基本元素。比如:
一个数可以是666;而一组数可以是(6, 66, 666);
2、一组数有啥用?
既然向量是表示的一组数,那这组数有啥用呢?其实最早的出发点是用来表示方向用的,也正是因为这个原因,中文翻译Vector叫“向”量。比如说在一个二维的平面中,从一点到另外一点可以画这么个箭头:

假设起始点到终止点的距离是5000m,很可能起始点是一样,但是其终止点不一样对么?比如:

所以如果只用5km这个数字来表示最终走到了哪里是远远不够的,此时向量就可以更有意义了,咱们可以针对上面的绘制一个二维的坐标轴,如下:
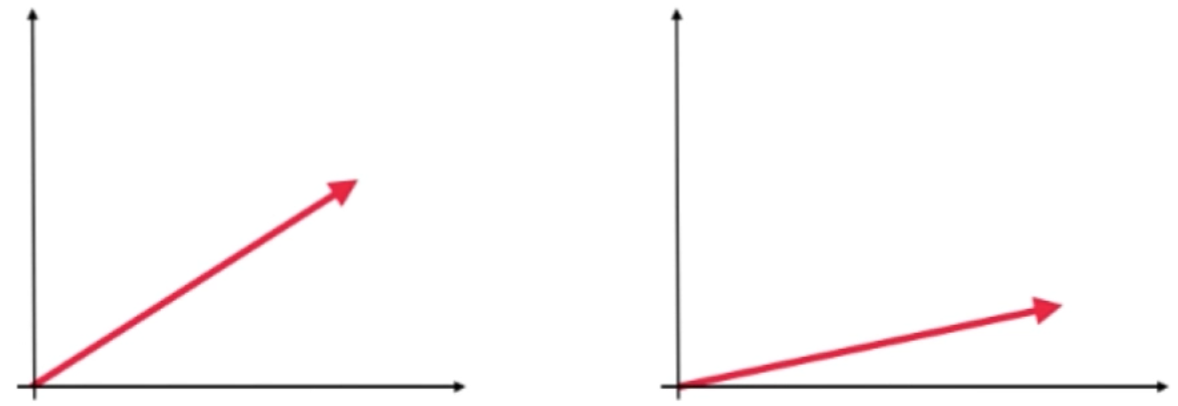
其中就可以看到x轴和y轴的数值情况了,如下:
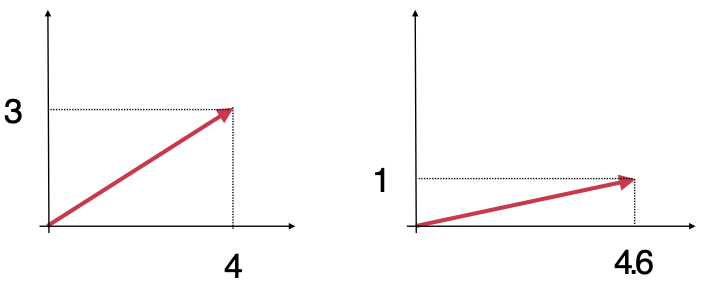
左边的x轴走了4km,y轴走了3km;右边的x轴走了4.6km,y轴走了1km。所以同样走了5km,而终点的位置却是不同的,可以用这个坐标来表示一下终点:
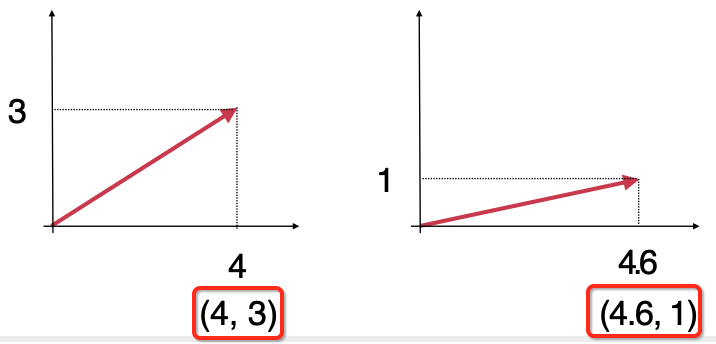
同样的对于三维空间也是一样的,同样走5km,但是由于方向不同最终落到三维空间中的坐标也会是不一样的:
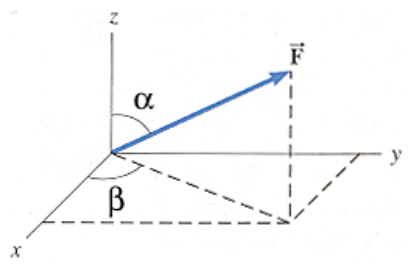
上面这个例子对应物理学中的位移,其实像速度、加速度、力这样的物理量都是具有方向这样的概念的。
在上面这个例子中咱们只考虑了方向,但是都木有来考虑起始点【目前这例子的起始点是在(0,0)的坐标上】,难道起始点不重要么?其实在向量这个世界的研究中确实是不重要,比如像这样的起点:
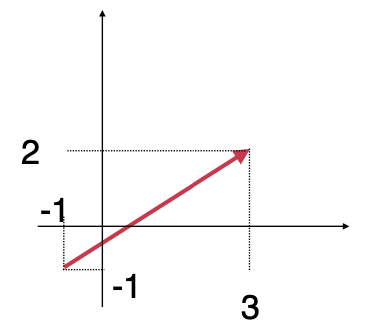
它表示是从(-1,-1)这个起始点走到了(3,2),也是在x轴上走了4km,y轴上走了3km,在线性代数这个世界中它和从(0,0)到(4,3)其实是一样的,这俩之间其实就是坐标系不同,
3、向量是一组有序的数:
对于向量来说,它只表示从一个点到另外一个点相应的结果,而不区分从哪个点出发的,所以为了研究方便,我们定义向量都从原点起始,但是!!!由于向量是由多个数字来表示的,数字之间的顺序是重要的,比如:
(4,3)和(3,4)这俩表示的向量的意义就截然不同。
4、更加抽象的:n维向量
在上面说明为啥要引入向量这个概念,也就是要用一组数来表达世界中的一些事务,正是因为具有方向这个概念,但是!!!如果只是用来表达物理中的方向这个概念的话,其实只要三个维度就够了,因为在人类的感知中世界是一个三维空间,任何有形的方向最多只能在三维的空间中,但是!!!为了拓大我们研究的范围,也是增强向量这个数学概念它的能力,可以上升到n维向量。而在现实中用高维的空间来表达一个事物也是比较常见的,比如描述一个房子的情况:

此时就使用了一个5个维度的向量(120, 3, 2, 2, 666),此时,向量量就是一组数,这组数的含义由使⽤者定义。
5、两个视角:
目前貌似对于向量就有两种视角了,如下:
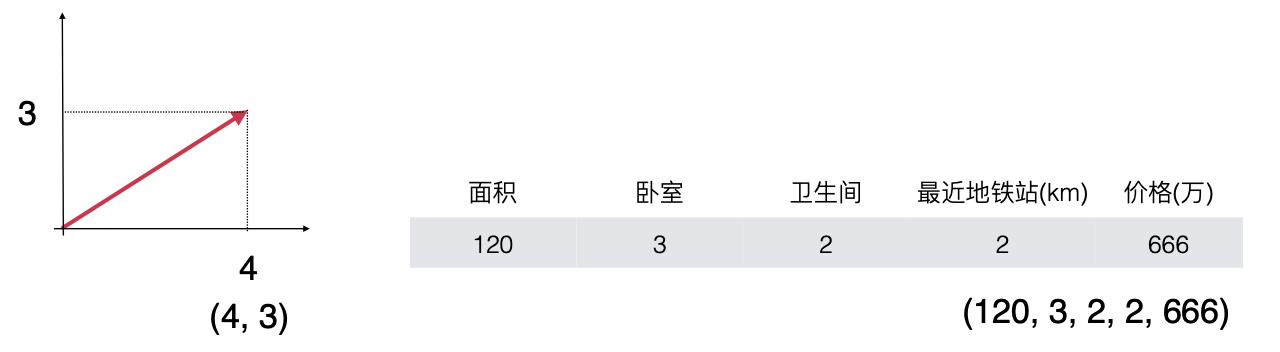
左图的向量是以方向的视角来看待的,而右边的仅仅是一组有序的数字。两个视角看似不同,但是可以互相转换的,下面来看一下如何转换:
a、左图是以方向的视角来看待的对吧,其实它也可以看成是二维空间中的一个点(4,3),是不是就变成右图的视角了?
b、右图是以一组有序的数字的视角来看待的对吧,不是表示一个方向,对于这一组有序的数字其实可以看成是在高维空间中的一个数据点,换言之,对于这个五维向量可以想象成有一个拥有五个维度坐标轴的空间,每一个维度的坐标取值都可以从负无穷到正无穷中任意取值,对于当前房子的数据就可以对应这5个维度分别取这些值所对应的一个点。而空间中的任何一个点,可以看做从原点指向这个点的一个⽅向,是不是就变成了左边视角了?
在实际使用线性代数过程中,更倾向于使用右边这个视角来看待向量,也就是把每个向量看成是空间中的一个点,但是!!!在学习初期,使用方向的视角,会更直观,更形象,因为可以直接在二维的空间中直接绘制出来比较直观。
不管怎样,对上以上两个视角要明白,它们都不是简单的“一组数”。对于第一个视角来说向量是有方向的是因为是我们把它看成了一个有向的线段,而对于第二个视角是看成了空间中的一个点,这俩个视角都有一定的几何意义,而不仅仅是数学上的数字堆叠而已,这点有一个了解。
向量的更多术语和表示法:
- 和向量相对应的一个数字称为“标量”
这是针对初中代数研究的是一个数而言的。 - 代数,⽤用符号代表数
“线性代数”中的代数,为了和标量进行区别【标量是直接用某个数字来表达】,会用符号代表数,所以对于向量而言它的符号画箭头为它:
也就是在V上面多了一个箭头,说明这不仅仅只表示一个数字。 - 个别情况下,我们会考虑向量的起始点
呃,这个不是跟之前描述的矛盾了么?还记得之前说了啥么?回忆一下:

对于这样一个向量:

而如果考虑起始点的话,则会:
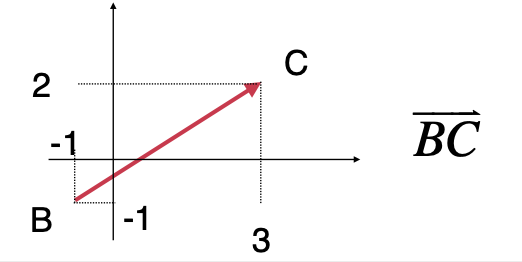
这是因为在研究几何学时会考虑起始点,从线性代数的角度其实这俩还是一样的。
-
行向量和列向量:
其实很好理解,就是表示方法的问题:
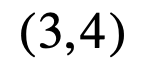
它就是行向量,也就是将向量码成一行,而列向量就长这样:
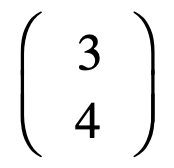
在目前学习向量阶段其实这俩没啥区别,但是!!!在后续要学到矩阵的时候就不一样的,到时再说。而通常教材、论文提到的向量都是指列向量,而由于横版印刷原因,如果采用这种列向量的方式不便于排版,所以会使用这样的符号代替:
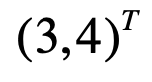
其中T是转置的意思。
实现属于我们自己的向量:
环境搭建:
接下来则编程来使用一下向量,这里使用python来进行编写,关于python这块我是纯小白,但是也不影响我继续学习的前进之路,我只要按照课程将它运行起来不影响程序的运行既可,至于python的语法不知道也无关系,先跑起来再说,之后有时间再来研究这门语言,这其实也是一种比较快速的学习方式,先跟着照猫画虎,不影响整个课程的学习,而对于一个完全陌生的技能在抄作业时会有N多个为什么,都放到之后的研究当中去,因为已经在大脑中已经有对于这门新技术的大致印象之后,这样也能激发自己想进一步学习它的欲望。
安装anaconda:
既然要使用python,当然电脑上先要安装一下它的环境,这里选择通过anaconda来安装,先来了解一下它:

看到木有,数据科学软件包,装上它在未来机器学习也可以派上用场的,用起来,先来上官网https://anaconda.org/下载:

点击下载安装既可,

其安装过程一路下一步既可,这里就不多说了。安装完之后打开,对它简要的了解一下,可以看到首页集成的一些工具集:

不过这里主要是看它给咱们安装的python的环境:

另外它还可以创建一个python的虚拟环境:
反正安装保持默认,此时咱们的Python环境就已经有了。
使用PyCharm CE:
而对于Python代码编写的IDE,还是选用jetbrains全家桶中的一员----PyCharm,直接上官网进行下载:
其中可以看到如今官网也对今年苹果推出自主研发的M1 CPU进行了兼容了:
然后打开创建项目:
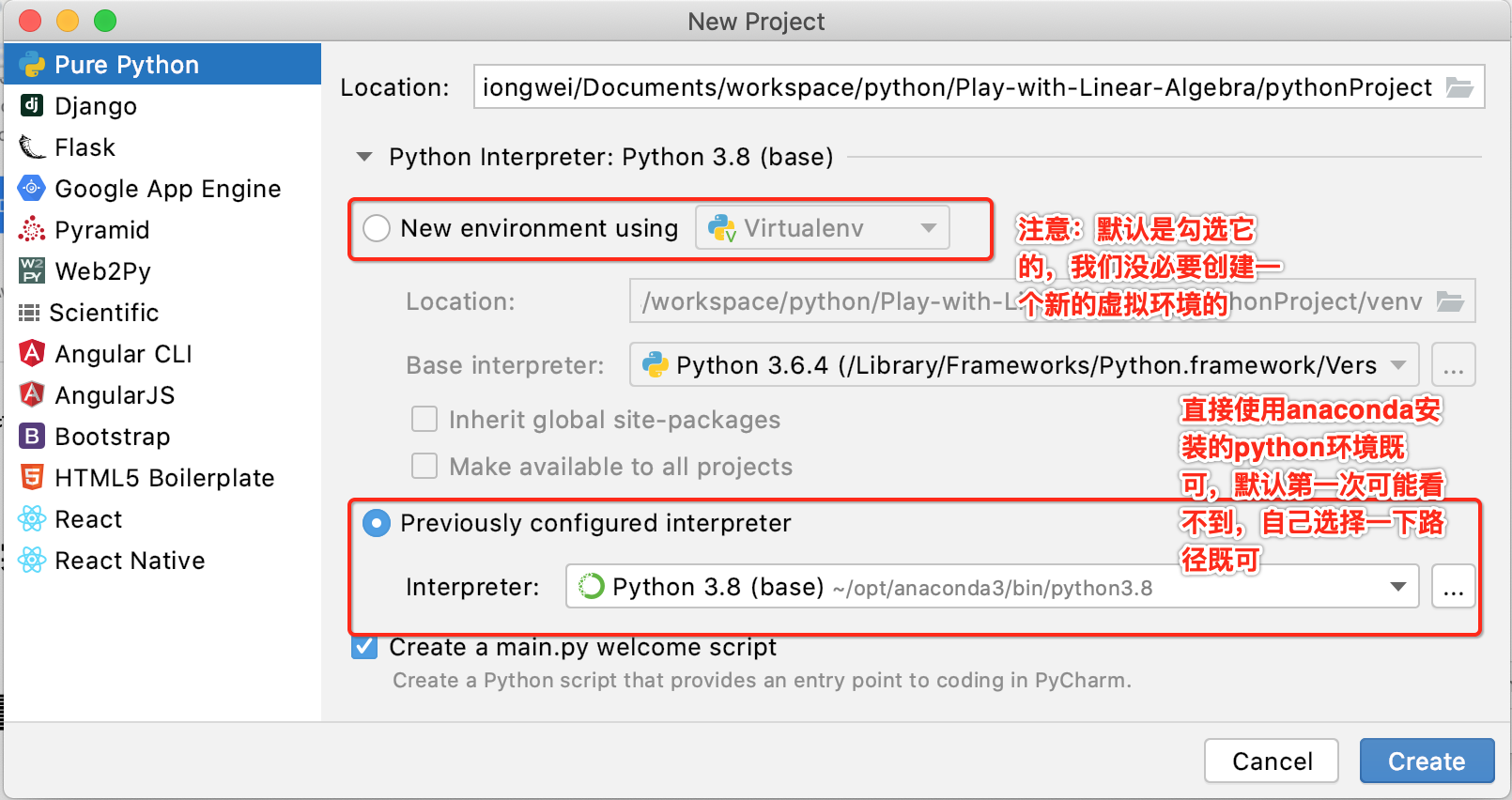
点击创建:
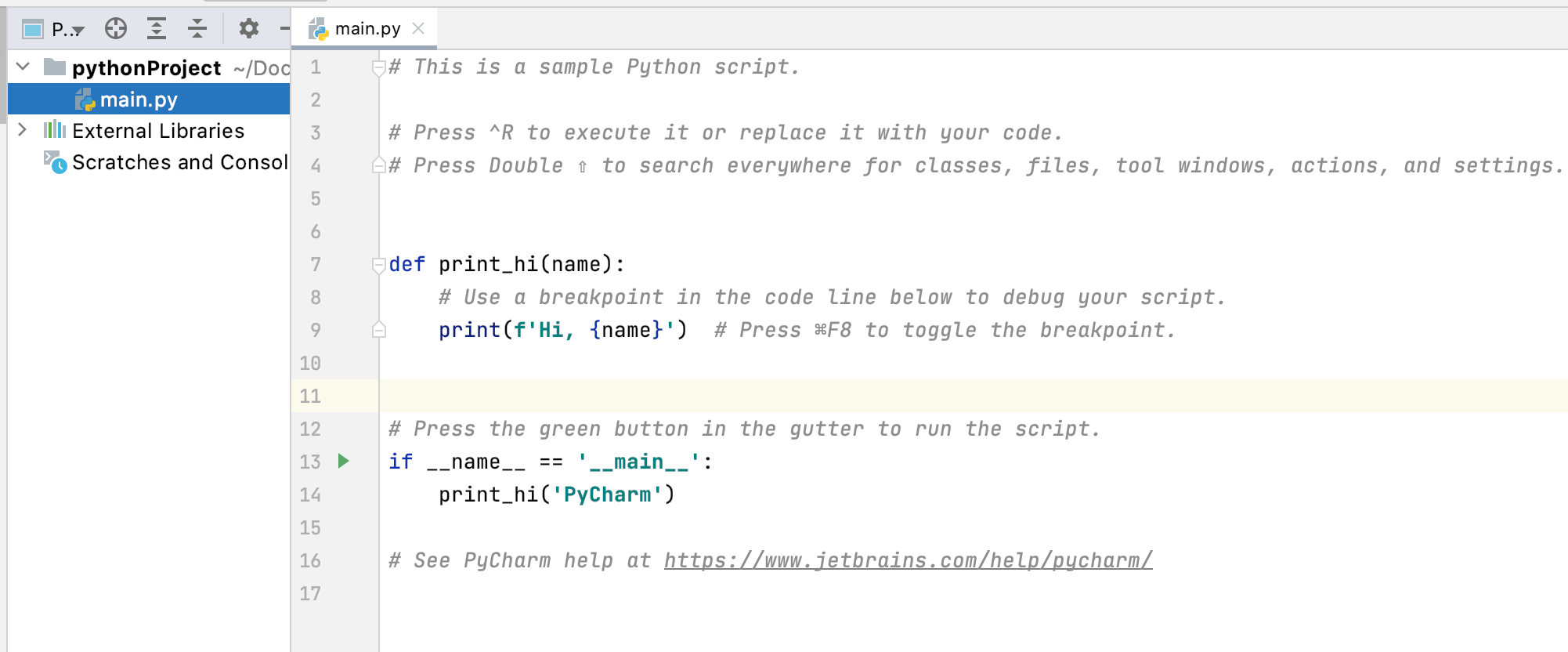
里面默认了一个HelloWorld级别的代码,能正常运行说明Python环境就ok:
不过咱们要来验证一下anaconda环境有木有安装正确,主要是在之后线性代数学习中会用到的两个数学包,如下:
import numpy import scipy import sys if __name__ == '__main__': print(numpy.__version__) print(scipy.__version__) print(sys.version)
运行:
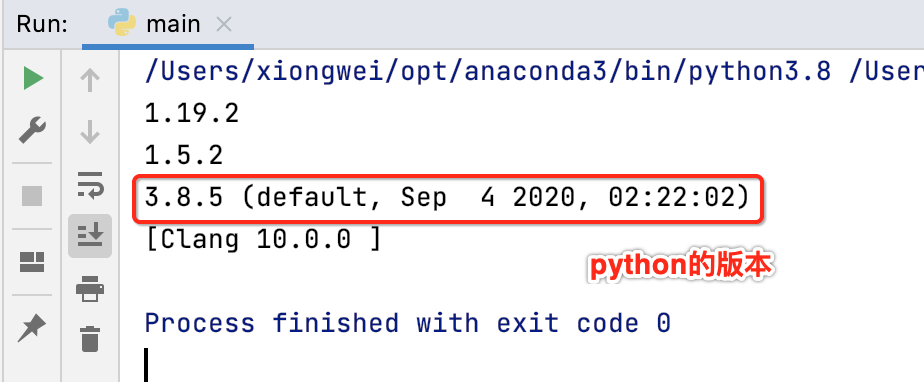
其中numpy、scipy是啥呢? 这里wiki一下:
至于它们的使用在之后的学习中再慢慢了解,至此对于咱们学习的编码环境就已经正式搭建好啦,接下来就可以撸码来实现咱们所学的向量了,接下来会有一大波陌生的python语法,莫要太在意,直接跟着敲起来就ok。
具体实现:
1、新建工程:

2、新建包:

这里不问为什么,因为这里不是来研究Python语法的,重点是能编写出来代码验证咱们的线性代数的学习就成。
3、包中新建文件:

4、定义一个构造:
既然要创建向量,肯定得要有构造,类似于java中的构造函数,如下:

呃,好奇怪的写法,而且__init__这么多下划线,对于习惯java的我来说看到python的这种写法还是挺奇怪的,其中self是代表当前Vector这个对象,完全不用声明类型,直接定义,好简洁,有机会一定要系统的学习一下python【看2021年有木有时间,到时立个flag】。
而对于创建向量肯定得要传一组数据,毕竟向量主要是用来表达一组数据的嘛,所以其构造里得增加一个参数由用户传进来,如下:
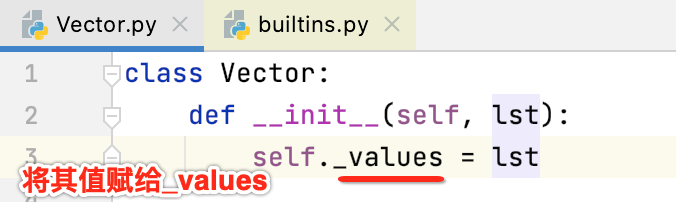
直接就可以给对象赋值了,不需要像java那样先在类中定义一个变量然后再接收。
其中对于这个__init__在python中称之为“魔法方法”,其实就可以简单理解成Python的内置系统函数。
5、__repr__定义:
对于java中要输出一个自定义类得定义它的toString()方法对吧,而在python中得定义__repr__,如下:
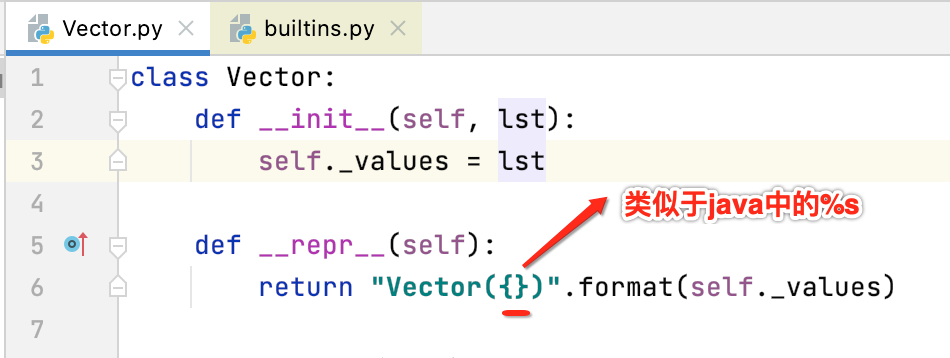
6、__str__定义:
这个也是管打印的,只不过它是供用户调用的,跟__repr__有点类似,关于这两者的区别之后会实际运行看一下效果就知道了,这里就输出向量本来的样子,也就是用()来将咱们的数组包裹起来,如下:

7、在终端运行看一下__repr__和__str__的区别:
对于这俩都是系统方法:
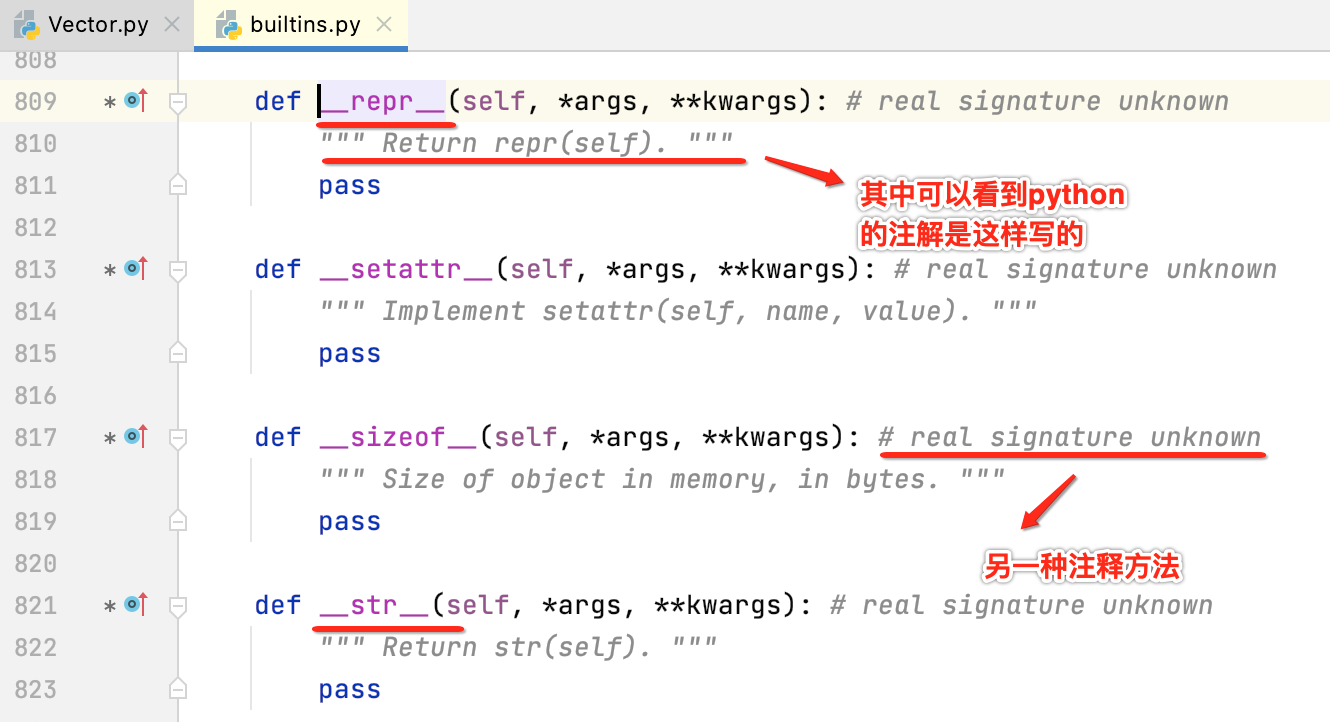
它们都是属于打印输出的,那具体有啥区别呢?下面在终端上使用python来调用一下咱们定义的这个Vector类:

8、创建测试文件:
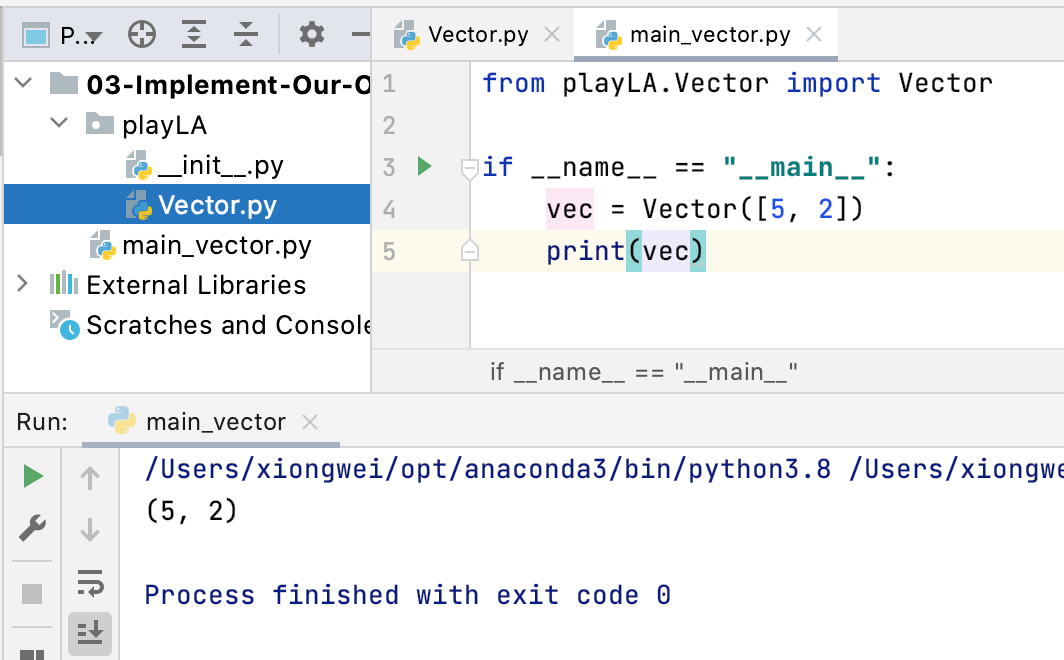
其中熟悉一下python的main()写法,跟java还是有很大的不同的。这样就正常的实现了一个向量。
9、__len__:返回向量有多少元素:
对于一个Vector向量可能需要知道它有多少个元素,此时可以定义一下:
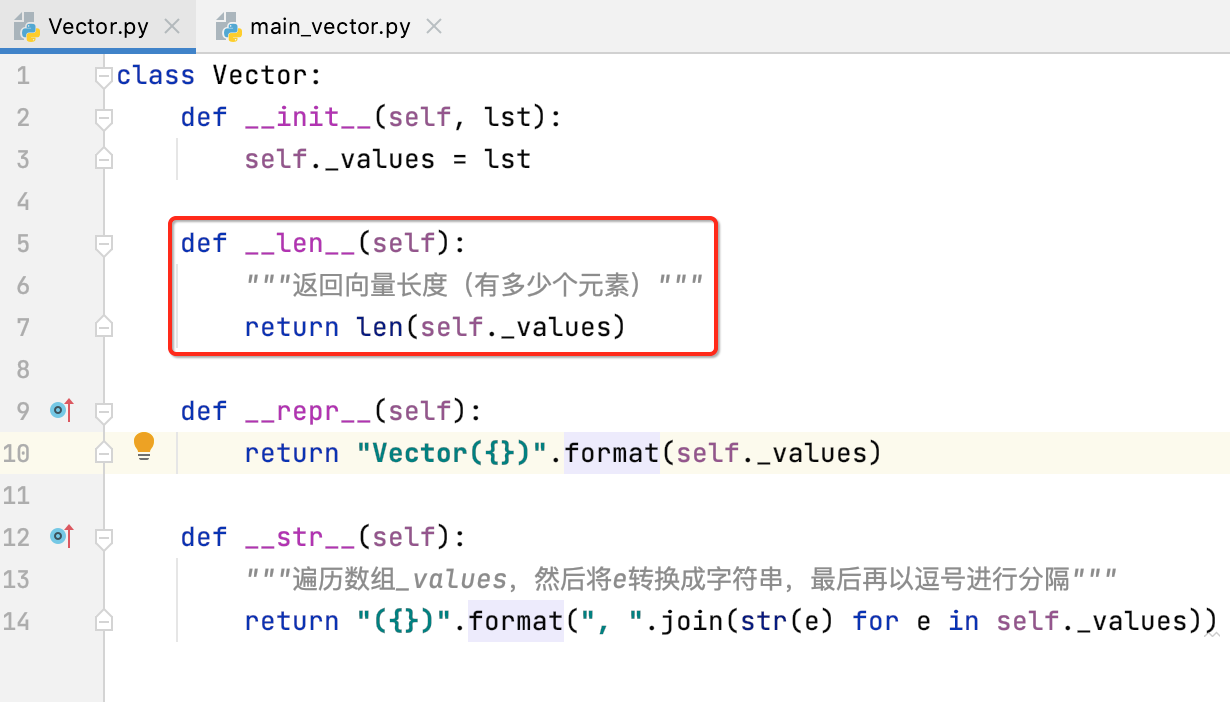
调用一下:
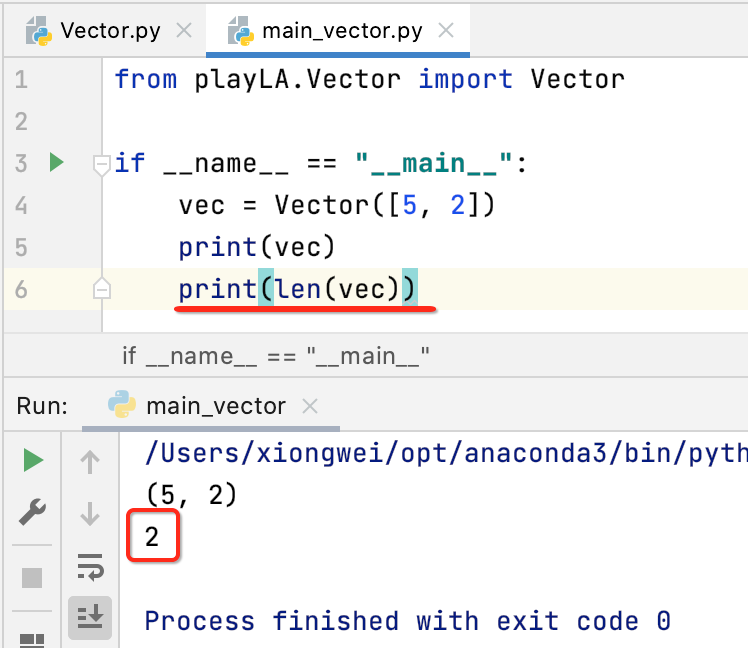
10、__getitem__:取出向量中的某个元素
如果想获取某个向量中的某个位置的元素咋搞呢?定义好相应的魔法函数既可:
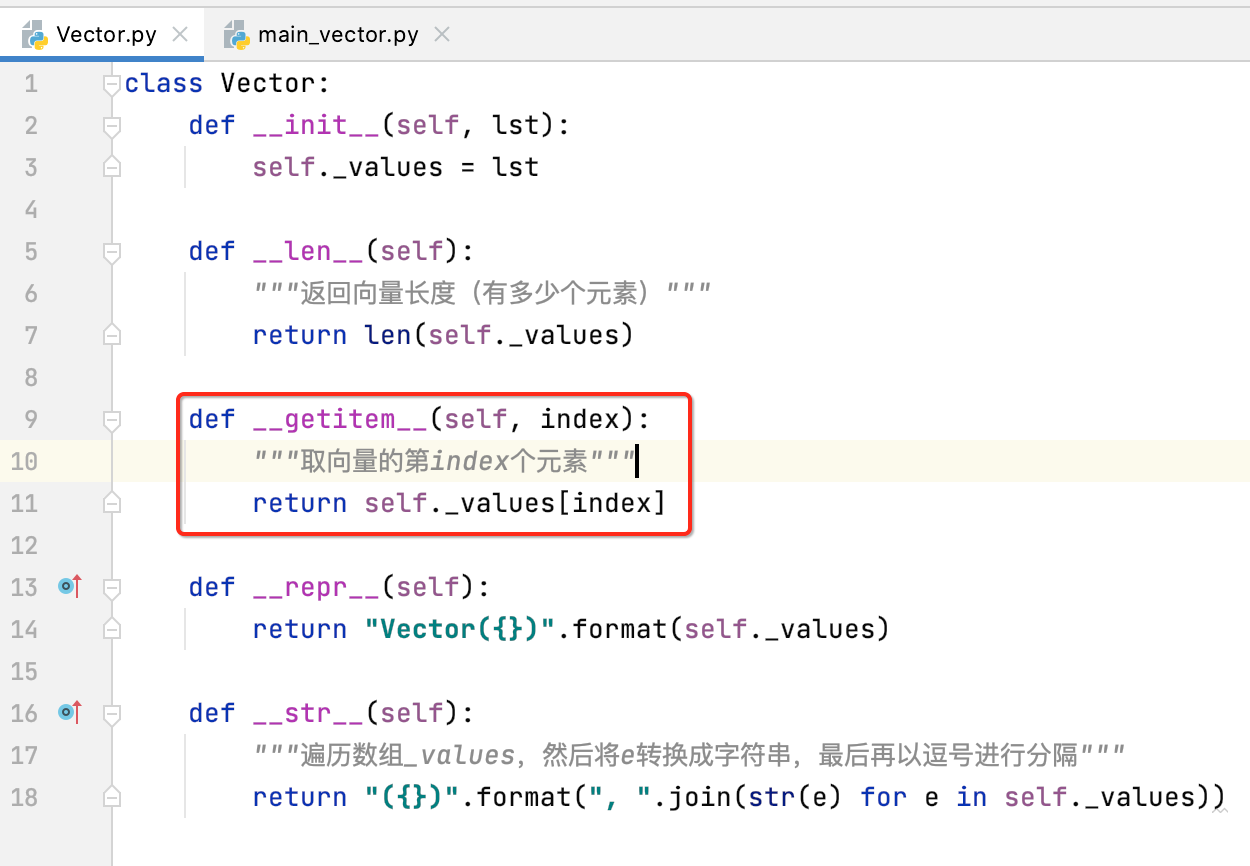
调用一下:
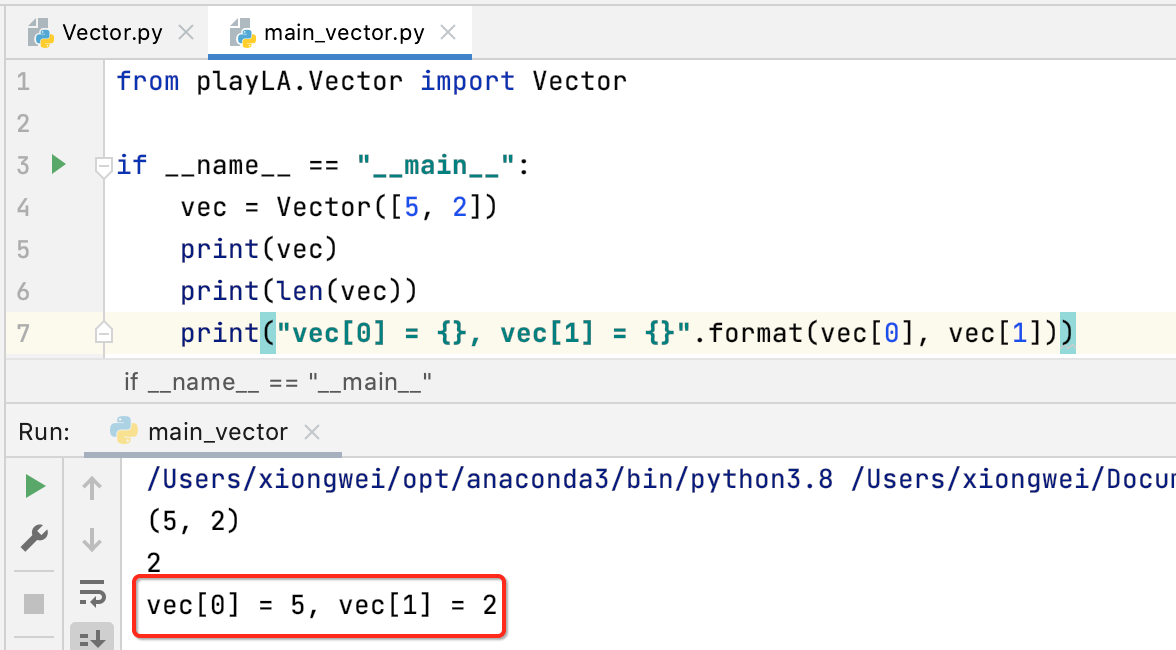
这样一个最最简单的Vector就已经实现好了。
向量的两个基本运算:
向量加法:
![]()
对于上面这个式子其结果是多少呢?其实在高中物理有这么一个原则:
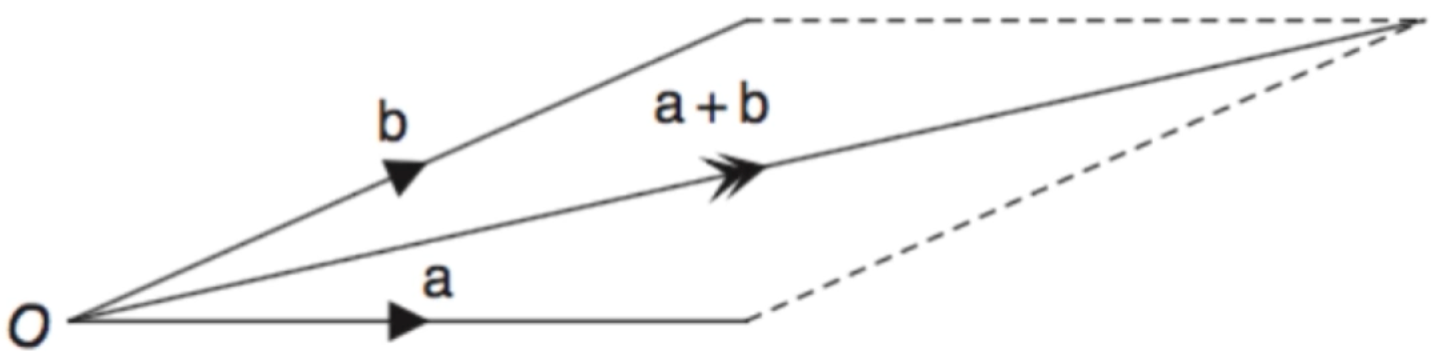
如图a、b两个向量,a+b的和是以a,b为边所对应平行四边行所对应的对角线的这个向量。根据这个原则很显然其结果为:
![]()
那向量的加法为什么要这么定义呢?下面将待添加的两个向量标在坐标轴上:
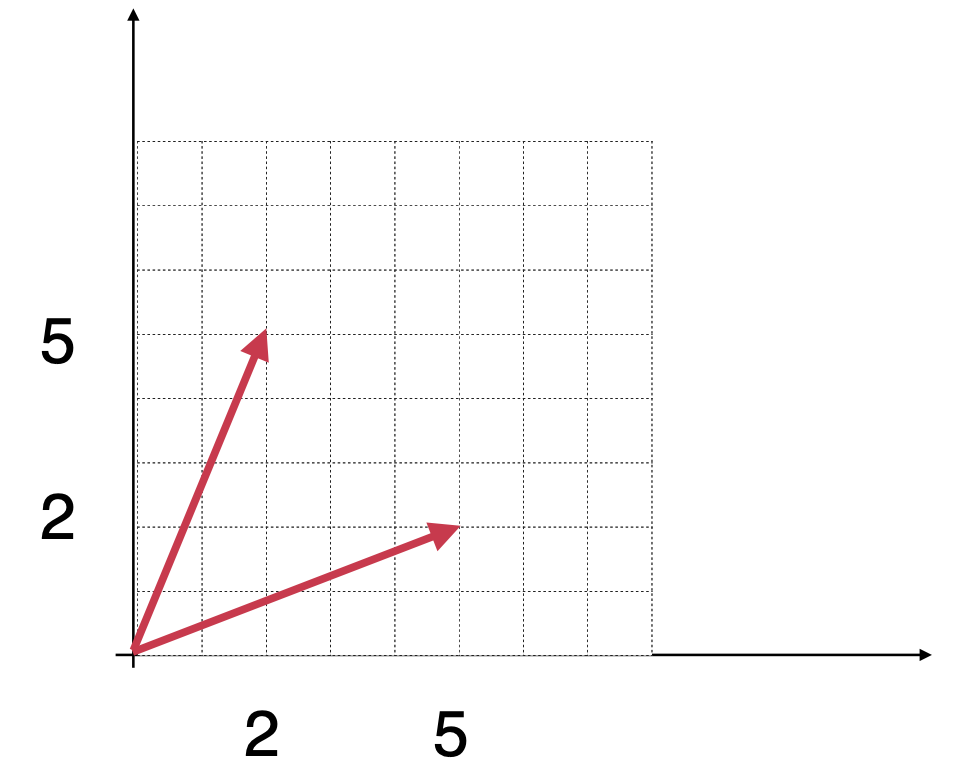
其实过程是这样:
a、从原点出发,先走到(5,2)这个位置;
b、再从(5,2)这个位置出发,再走(2,5)向量所对应的这么多个位移: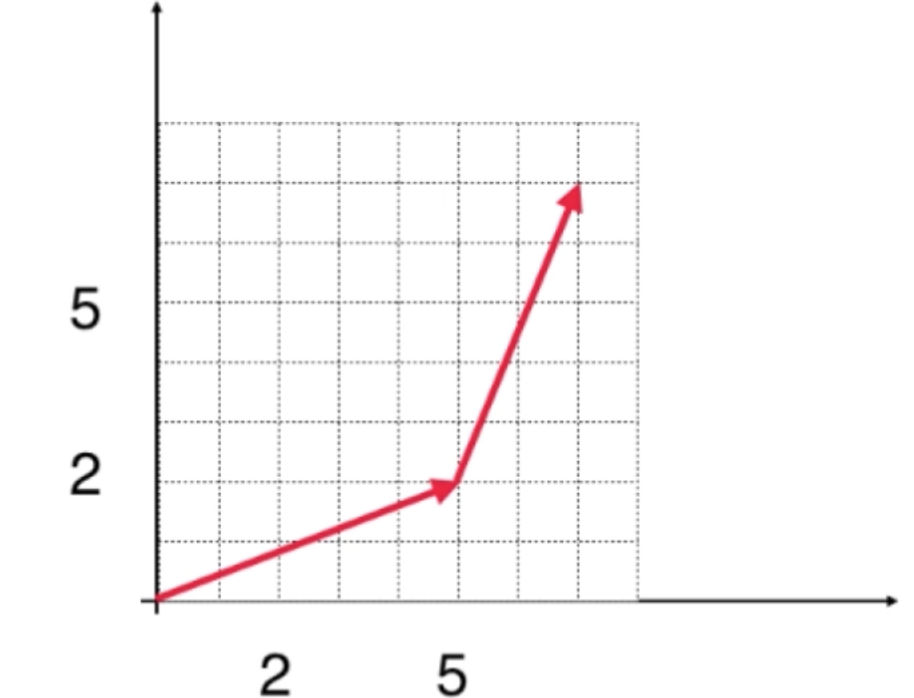
其最终的位置就是两个向量相加的结果,等于就是从(0,0)这个位置到(7,7)这个位置,也就是最终的向量为:

成了一个三角形的形状,那如果在三角形的另外一侧也补上跟待相加的向量平行的边的话:
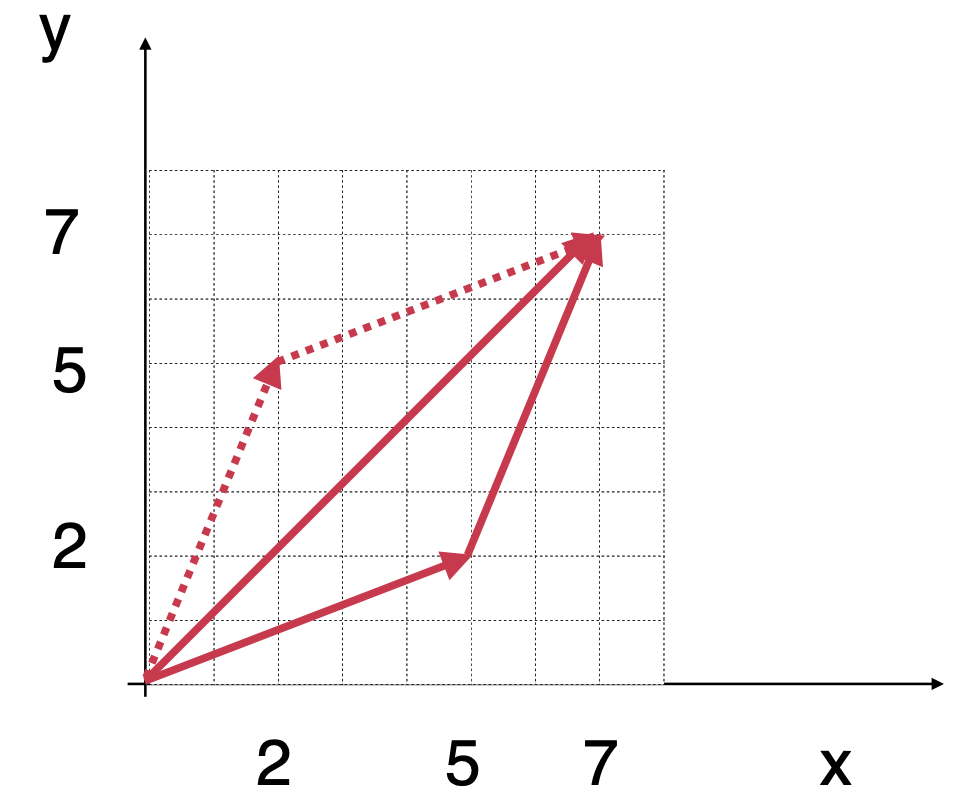
其结论是不是刚好就是上面物理上的这个规则?
那如果抽象一点来看的话,对于向量的加法可以是这样:
![]()
同样的,如果回到三维的世界的向量也同样满足,如下:
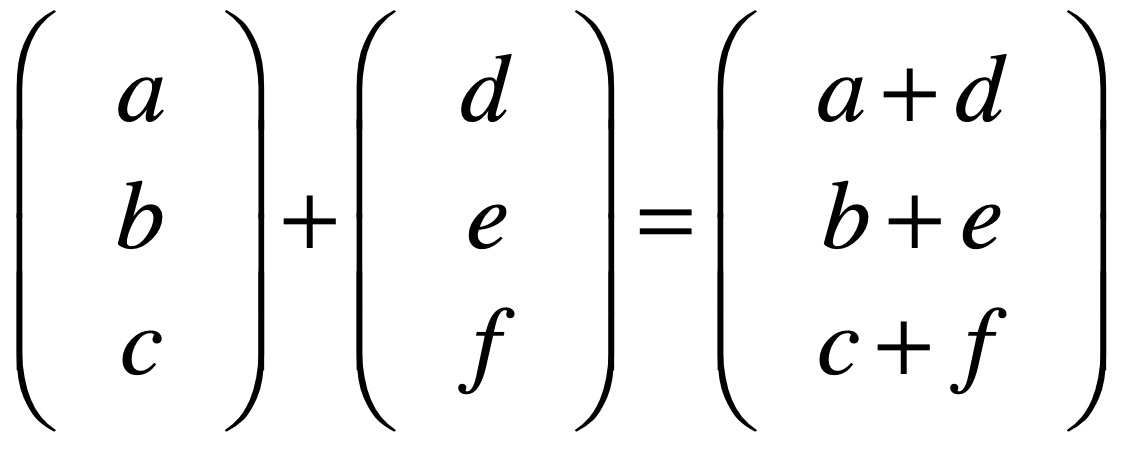
上升到n维也一样:
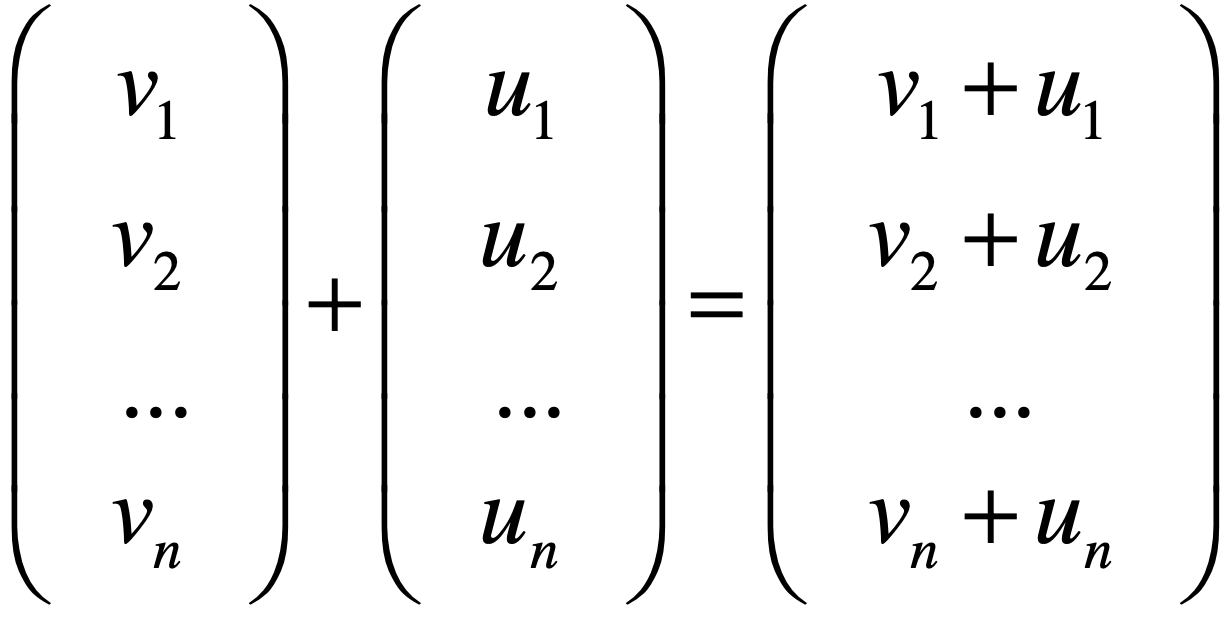
向量数量乘法:
上面这个小标题并非是“向量乘法”,而是在乘法前面加了一个“数量”,它是指的啥呢?其实它是长这样:
![]()
同样的回到坐标轴:
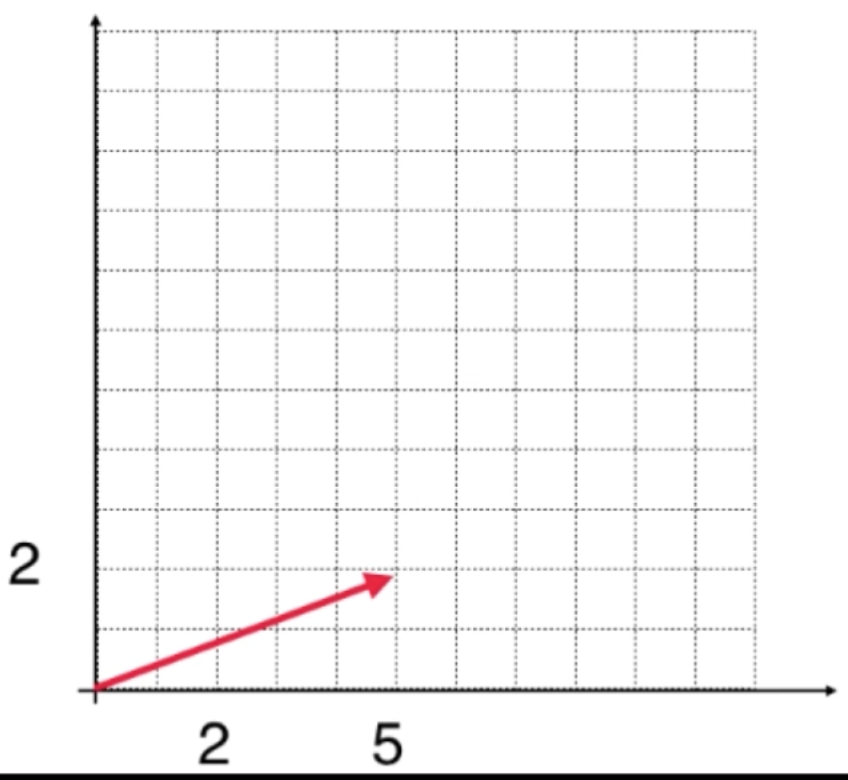
而根据我们数字的基本运算,对于算法的乘法其实就是多次的加法而已,回到咱们这个例子,其实它就是2个(5,2)向量进行相加,而根据上面向量相加的规则,等于会变成这样:
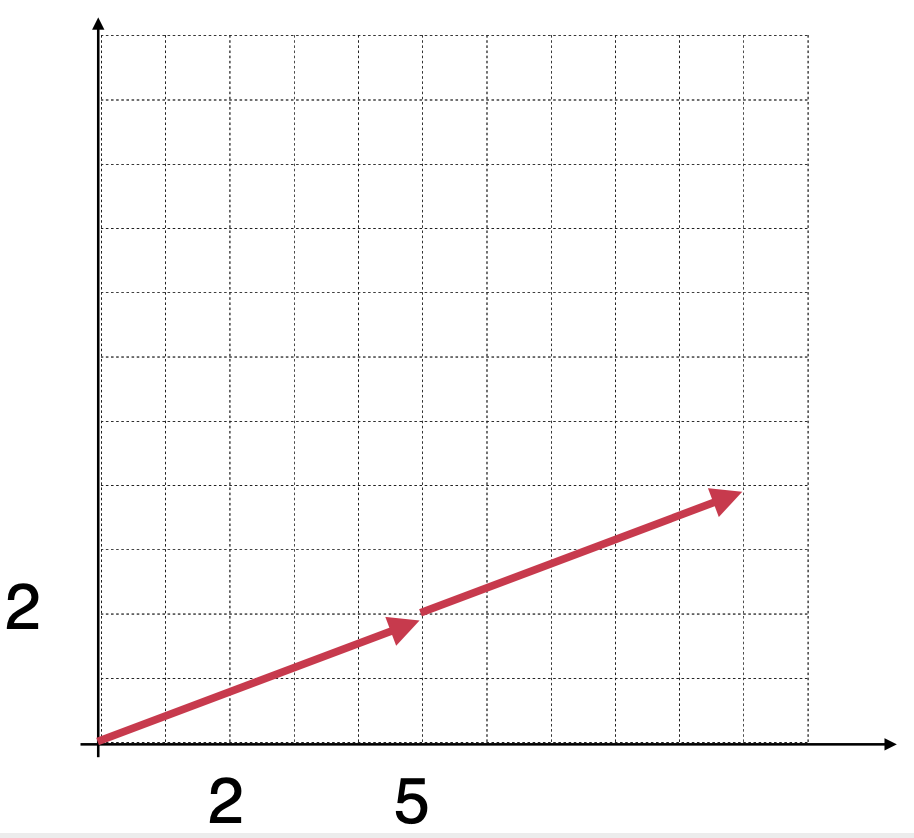
等于是从(5,2)这个位置再移动(5,2)个位置,同样的,如果抽象一点的话:
![]()
如果是n维:
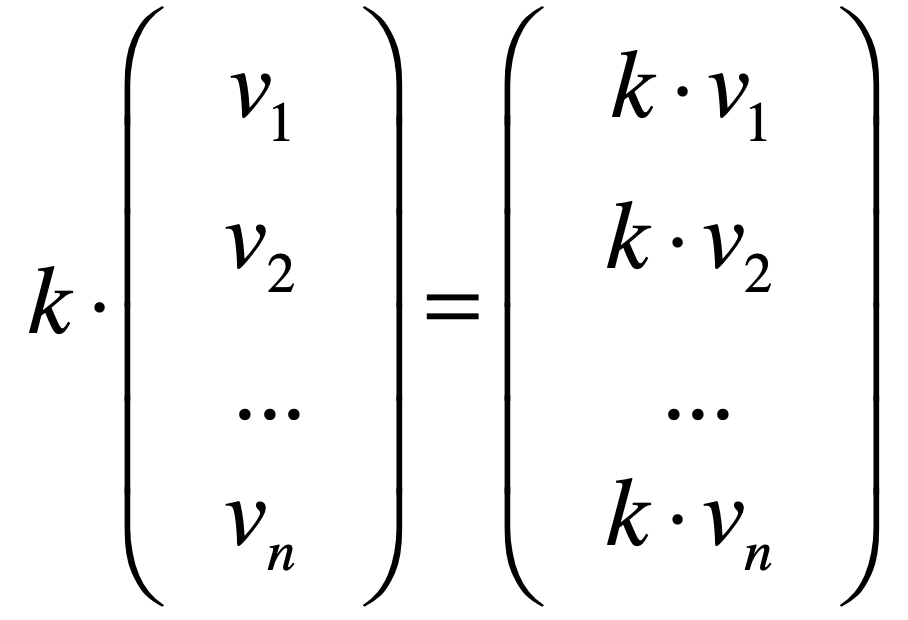
最后,对于这个向量的数量乘法跟向量的加法是不一样的,向量的加法是两个向量相加,而向量的数量乘法是标量*向量。
实现向量的基本运算:
接下来咱们则来编程实现一下上面所介绍向量的两个基本运算,回到python的世界中:
__add__:向量的加法
这里又定义一个相应的魔数方法:
而首先对两个向量的维度进行一个判断,只有相同的维度才能进行相加运算,所以这里先断言一下,那在python中是如何断言的呢?
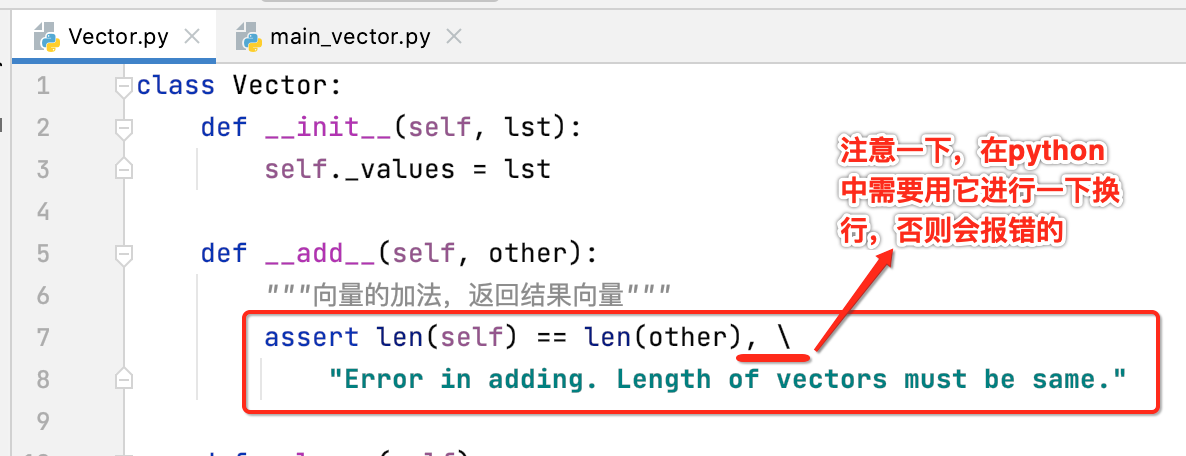
如果断言成功了,接下来则可以进行相加运算了,如下:

不过这里有一个待优化的点,目前IDE其实也给出了提醒了,把光标定位看一下啥提醒:
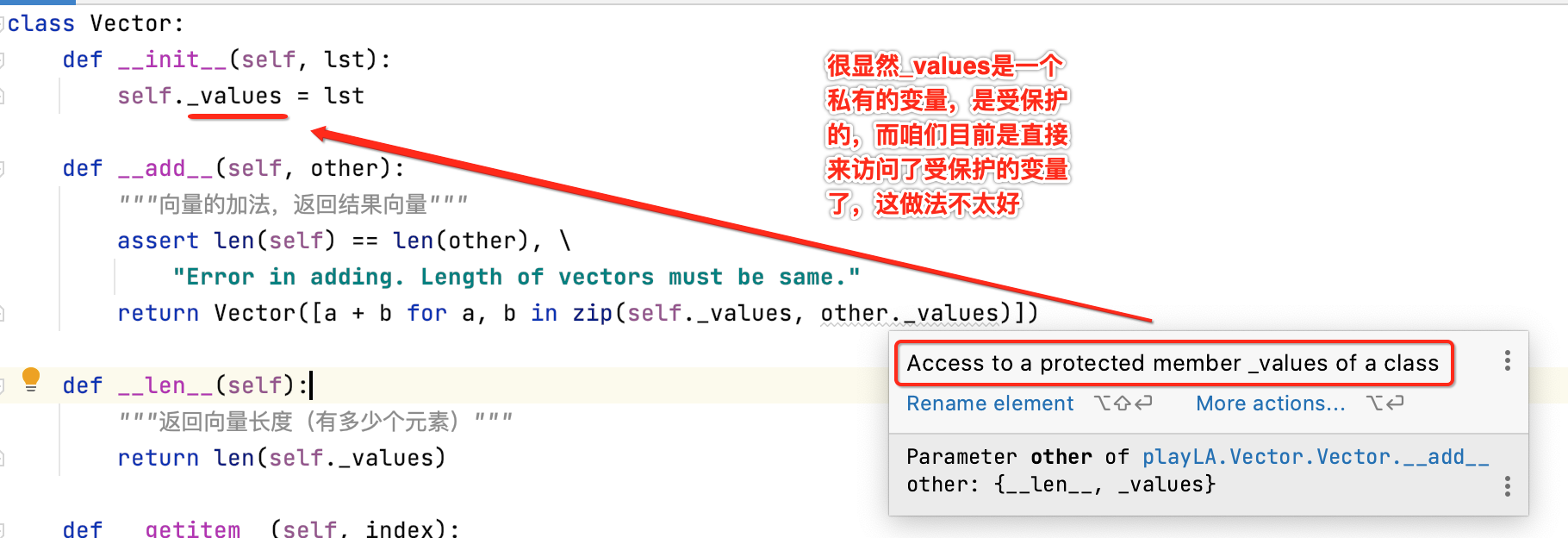
其实这里可以定义一个迭待器来解决,如何定义迭待器呢?如下:
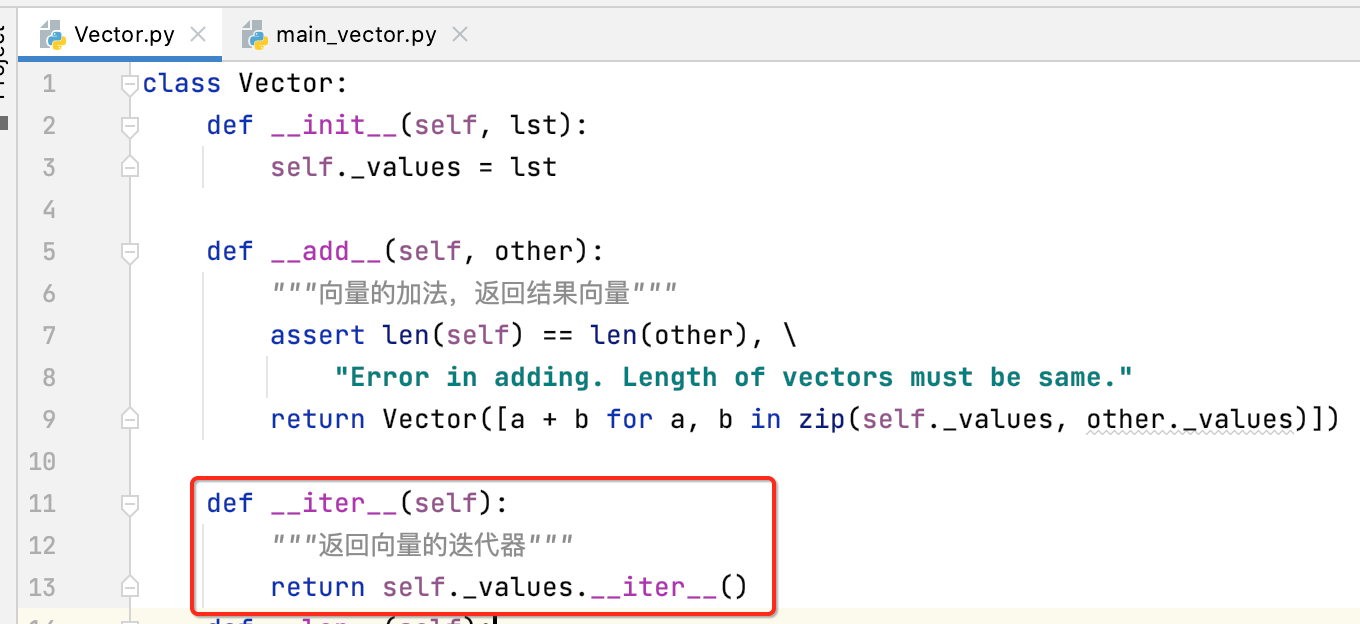
此时对于__add__的实现就可以不去直接访问受保护的_values变量啦,而是直接使用向量既可,更改如下:
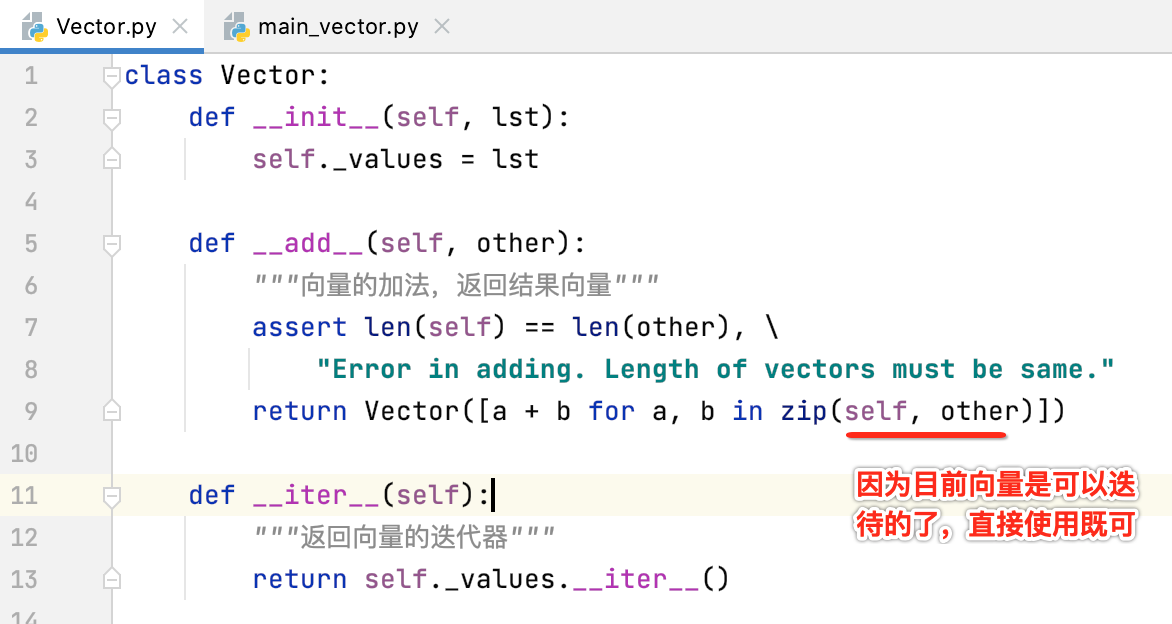
这些都是Python语法的知识,还是那句话,不了解木关系,对它有个感性的认识能敲出来既可,毕竟重点是学习线性代数,而不是研究Python语法,这一点需要了解。另外关于目前的实现还是有一些小缺陷待改善,啥缺陷呢?
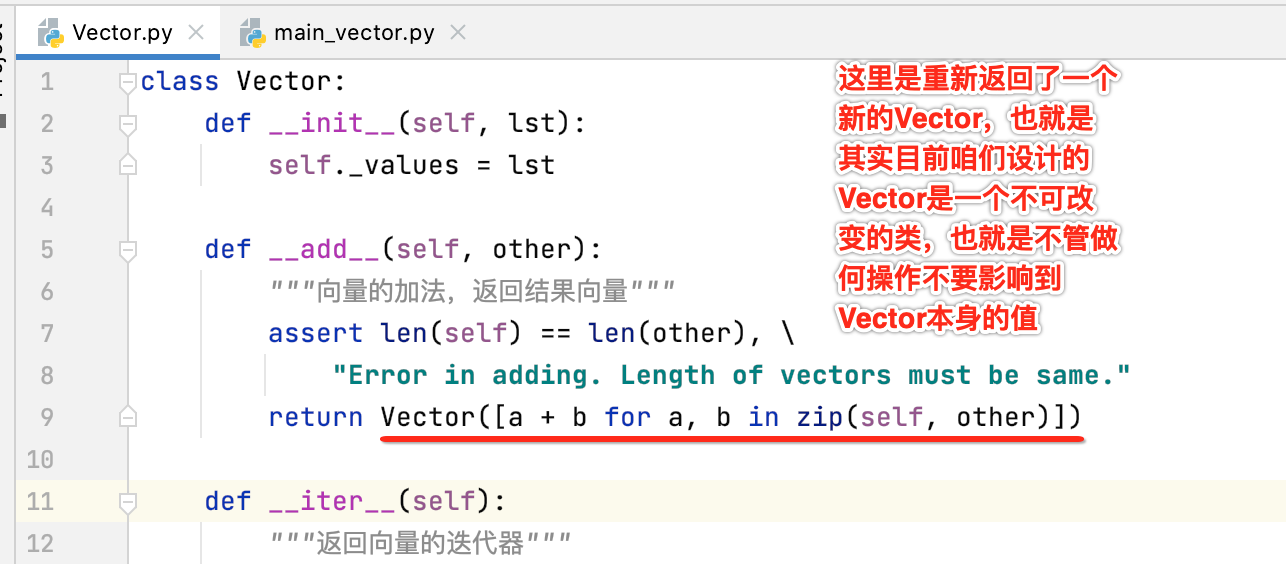
但是!!!这里矛盾点出来了:
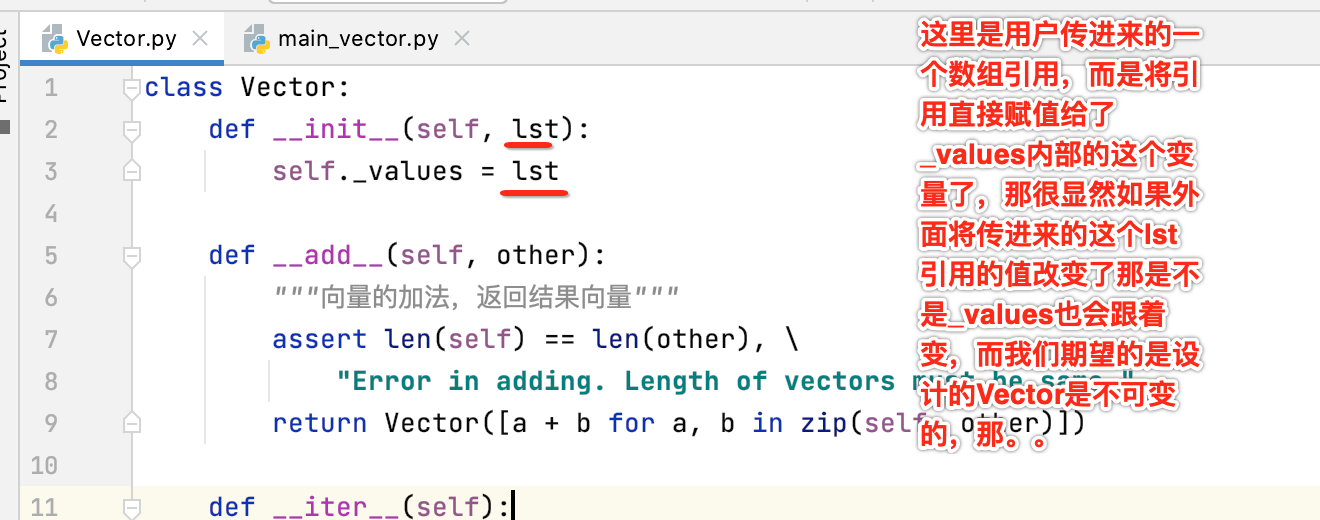
所以解决办法很简单,copy一下之后再来赋值给_values,如下:
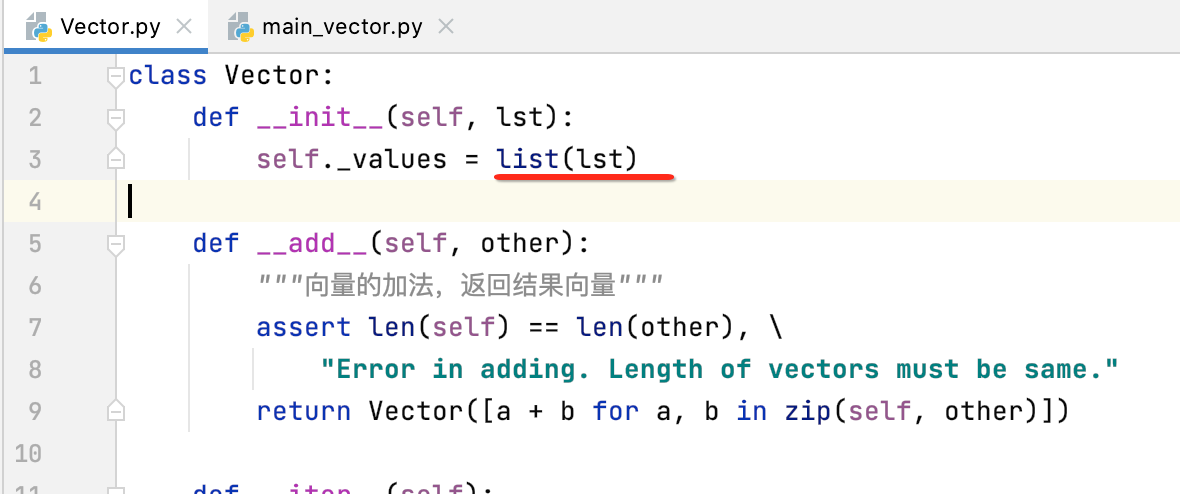
下面测试一下咱们的加法:

__sub__:向量的减法
既然实现了向量的加法,对于它的减法操作那就轻而易举了,因为减法操作其实也是一个加法,如下:
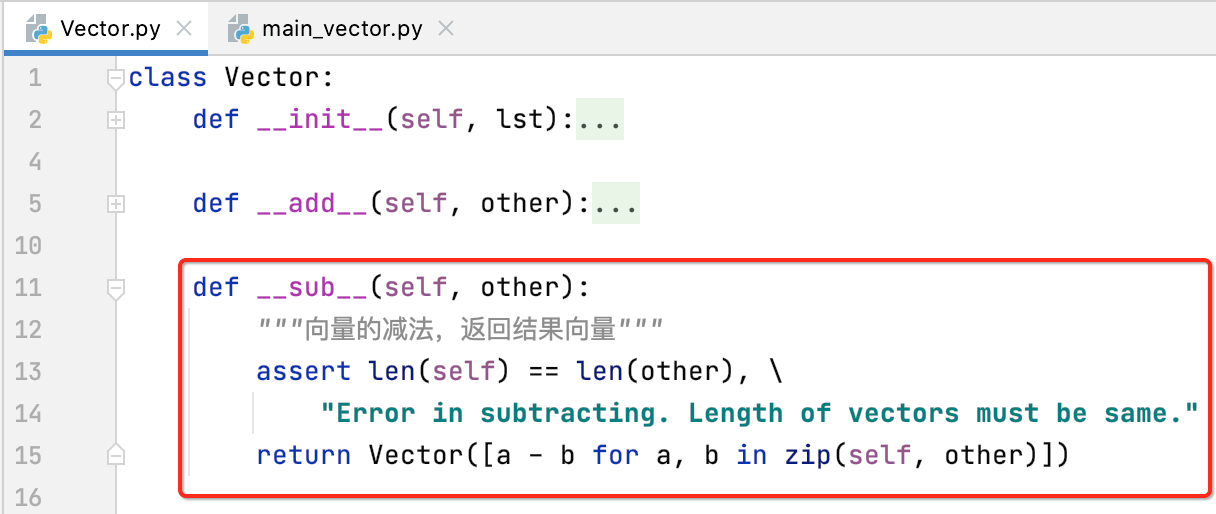
运行一下:
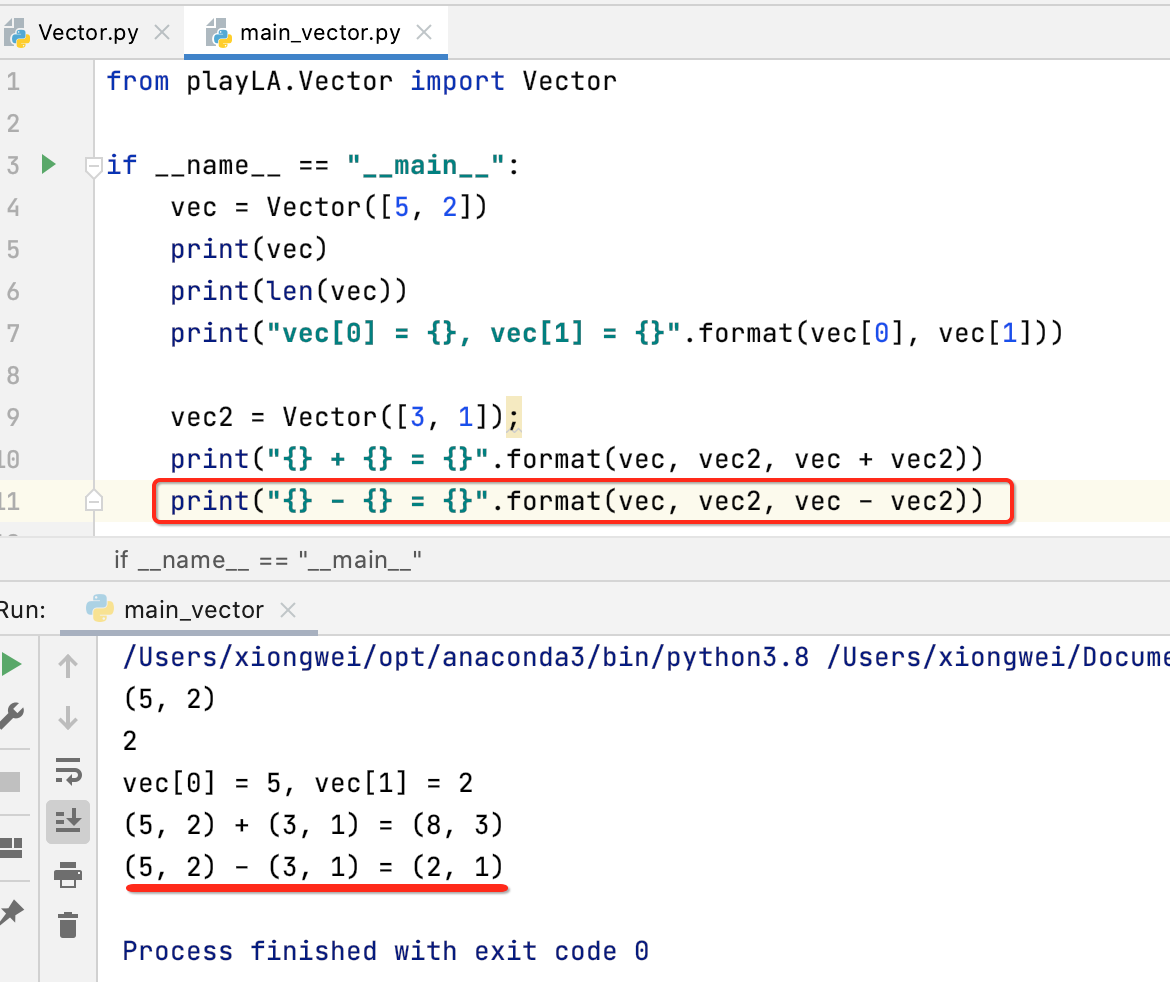
__mul__:向量的数量乘法
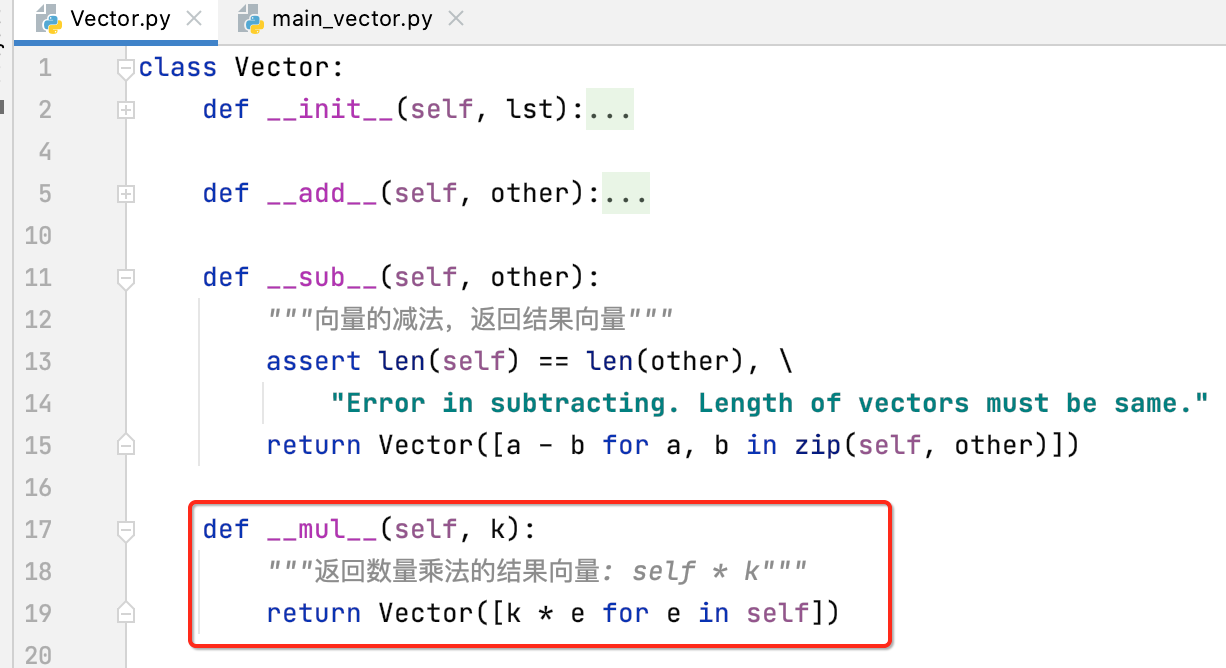
运行看一下:
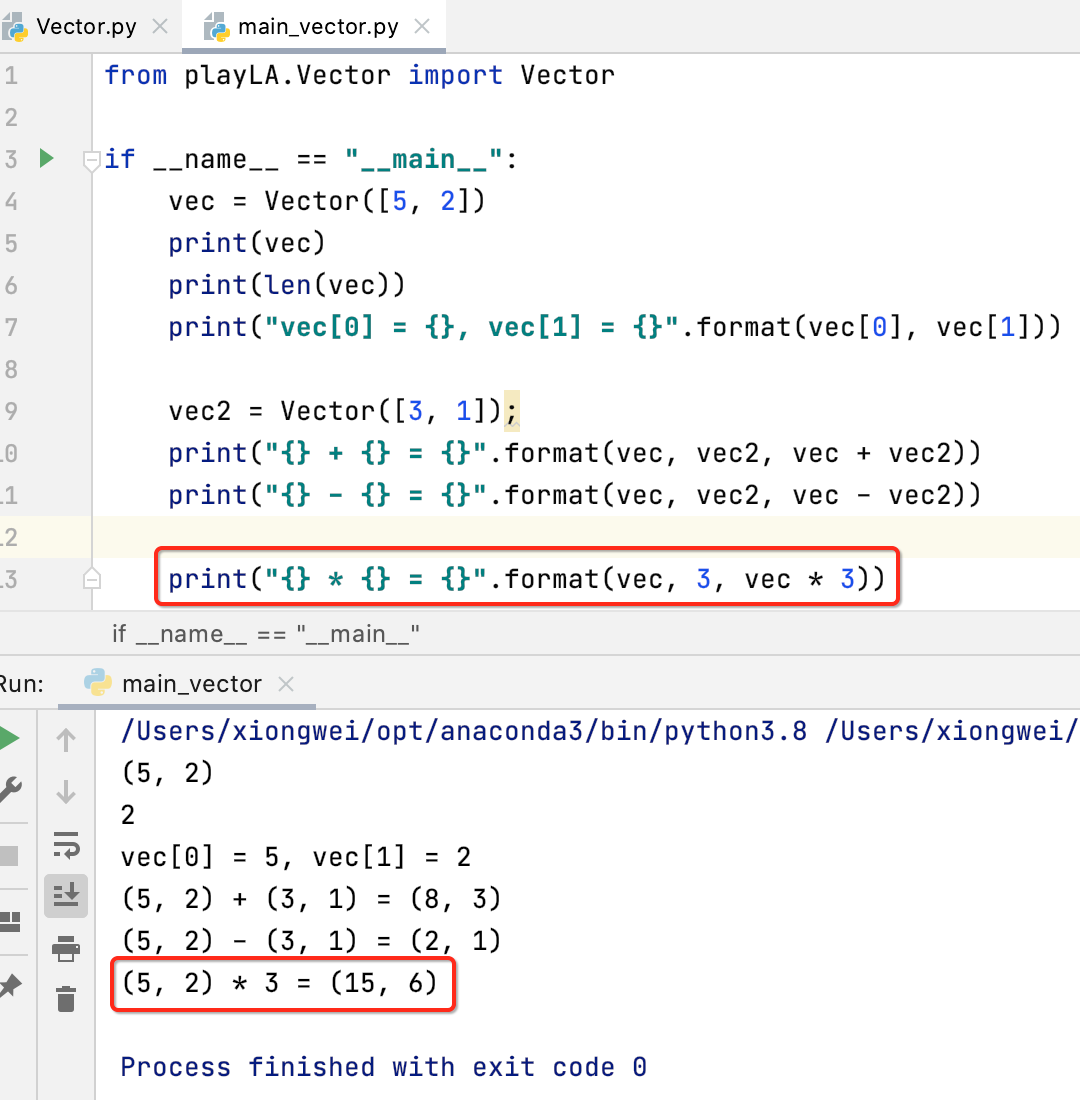
但是!!!这里有一个坑,再来修改一下调用:

原因是由于咱们只定义了一个向量乘一个数的魔法函数:

解决办法当然是定义另一个对应的函数喽,不过这里是这样写的:
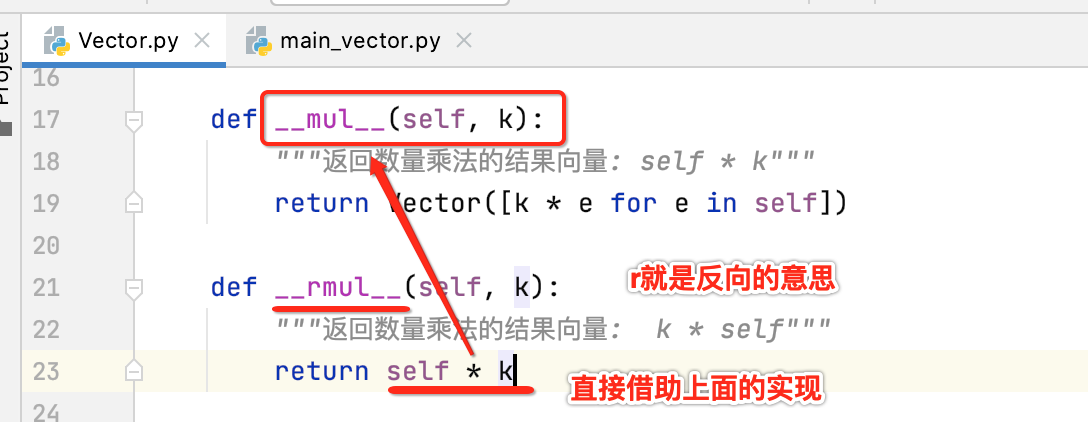
再来运行一下:

__pos__、__nag__:向量取正、向量取负
利用向量的数量乘法,咱们可以再封装两个辅助方法,就是对向量取正负,实现如下:
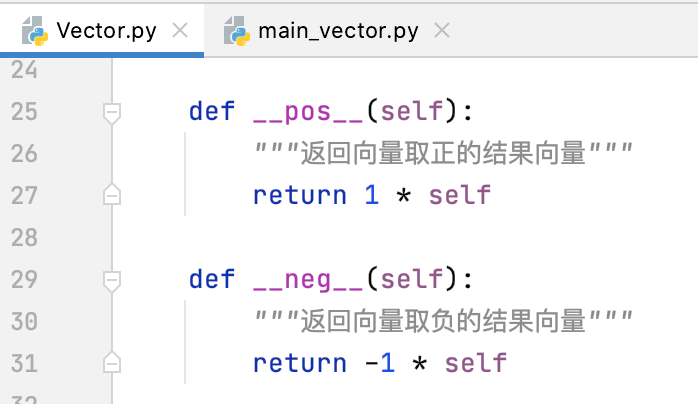
调用一下:
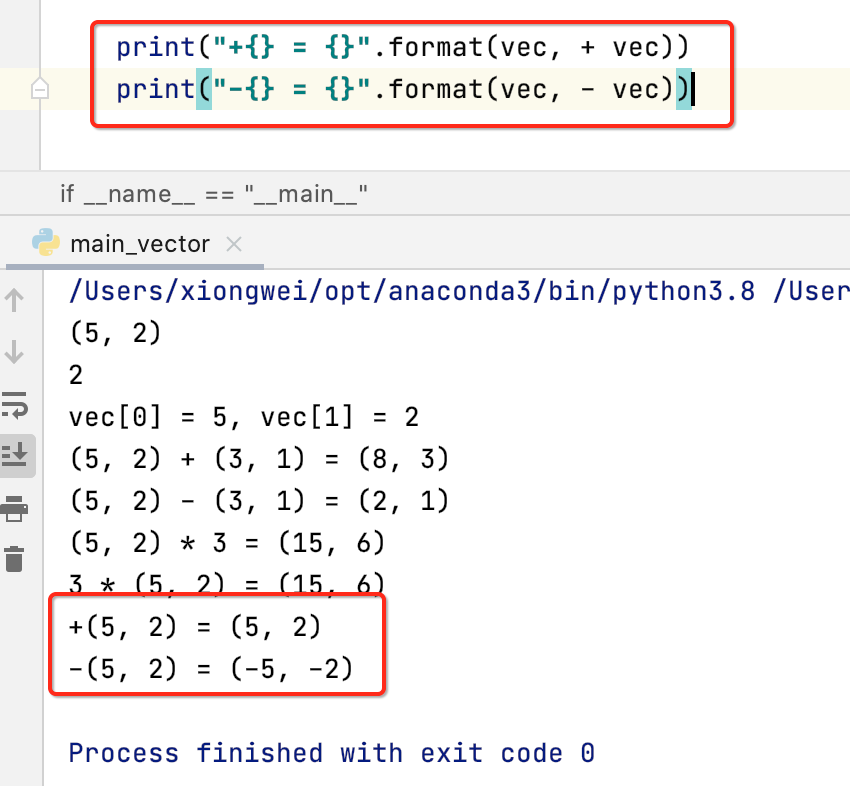
向量基本运算的性质与数学大厦的建立:
这里其实是一个纯思想层面的东东,回忆我们小学时学习的数的运算 我们也要先有数的运算的相关性质,之后才敢进行更加复杂的运算 ⽐如:加法交换律,乘法交换律,加法结合律,乘法结合律等等。对于向量运算,我们也要这么做! 毕竟向量是定义的全新的东东,并不能保证它能满足之前在数这个世界中所定义的所有的性质。
那向量的基本运算性质都有哪些呢?
1、加法的交换律:![]()
2、加法的结合律:
![]()
3、数量乘的分配律:
![]()
还有另一个形式:
![]()
4、数量乘的结合律:
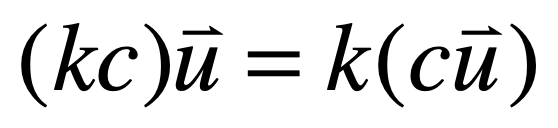
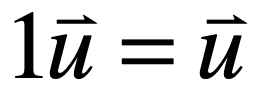
数学证明:
对于上面这些性质说实话太简单了,感觉没必要提出来,但是!!!这里主要是要来体现数学的所有结论都是可以证明出来的,而不是拍大脑说这个公式就是这样之类的,所以为了突出这么一个重要的思想,下面以数量乘的分配律为例进行一个严谨的证明:
![]()
要论证则需要使用咱们现在已经拥有的定论来进行,而目前关于向量的算法已知的定论只有加法和数量乘法,下面就以这俩来进行上面这个式子的论证,先来将等式左边的进行一下扩展:
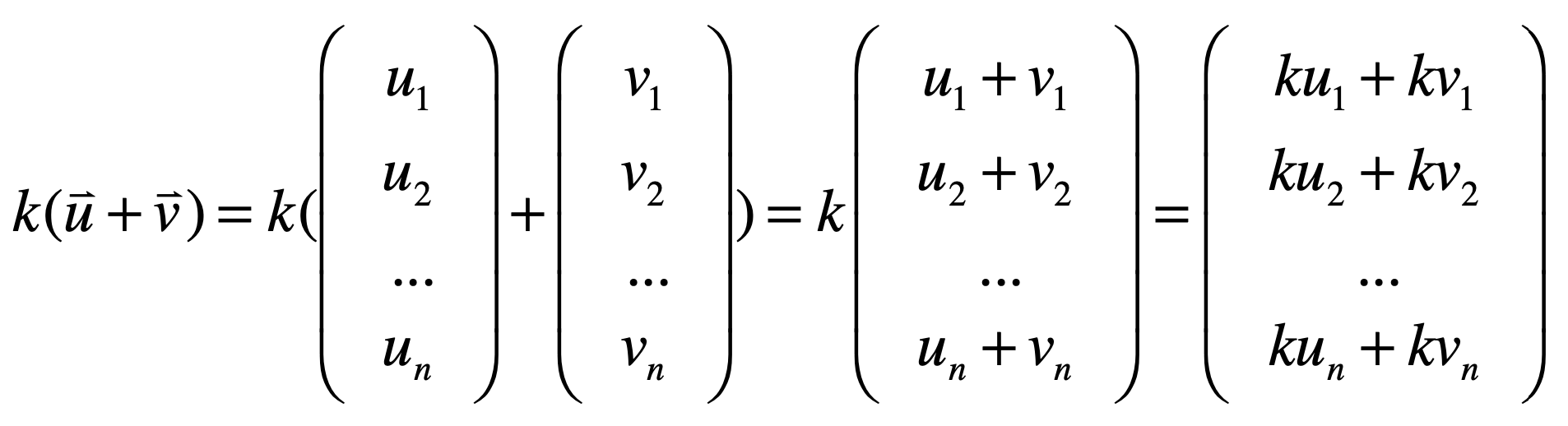
上面这个推导是很顺其自然的对吧,分别是利用向量的加法和向量的数量乘法公式推演而来,接下来重点是来看看等式右边的扩展之后是否跟等式左边扩展的一模一样,如果一模一样那当然就可以成功的论证的向量的数量乘的分配律是对的,如下:

然后看一下扩展的结果:
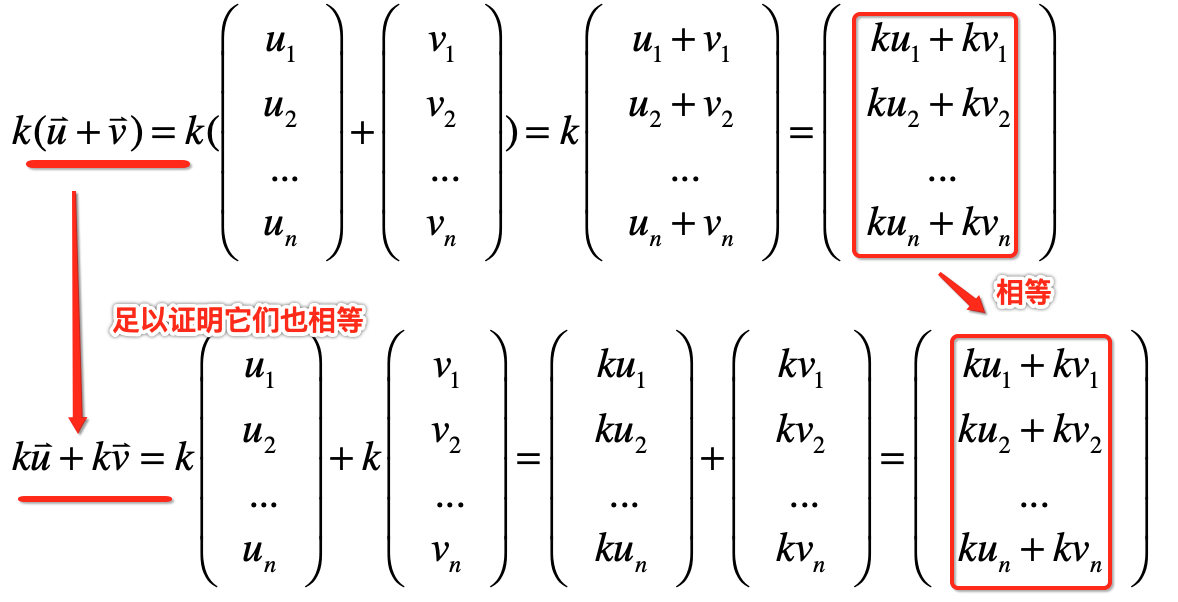
所以可以体现出其实也就是由这些严谨的定论也就是构成了数学大厦的一个体系,既使非常复杂的数学公式都是由若干个小的论证给证明出来的,知道这点就好。
零向量:
我们知道对于一个数它也有一个0,同样的对于向量而言也存在零向量,但是这里并不直接给“什么是零向量”,而是还是像上面所说的我们从推导出一个“性质”出发,推导如下:
![]()
其实上面这个性质也是根据之前我们所熟知的数的性质所想象的,毕竟在数字的世界中任何数+0都等于它本身对吧?如果说能论证上面的这个等于成立,那是不是零向量确实也就存在?所以下面开启证明之路:
假设:
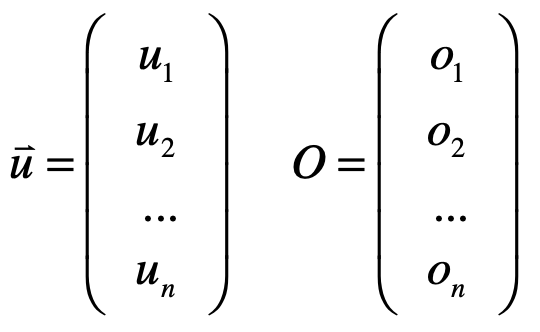
而根据向量的加法运算可以得知:
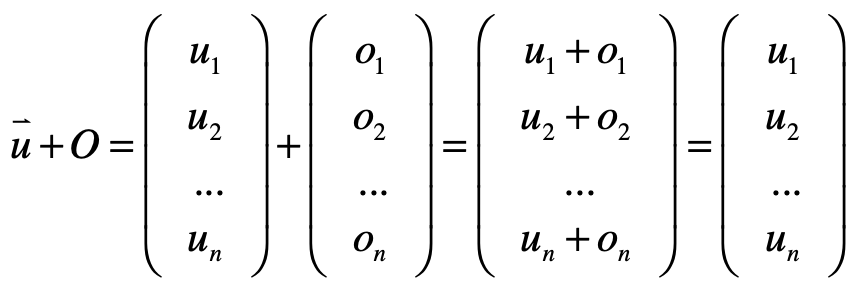
此时就需要满足这样的一个方程组:
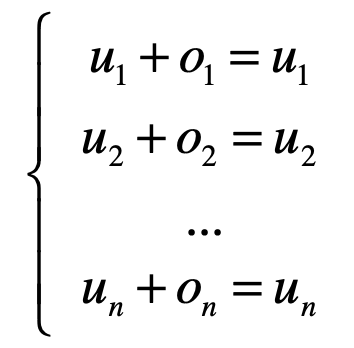
而解上面方程组的中每个方程式来说非常之简单,拿第一个方程式来说,等式左右两边可以都减去u1,同样的对于其它的方程式也一样,最后则就变成了:
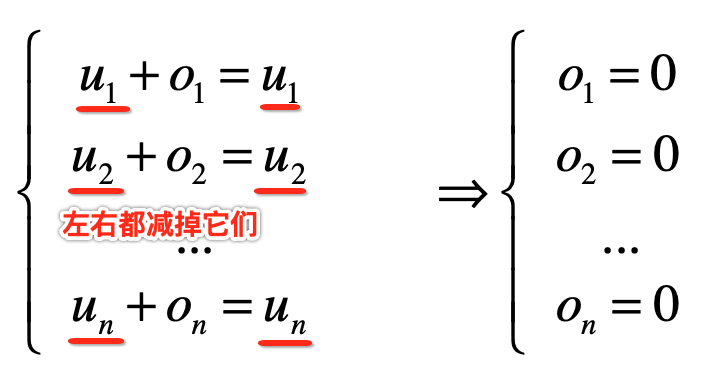
那是不是就可以论证:
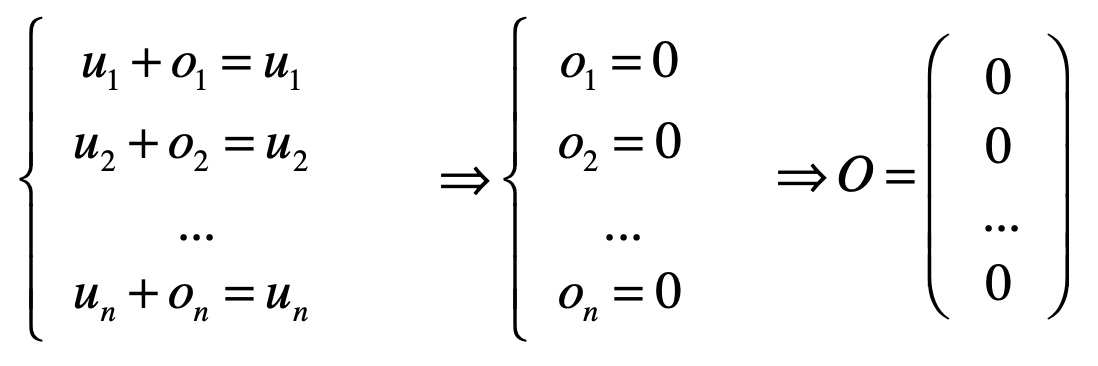
这个O向量就是各个维度都为0的这样一个向量呢?所以此时就可以称这样的向量就为零向量,注意:

正常向量的表示法不是这样的么?

这是因为零向量就是坐标的原点,不能代表一个方向,想想是不是?
和数一样,既然已经存在零向量这个概念了,接下来就可以定义负这个概念了,也就存在这样一个性质了:

对于上述这个性质的论证可以用一个反证法:
![]()
那下面可以这样来推理了:
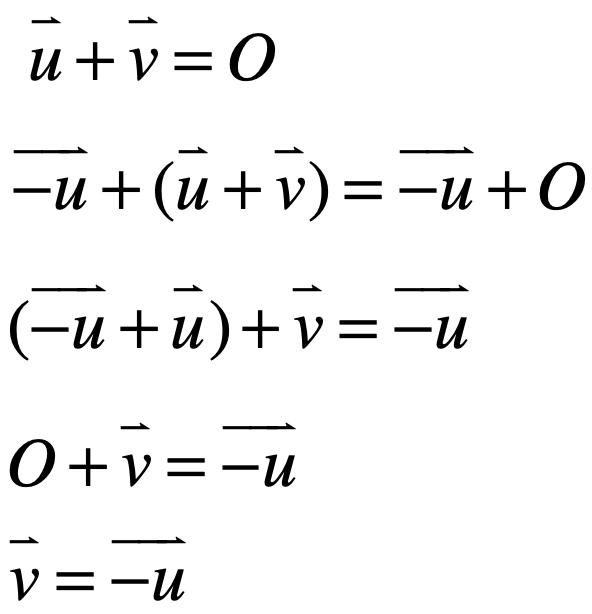
而论证的结果刚好跟它矛盾了:

那也就证明:
![]()
是不成立的对吧?
最后还可以推导出这么一个性质:

【温馨提示】:由于是刚刚进入线性代数的世界,所以这里涉及到一些论证的过程,但是之后学习不会这么细了,毕竟还有很多其它新的概念需要了解,这里重点是从程序员的角度来学习线性代数,而非是以高等教育考试的角度来学习,这一点是需要明确的。
实现零向量:
接下来则来编程实现一下,这里就不是定义魔法函数了,而是定义一个类方法,如下:
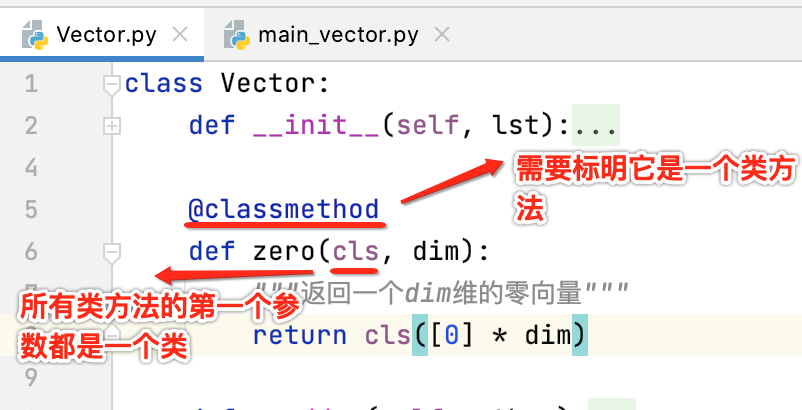
既然是类方法,其实就类似于java中的static方法,直接通过类名的方式来调用既可,如下:
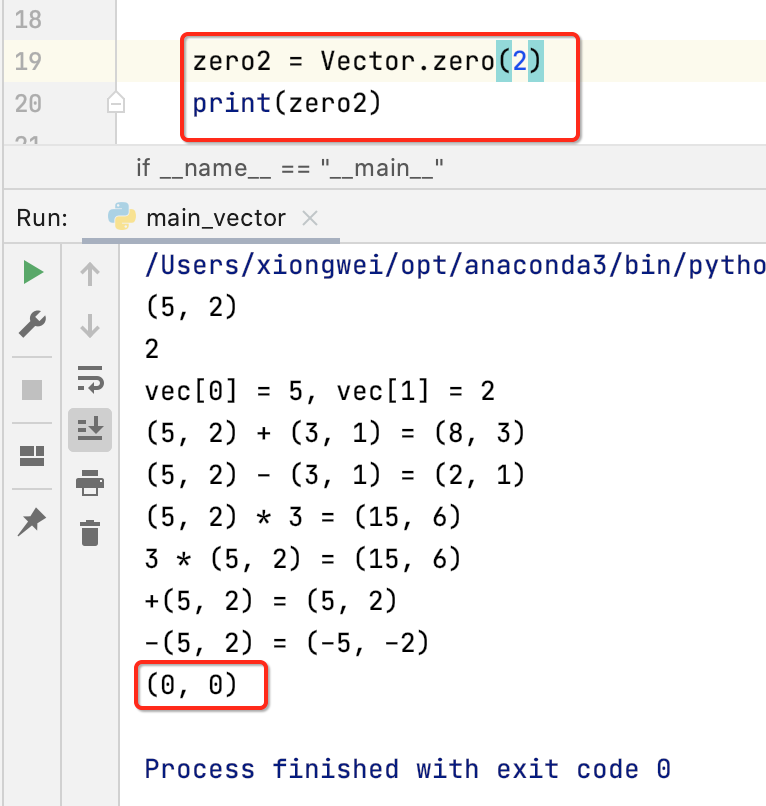
那来做一次加法试一下:
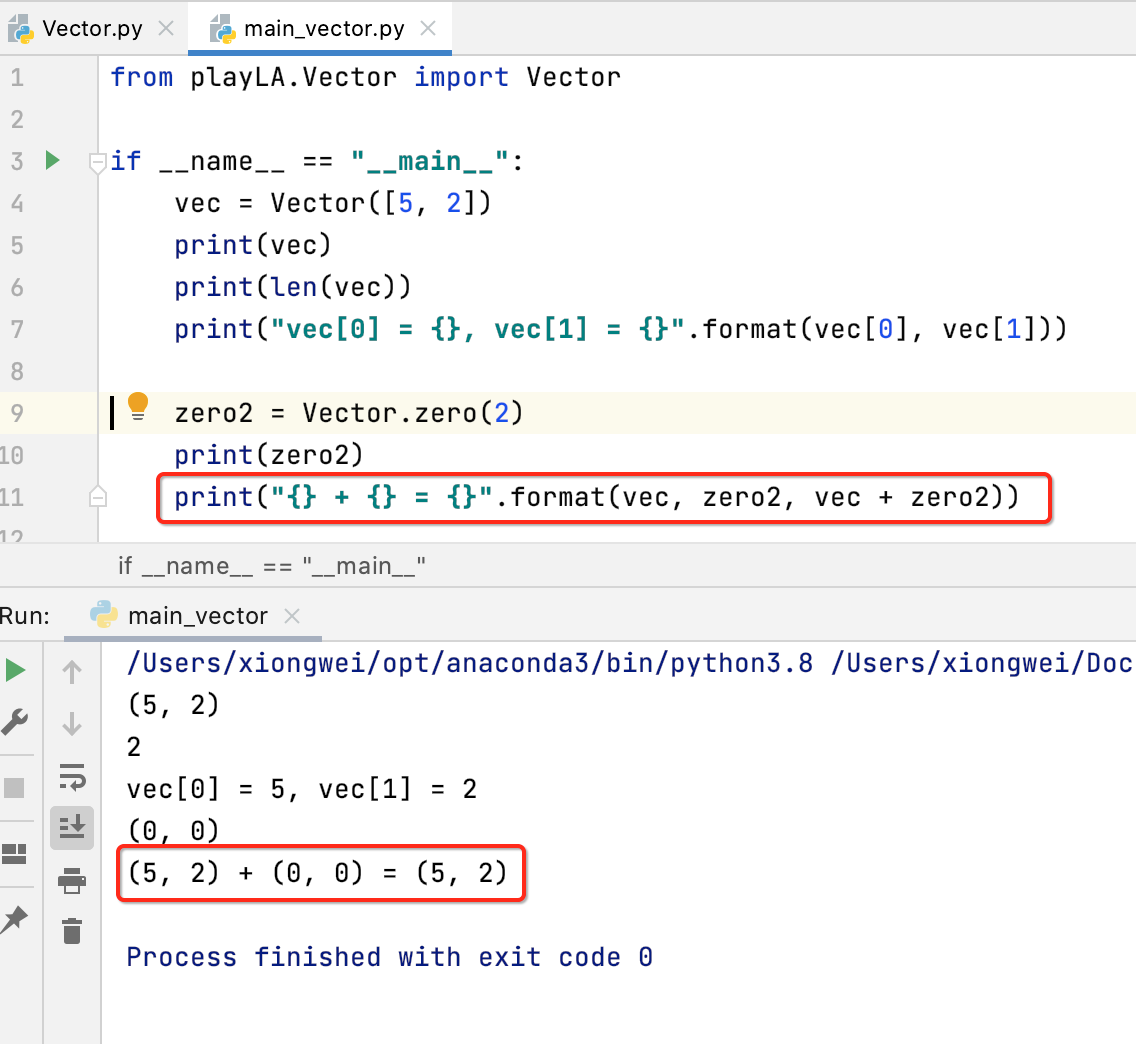
总结:
这是关于线性代数学习的首篇,很枯燥,但是呢如果深入其中也是蛮有意思的一个基本功,重点是自己要梳理练一下,才能将枯燥的内容变得生动形象,以此篇来激励自己,一定要完整的学完它,要半途而废的话自己就是xx。。另外对于这门课涉及到N多Python的一些语法的东东,莫要太过纠结语法是什么意思,直接干就完了,于我而言我也还没接触过Python,但是并不阻碍对这么课程的学习之路,不懂装懂呗,然后随着之后时间的推移再将这些“装懂”的给“搞懂”就可以了~~