---恢复内容开始---
树的逻辑结构表示有树形结构文氏图结构和凹入表示法和括号表示法
基本术语
结点的度:最大度
树的度:结点总度:
分支结点:有后继结点的结点
叶子结点:没有后继结点的结点
孩子结点:一个结点的后继结点
双亲结点:一个结点的前驱结点
子孙结点:一个结点的子树当中除去本身的结点
祖先结点:从树根结点到达某个结点经过的所有结点,不包括本身
兄弟结点:
结点层次:根节点为第一层
树的高:最大层次
森林:有零个或者多个不交错的树
性质:
树中的结点数=树的度+1
度为m的元素 第i层最多有m^(i-1)个结点 (满树的时候根节点有m度 第i-1有m^(i-1)度该度也就是第i层的结点数)
m次树也就是最大度为m 但n个结点构造树 但为m次树或者接近满m次树的时候 树的高度层数最小
/* 高度为h的m次树最多有多少个结点? m+m^2+m^3+...+m^(h-1)总度数 再加上跟结点1 就是m的h-1次阶层 也就是m^0+m^1+m^2+m^3+...+m^(h-1) */
因为树的结构为非线性结构因此树的运算较以前讨论的线性结构复杂
主要运算有:
寻找满足某种特定关系的结点 如寻找当前结点的双亲结点等等
插入或者删除某个结点 如在当前的结点上插入一个新的结点或者删除当前结点的第i个孩子结点等
遍历树中的每个结点 主要有先根遍历、后根遍历和层次遍历三种 前两者需要用到递归知识
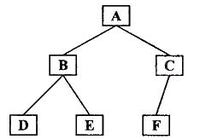
存储一棵树不仅仅要存储树中的结点的值还要存储结点与结点之间的关系
双亲存储结构(使用数组存储)
每个结点包含当前结点值还有双亲结点在该数组当中的下标,但parent下标为-1时该节点为树的根结点
特点:寻找双亲结点容易找孩子结点难
孩子链存储结构
使用链表该链表的每个结点用于保存当前值以及指针指向所有孩子结点 由于孩子个数是未知的因此相当耗内存
特点:寻找孩子简单 但找双亲难
兄弟链存储结构:
每个结点有一个data保存值 一个left 指向第一个孩子结点 right指针指向兄弟结点
特点:跟孩子链存储结构相似,不过是二叉树因此节省内存空间
二叉树与树都属于树形结构但不能将二叉树定义为树的特殊情况
二叉树新性质
编号

满二叉树
完全二叉树:除最后一层,其余都是满的,任何一个结点的右子树高度为h则左子树的高度为h或者h+1
在有n个结点的二叉树中:
但第i个结点满足2*i<=n则i为分支结点
分支结点i的左孩子为2*i
右孩子为2*i+1
其双亲结点i/2向下取整
二叉树的存储结构:
数组存储
数组下表表示为结点的编号 空结点存储#字符
链式存储
每个结点的有两个指针一个值
一个指针指向左孩子 一个指针指向右孩子
有时候为了方便查找双亲结点可以添加一个parent指针用于指向双亲结点
在树型数据结构当中就需要时会用到递归
递归模型有递归体和递归出口
#include<iostream>
using namespace std;
/*递归*/
int sum(int data){
if(data==1||data==2){
return 1;
}else{
return sum(data-1)+sum(data-2);
}
}
int main(){
cout<<sum(10);
return 0;
}
递归出口
if(data==1||data==2){
return 1;
}
递归体
sum(data-1)+sum(data-2)
这种自上而下将问题分解、求解、再自下而上引用、合并、求出最后解答的过程称为递归求解过程
链表当中 求解最大值我可以使用一个数组模拟如下
int getMax(int arr[],int index){ if(index==9){ return arr[index];//相当于返回最后一个指针为NULL的结点的值 }else{ int m = getMax(arr,index+1);//递归求解后边的结点最大值 if(m>arr[index]){ return m;//这里可以看成在某一层返回来的最大值 }else{ return arr[index]; } } } int a[10]={1,3,2,11,21,4,44,23,54,12}; int t=0; cout<<getMax(a,t);
根据括号表示的二叉树的字符串创建二叉树
void createBtree(char *str,BtreeNode *&tree){ BtreeNode *bs[MaxSize],*p=NULL;//定义一个数组用于保存树的结点 *p指向保存当前进栈结点 tree=p;//空树 int index = 0;//串的索引 int top = -1;//栈的索引 char ch = str[index];//指向第一个字符 while(ch!='�'){//但字符串还没遍历完就继续遍历 switch(ch){ case '(':k=1,top++,bs[top] = p;break;//遇到左括号 k=1 且结点进栈 case ',':k=2;break;//表示接下来的结点是右孩子 case ')':top--;break;//表示当前栈顶的元素没有孩子结点 default://遇到数值表示出现孩子结点 //先创建一个结点用于保存数值 p = (BtreeNode *)malloc(sizeof(BtreeNode)); //先判断当前是否已经有双亲结点进栈 防止这个是根结点情况 可能情况a() (a(a,b)) if(tree == NULL){//这个判断只经过一次 tree = p;//表示当前这个结点是根节点 后边的元素均为该节点的子孙结点 }else{ switch(k){ case 1:bs[top]->leftChild=p;break;//左孩子 case 2:bs[top]->rightChild=p;break;//右孩子 } //此时不会直接将栈顶的元素出栈因为可能接下来还会有右孩子或者 孩子还有孩子 //此时当前的 } ; } index++; ch = str[index]; } }
javascript实现
function BtreeNode(){ this.left = null; this.right = null; this.data = null; } function createTree(str){ var Btree = null;//一个空二叉树 var arr = [];//用一个数组表示栈 var top = 1;//指向栈底 var p = null; var k; Btree = p; var index = 0;//字符串的索引 while(index<str.length){ switch(str[index]){ case '(':arr.push(p),k=1;break; case ',':k=2;break; case ')':arr.pop();break; default: p = new BtreeNode(); p.data = str[index]; if(Btree == null){ Btree=p; }else{ switch(k){ case 1:arr[arr.length-1].left = p;break; case 2:arr[arr.length-1].right = p;break; } } ; } index++; } return Btree; } var str = "1(2(9,3(7,0)),4(6,8))"; console.log(createTree(str));
效果:
