python信用评分卡建模(附代码,博主录制)
(十四)深度神经网络模型用于评分卡模型(理论)
https://blog.csdn.net/LuYi_WeiLin/article/details/88429879转载
本篇文章主要讲解以下两个内容
- 神经网络的概述
- 深度神经网络模型用于违约概率预测(代码实现看下一篇博客)
神经网络的概述
什么是人工神经网络

神经网络算法的核心:计算的过程、连接的结构、评估的工作、纠错的反馈、疯狂培训(不断运行)

人工神经网络的类型
神经元的特征:并非简单的相加,有相应的输出函数
学习规则:使得模型输出与标签尽量一致,不断去调整偏置因子和权重
其中下面的Hopfield网络、波尔兹曼机、适应谐振理论是物理学科衍生出来的神经网络模型
截止目前其实已经达到上百种神经网络模型了

最简单的人工网络模型:单层感知机器
单层感知器只能处理线性可分的情况
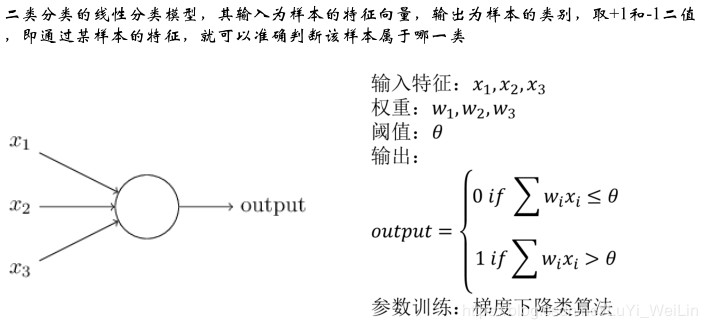
常见的激励函数
Sigmoid:无论x输入什么,输出属于(0,1)
Tanh(双曲正切):无论x输入什么,输出属于(-1,1)。Tanh(x)=2*Sigmoid(2*x)-1
Softplus:Softplus(x)=log(1+e^x),函数逼近于Relu函数,
有了Relu为什么要引进Softplus?因为Softplus函数性质优于Relu
Relu(整流器 Rectifier Liner Units):x输入小于0,输出为0;x输入大于等于0,输出x
在随机梯度下降中比Sigmoid和Tanh快,但是Relu很脆弱,很容易挂掉
二进制(线性分类中使用):当x小于0为0,x大于等于0为1
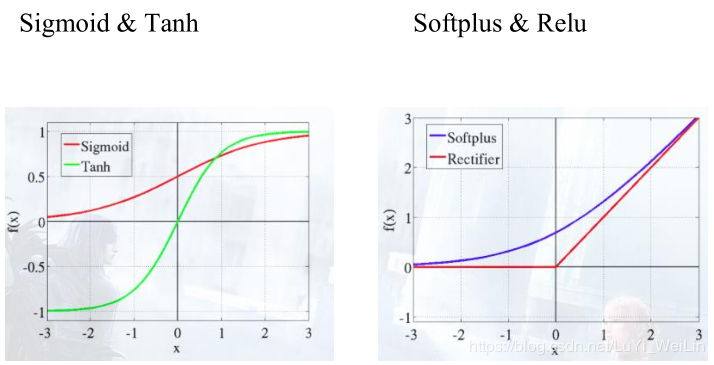
损失函数
损失函数其实不属于神经网络一部分,损失函数是预测输出值与真实值差了多少
构建神经网络,估计模型参数要借助损失函数,看输出值与真实值差了多少,反过去调整权重及参数(反向传播法【传播的是误差】基于链式法则),使用的是梯度下降法调整参数
为什么是反向,因为误差传递反向与信息传递方向相反
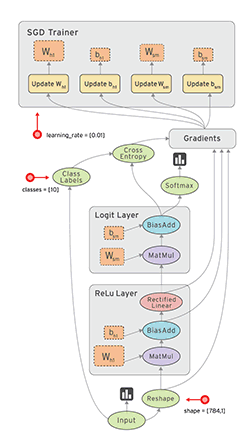

前馈型多层感知器
深度神经网络模型,深度的意思就是有多层隐藏层

深度神经网络模型用于违约概率预测
数据预处理
ANN模型对数据要求高
不能有缺失值:缺失值可以使用K-means、混合高斯分布、MCMC进行填补,或者剔除
移除常量型的特征:减少计算量、防止梯度流失
不能接受非数值形式输入,字符型变量需要编码
独热(One hot)编码
Dummy编码(哑变量编码):缺点是对于测试集中在训练集没有出现的数据无能为力
浓度编码:之前提及的badrate编码
变量归一化/标准化:输入特征尺度差异容忍很差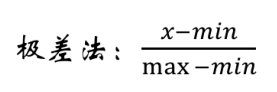
Z均值法:数值减去平均值,再除以其标准差,得到均值为0,标准差为1的服从标准正态分布的数据。
极差法和Z均值法容易受到极值的影响,剔除极值
什么是变量的归一化/标准化/中心化可以查看下面的链接
http://www.datasoldier.net/archives/505



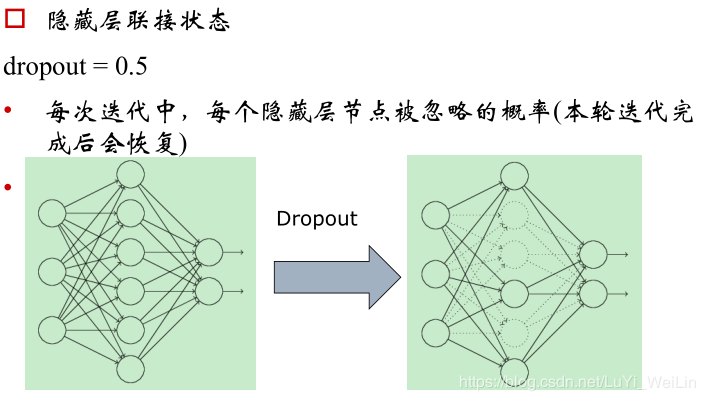
隐藏层连接状态并非全连接,避免过拟合以及减少计算量
学习率learning rate

迭代次数

模型的效果

人工神经网络的优缺点

在文章后,汇总一些有关神经网络模型用于评分卡模型问题:
首先评分卡模型到底能不能用神经网络模型来建立模型呢?
神经网络模型的优点就是模型准确度高,但是解释性不强。像申请评分卡、行为评分卡、催收评分卡一般需要在业务上可解释,一般不常用神经网络模型去建立模型,而像反欺诈模型不太需要可解释性,可以使用神经网络模型来建立模型。
神经网络模型只有最终输出的值有意义吗?
不单单是输出的信息是有用的,中间的隐藏层值可能也是有用的,但是对于前馈型神经网络,数据流入流出是单向的,包含的信息就少一点。但是RNN和AutoEncoder的话,中间的隐藏层值包含的信息量是丰富的,还可以从中提取新特征值
激活函数一般有什么要求吗?
激活函数除函数为0之外,其他地方要求可导
激活函数的导数不能是发散的,影响计算的稳定性
激活函数的导数不能太敏感,x变化一点点,整个偏导数不应有很大的变化
不能出现梯度消失的情况,梯度消失就导致梯度下降法不起作用了(信息传递方向与误差传递方向相反,因为只有输出才通过损失函数计算出误差,之后通过梯度下降法调整权重)
激活函数单调性,这样保证单层神经网络是凸函数,多层网络输出也是凸函数,凸函数在最优化上容易解决
激活函数输出值范围有限,这样梯度优化的方法更加稳定
激活函数最好为非线性,能实现非线性划分
隐藏层必须的吗?隐藏层一定要全连接吗?其加入有什么作用?
非必须;不一定要全连接;提高模型稳定性以及预测精度
python风控建模实战lendingClub(博主录制,catboost,lightgbm建模,2K超清分辨率)
https://study.163.com/course/courseMain.htm?courseId=1005988013&share=2&shareId=400000000398149
微信扫二维码,免费学习更多python资源