学校开设了 N 门的选修课程,每个学生可选课程的数量 M 是给定的。
学生选修了这 M 门课并考核通过就能获得相应的学分。
在选修课程中,有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其他的一些课程的基础上才能选修。
例如《Windows程序设计》必须在选修了《Windows操作基础》之后才能选修。
每门课的直接先修课最多只有一门。两门课可能存在相同的先修课。
你的任务是为自己确定一个选课方案,使得你能得到的学分最多,并且必须满足先修条件。假定课程之间不存在时间上的冲突。
输入格式
输入文件的第一行包括两个整数N、M(中间用一个空格隔开)其中1≤N≤300,1≤M≤N。
接下来N行每行代表一门课,课号依次为1,2,…,N。
每行有两个数(用一个空格隔开),第一个数为这门课先修课的课号(若不存在先修课则该项为0),第二个数为这门课的学分。
学分是不超过10的正整数。
输出格式
输出一个整数,表示学分总数。
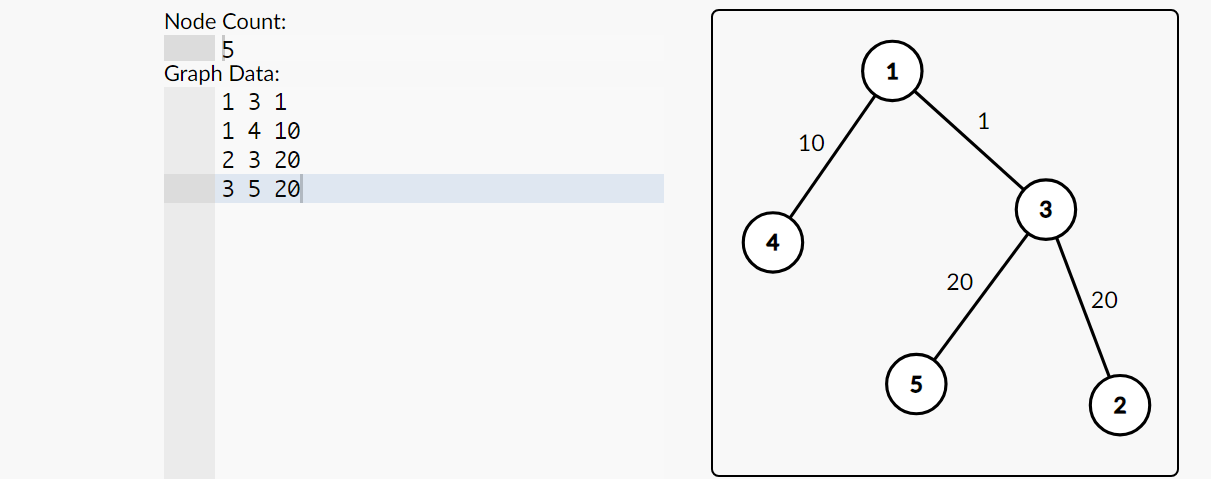
输入样例:
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
输出样例:
13
方法一:dp
这里可将课的看成重量为 1 的物品,对应的价值就是其学分,再利用分组背包思想;由于入度为 0 的先修课(节点)没有父节点,而这些课又必须上,故增加一个虚拟结点 0,0 指向这些入度为 0 的结点,且结点 0 的学分为 0
- 定义状态:
- f[i][j] 表示以 i 为根选 j 门课时收获的最大学分
- 思考初始化:
- f[...][...]=0
- 思考状态转移方程:
- f[i][j] = max{f[i][j], f[i][k]+f[son_i][j-k]},j∈[0,m),k∈[1,j);以 i 为根的子树要选 j 门课的最大学分等于 i 的子树选 j 门,加上从 son_i 的及其子树中选 j-k 门课的最大学分
- 思考输出:f[0][m]
#include<bits/stdc++.h>
using namespace std;
const int N=305;
int n,m,v[N],f[N][N];
vector<int> g[N];
void dfs(int u) {
for (int v : g[u]) {
dfs(v);
for (int j=m; j>=1; j--)
for (int k=1; k<=j; k++) {
f[u][j]=max(f[u][j], f[u][j-k]+f[v][k]);
}
}
for (int j=m; j>=1; j--) f[u][j]=f[u][j-1]+v[u]; //选u这门课
}
int main() {
std::ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
for (int i=1; i<=n; i++) {
int p; cin>>p>>v[i];
g[p].push_back(i);
}
m++;
dfs(0);
cout << f[0][m];
return 0;
}
复杂度分析
- Time:\(O(nms)\),
- Space:\(O(m)\),
二、苹果树
有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有1个儿子的结点)
这棵树共有N个结点(叶子点或者树枝分叉点),编号为1-N,树根编号一定是1。
现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量,求出最多能留住多少苹果。
f[i][j] 表示保留以i为根的子树的j条树枝可以留下来多少苹果,那么假如i保留了p条树枝,则i的子节点只能保留q-p-1条(q是最终需要保留的树枝数),减1是因为选择了 \(i->son_i\) 这一条
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105;
struct node{
int u,w;
};
vector<node> g[N];
int n,q,vis[N],f[N][N];
void dfs(int u) {
vis[u]=1;
for (auto& to : g[u]) {
int v=to.u, w=to.w;
if (vis[v]) continue;
dfs(v);
for (int j=q; j>=1; j--)
for (int k=0; k<j; k++) {
f[u][j]=max(f[u][j], f[u][j-k-1]+f[v][k]+w);
}
}
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n>>q;
for (int i=0; i<n; i++) {
int a,b,c; cin>>a>>b>>c;
g[a].push_back({b,c}), g[b].push_back({a,c});
}
dfs(1);
cout<<f[1][q];
return 0;
}
三、树
他从树中删除任意数量(可以为 00)的边,计算删除后所有连通块大小的乘积,L 将得到这么多的分数。
你的任务就是对于一颗给定的树,求出 L 能得到的最大分数。
输入格式
第一行一个整数 nn,表示树的节点个数。
接下来 (n-1)(n−1) 行,每行两个整数 u, vu,v,代表存在一条连接 u, vu,v 的边。
输出格式
输出一行一个整数,表示 L 能得到的最大分数。
四、树上染色
有一棵点数为 n 的树,树边有边权。给你一个在 0∼n 之内的正整数 k ,你要在这棵树中选择 k 个点,将其染成黑色,并将其他 的 n−k 个点染成白色。将所有点染色后,你会获得黑点两两之间的距离加上白点两两之间的距离的和的受益,问受益最大值是多少。
f[u][j]=max(f[u][j], f[u][j-k]+f[v][k]+val),大同小异的题,难点在于如何计算这个 val(白点两两之间的距离+黑点两两之间的距离)