概率分布与马尔科夫链的关系讨论2018年6月24日
22:38Copyright © 2018 Lucas Yu
小编原创,任何形式传播(转载或复制),请注明出处,谢谢!
摘要:
本文主要讨论使用一个简单的例子,采用实证的方式来讨论一般概率分布与马尔科夫链的关系,将二者联系起来。读者有一定概率论和随机过程基础会对理解有帮助。涉及内容包括:伯努利分布、伯努利过程以及马尔科夫链等。
本文的研究方法步骤:先确定研究单元(研究对象,它决定了研究的粒度和层级),然后才去讨论其相关性质。对象域确定很重要,以便明确目标,就像物体运动的研究不会去讨论物体的化学性质一样;论证方式采用层层递进论证(由粒度决定),并争取从多角度讨论。
素材:先上一段代码,供后面使用,使用时解释。
基本概念
伯努利分布:又名两点分布或者0-1分布,是一个离散型概率分布。若伯努利试验成功,则伯努利随机变量取值为1;若伯努利试验失败,则伯努利随机变量取值为0。记其成功概率为p,则失败概率为
1 − p。
(baidu 2018)
伯努利过程:是一个由有限个或无限个的独立随机变量 X1, X2, X3 ,..., 所组成的离散时间随机过程,其中 X1, X2, X3 ,...,
满足如下条件:
对每个 i, Xi 等于 0 或 1;
对每个 i, Xi = 1 的概率等于 p.
换言之,伯努利过程是一列独立同分布的伯努利试验。每个Xi 的2个结果也被称为“成功”或“失败”。所以当用数字 0 或 1
来表示的时候,这个数字被称为第i个试验的成功次数。
与伯努利过程相关的随机变量有:
前 n 个试验的成功次数服从二项分布。
要得到 r 次成功所需要的试验次数服从负二项分布。
要得到 1 次成功所需要的试验次数服从几何分布,这是负二项分布的一个特例
(zh.wikipedia 2018)
伯努利分布及过程研究
首先确定一次抛掷硬币试验为基本研究对象,该试验涉及到的随机变量包括伯努利随机变量(随机变量是个映射):
遂获取多个研究单元,即重复多次抛掷试验,统计多次试验结果,通过试验的方式研究随机变量的统计性质。
实证试验:
<1> 假设我们对硬币一无所知,只是不停的抛掷硬币;根据试验结果记录随机变量的值; 计算统计量。
<2> 绘制随机变量的分布图,并由分布计算一些统计量。
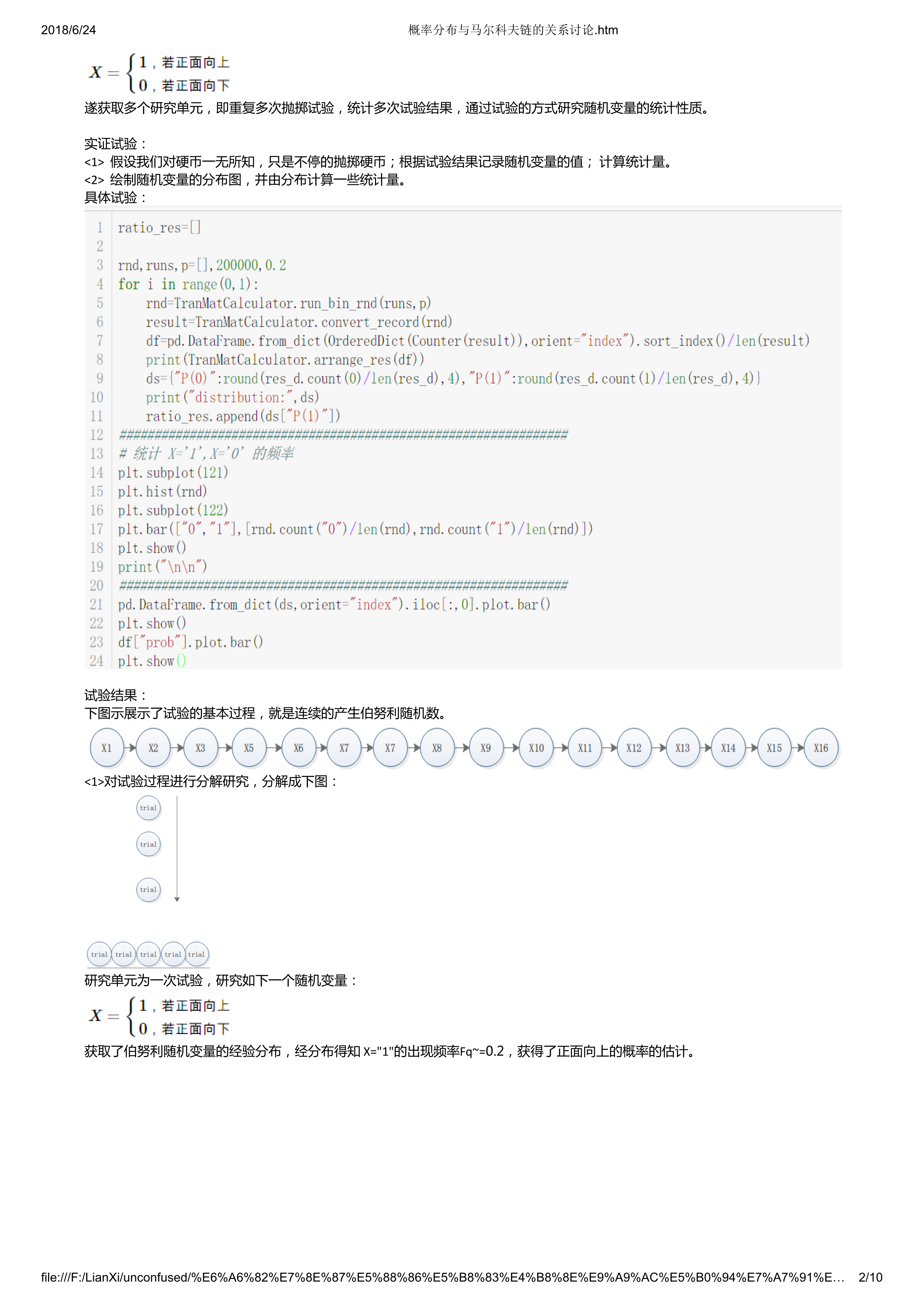
具体试验:
试验结果:
下图示展示了试验的基本过程,就是连续的产生伯努利随机数。
<1>对试验过程进行分解研究,分解成下图:
研究单元为一次试验,研究如下一个随机变量:
获取了伯努利随机变量的经验分布,经分布得知 X="1"的出现频率Fq~=0.2,获得了正面向上的概率的估计。
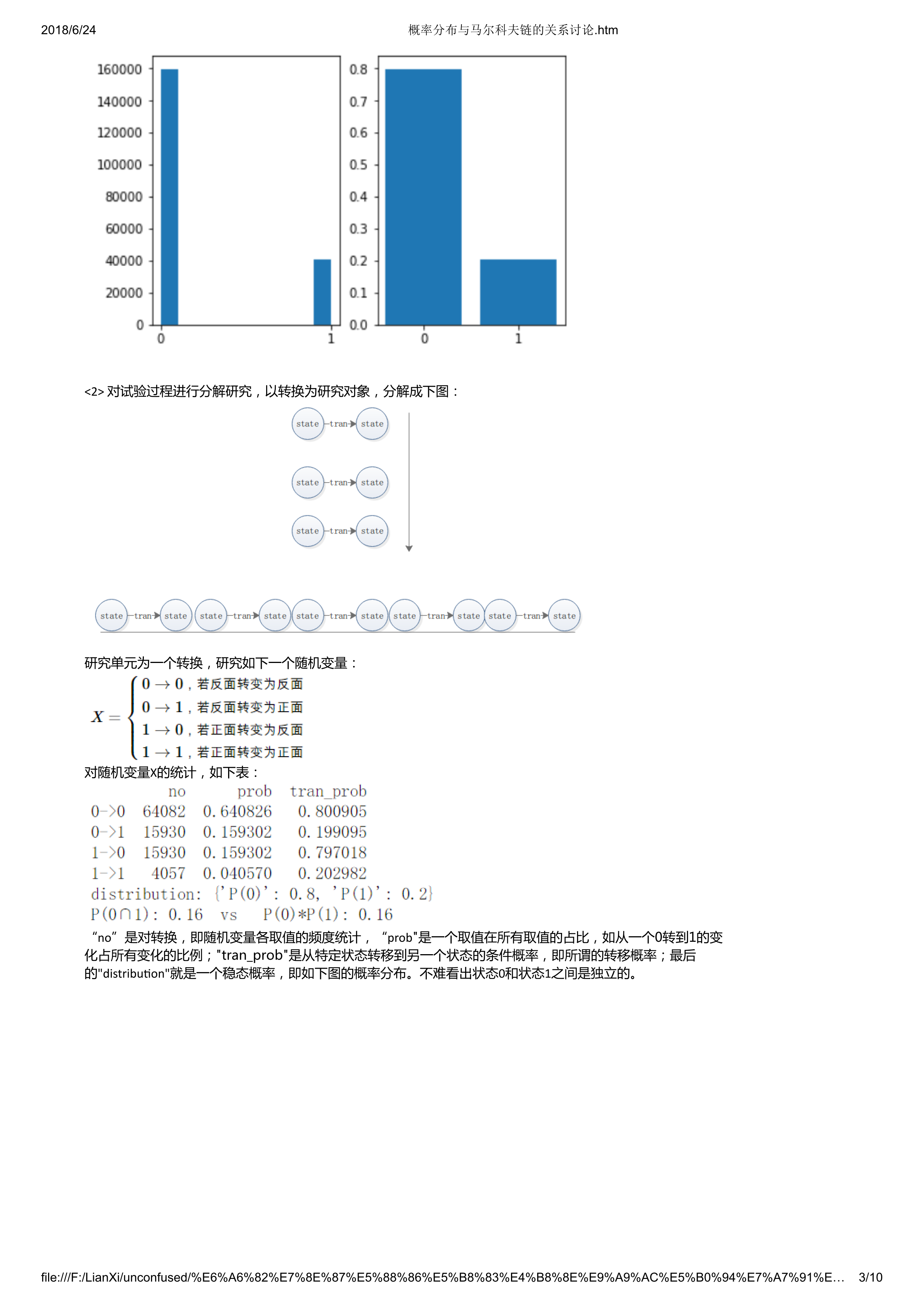
<2> 对试验过程进行分解研究,以转换为研究对象,分解成下图:
研究单元为一个转换,研究如下一个随机变量:
对随机变量X的统计,如下表:
“no”是对转换,即随机变量各取值的频度统计,“prob"是一个取值在所有取值的占比,如从一个0转到1的变化占所有变化的比例;"tran_prob"是从特定状态转移到另一个状态的条件概率,即所谓的转移概率;最后的"distribution"就是一个稳态概率,即如下图的概率分布。不难看出状态0和状态1之间是独立的。
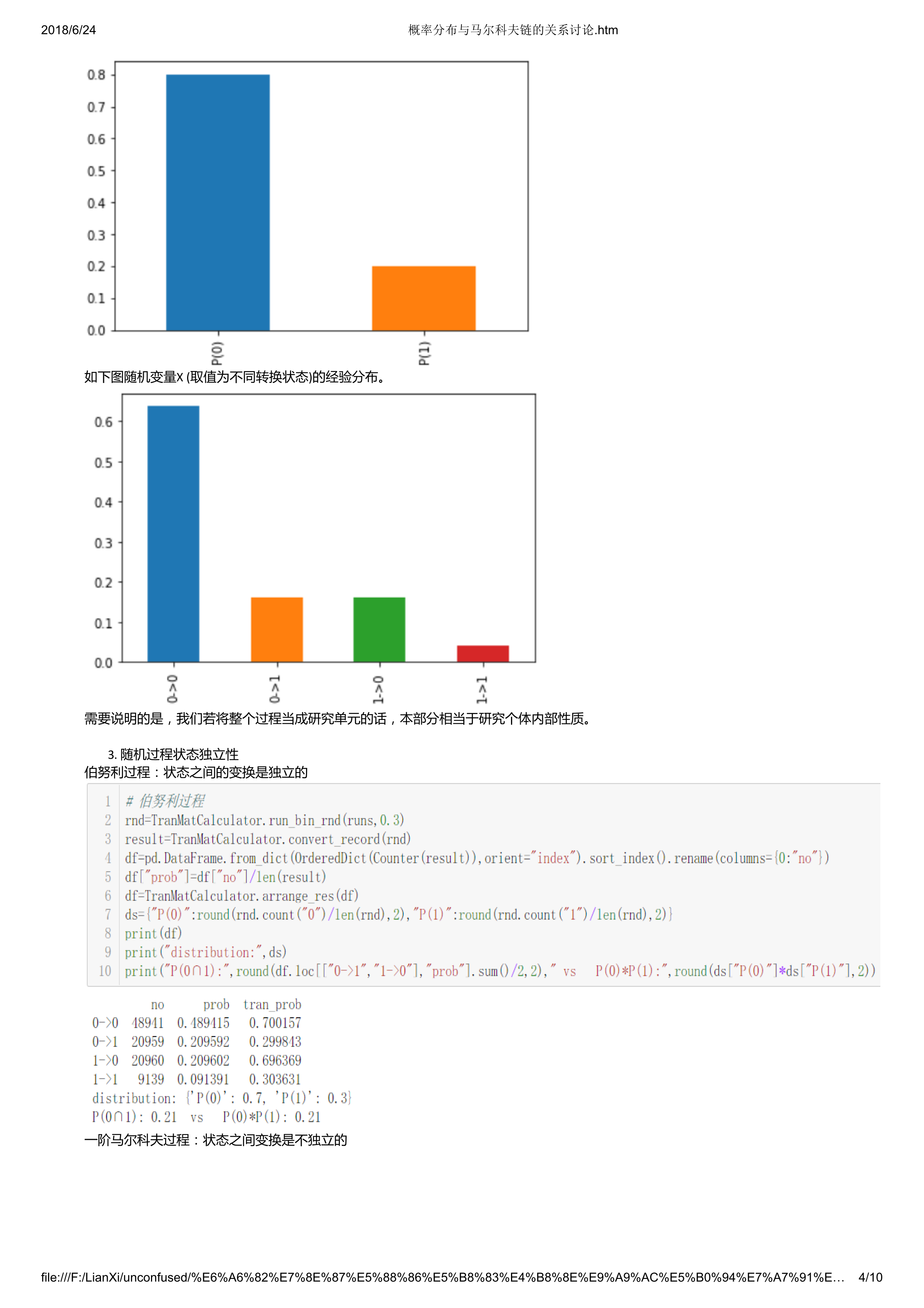
如下图随机变量X (取值为不同转换状态)的经验分布。
需要说明的是,我们若将整个过程当成研究单元的话,本部分相当于研究个体内部性质。
随机过程状态独立性
伯努利过程:状态之间的变换是独立的
一阶马尔科夫过程:状态之间变换是不独立的
二阶马尔科夫过程 状态之间变换是不独立的
从上面的图可以看出完全不同的过程最终都可以达到相同的稳态概率分布,马尔科夫链阶不同,参数不同 ,最终都有可达到相同的稳态分布 distribution:
{'P(0)': 0.7, 'P(1)': 0.3}
。而且不同阶的马尔科夫链,都可以统计出,相同的一阶转移矩阵,这也就是说从转移矩阵看不能分辨出阶数目这种隐含信息。马尔科夫链中不同转移之间确实不独立。伯努利过程状态之间独立。
根据以上过程可以绘制出如下图,看到这种图不要想当然的认为就是马尔科夫过程,这只是一个概率图表示而已:
马尔科夫性验证
马尔科夫性的最终验证主要是仰赖定义。本次研究的基本对象就是一个个马尔科夫链的实例化对象;一条定义好的马尔科夫链可以产生许多链的实例,正如从一个确定的概率分布中可以抽取许多个样本实例一样,如运行多次
generate_chain(p1=0.25,p2=0.43,chain_len=100000),就可以产生多个链的实例,这与面向对象类与实例的关系相似,类可以实例化产生许多实例对象一样。通过分析实例对象达到对类的认识。
<1> 对于给定的研究单位,可研究其上的随机变量,本处以成功的次数为随机变量,很显然它符合一个二项分布。
本例选择长度为n=4的马尔科夫链来研究。
<2> 根据定义对以上三个过程的马尔科夫性进行验证。
马尔科夫链的核心假设是只要时刻n的状态为i,不论过去发生了什么,也不论链是如何到达状态i的,下一个时刻转移到状态j的概率就一定是转移概率 p_ij
。数学上,马尔科夫链的特征称为马尔科夫性质,即满足:对于任意时间n,对于任意的状态 i,j∈S,以及任意之前可能的状态序列 i_0,...,i_n-1,均有
P{X_n+1=j|X_n=i,X_n-1=i_n-1,...,X_0=i_0} = P{X_x+1=j|X_n=i} = p_ij
所以,下一个状态X_n+1的概率分布只依赖于前一个状态X_n
对于每个确定的状态i,有 sum(p_i1,p_i2,p_i3,...,p_im)=1
(2ed,Dimitri Bertsekas,2008)
以上性质就是下一个时间点的状态的取值只与当前时间点的状态的取值有关,与其他时间点无关;对象A,B无关,白话:就是不管你B怎么变,A不会受B影响而发生改变!
使用一个特定的马尔科夫链类,产生多个实例,并通过对实例的分析,来证实某个马尔科夫链是否具有某种性质(即某种不变形或共性或特征)
a.伯努利过程马尔科夫性验证
b.一阶马尔科夫过程马尔科夫性验证
c.二阶马尔科夫过程马尔科夫性验证
通过以上实证分析,根据定义伯努利过程具有马尔科夫性,可以说伯努利过程是马尔科夫链的特例,只是相关性为0的情形,也就是说伯努利过程具有马尔科夫链的性质,由于其特殊性,还具有马尔科夫链不具有的性质,它的性质条件更严格而已。可以通过定义来对不同马尔科夫链链进行分析,据此可知马尔科夫链的具体类型,一阶还是二阶,或者根本就不符简单的合马尔科夫模型。