递归函数和二分法查找

一.递归函数

　　递归函数：在一个函数里在调用这个函数本身。

　　递归函数如果不受到外力的阻止会一直执行下去。但是我们之前已经说过关于函数调用的问题，每一次函数调用都会产生一个属于它自己的

名称空间，如果一直调用下去，就会造成名称空间占用太多内存的问题，于是python为了杜绝此类现象，强制的将递归层数控制在了997.

def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)

　　未报错之前能看到的最大数字就是998.当然了，997是python为了我们程序的内存优化所设定的一个默认值，我们当然还可以通过一些手段去

修改它：

import sys
print(sys.setrecursionlimit(设定递归的最大深度))

二.二分法查找

　　二分查找算法也称折半查找，基本思想就是折半，和平时猜数字游戏一样，比如猜的数字时67，猜测范围是0-100，则会先猜测中间值50，

结果小了，所以就会从50-100猜测，中间值为75，结果大了，又从50-75猜测中间值，一直到猜中为止。因此，二分查找有一个限制就是原先数

组需要是一个有序数组.

　在列表l中查找数字66:　

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
具体思考流程如下:

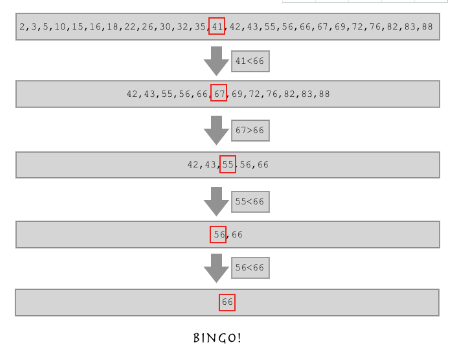
def func(l,aim):
    mid = (len(l)-1)//2
    if l:
        if aim > l[mid]:
            func(l[mid+1:],aim)
        elif aim < l[mid]:
            func(l[:mid],aim)
        elif aim == l[mid]:
            print("bingo",mid)
    else:
        print('找不到')
func(l,66)

运行结果:bingo 0

　　为什么没有找到66的索引呢?因为在比较得到比目标数大或者小的切片后,实际上是改变了目标的索引,切到最后只会出现0和1两种情况,说明上

述代码实现不了查找,需要优化.

l1 = [1, 2, 4, 5, 7, 9]
def two_search(l,aim,start=0,end=None):
    end = len(l)-1 if end is None else end
    mid_index = (end - start) // 2 + start
    if end >= start:
        if aim > l[mid_index]:
            return two_search(l,aim,start=mid_index+1,end=end)

        elif aim < l[mid_index]:
            return two_search(l,aim,start=start,end=mid_index-1)

        elif aim == l[mid_index]:
            return mid_index
        else:
            return '没有此值'
    else:
        return '没有此值'
print(two_search(l1,9))