在机器中采用"补码"表示带符号数(如果一个数是带符号的,那么,它在机器中就以补码表示,从某种表现上来说,补码可以说是"负数"的专利,因为,正数无所谓补码,至少,正数在其外观上面看不出是补码还是原码,而负数则不然.为了使思维不至于为相同的表示而感到混乱,就只要记住,补码只对负数起作用.当用到movsx的时候,会有一种有趣的现象:比如,对80h进行movesx的操作,我们得到的是0FF80h,显然,得到了一个负数,但前面的80h给人的感觉是一个正数,为什么带符号扩展就会得到一个负数呢?很简单,80h的符号位为1,在带符号数是它就是一个负数,是-102,之所以要用补码表示,很大程序上大概是因为原码的+0和-0分别是0000B和1000B的缘故吧,如果是补码,那么-0亦表示为0000B即+0的各位求反,末位加1,得到0000B,当然,对于+0是没有什么影响的,前面已经说了,补码在外观的表现上不对正数起作用.)如果是无符号数,那么原码,反码,补码就是相同的了.
1>正数的补码就是其本身
2>负数的补码是对其正数"各位求反,末位加1",如果是对负数本身而言,则应该是除符号位之外变反加1. 上述的"各位求反,末位加1"的操作称为求补. 在指令中用NEG表示,通过NEG,可以求得一个数的相反数.
3>正数的原码、补码、反码表示形式相同(这里,我觉得,仅仅是一个规定,没有运算法则或者说是运算规则来计算一个正数的补码或者反码,在实际操作的时候,看到正数,就直接写其原码即可,如果看到负数,那么,负数在机器中就要用补码来表示.注意的是,补码是机器对数字的表示,这样,会有一个很有意思的现象:正数和负数在机器用表示是一样的,比如说0EFh和-17d在机器中都用EF来表示.既然如此,其作运算的时候会是怎么样?(机器如何区分一个是正数还是负数?或者如何区分运算的结果是正数还是负数?这应该与CF和OF有关))
4>-10=0F6h=246 从这里推出:在8位二进制下,对于负数x(-128~-1)来说,存在下述等式: -x=256-|x| 这里的相等应该是指在机器中表示的时候是相同的表示形式
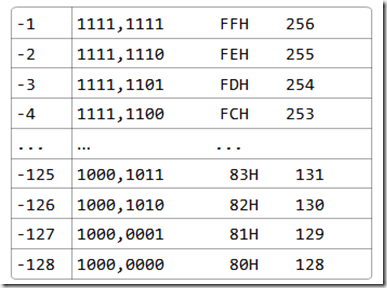
5>关于符号数与无等号数在机器中的表示(临界).依上面的方法,一个无符号数,显然,在机器中的表示就是其原码,不会有任何问题,比如一个字节可以表示0~255这256个数,0 是0000,0000,而255是1111,1111;但换作是符号数呢?首先来看正数(确切地说应该是非负数):从0~127,其最高位都是0(显然,最高位是符号位,而0就表示这是一个正数)其表示为0000,0000~0111,1111,换作是十六进制应该是00H~7FH;再来看负数,负数的表示范围是-128~-1(加上前面的0~125正好是256个数),-1的机器码为:1111,1111,换作十六进制为FFH(理解:-1在机器中以补码表示,-1的补码换如下求:首先,1的二进制表示为0000,0001,对其各位求反就得到了1111,1110,再对末位加1,就得到了FFH);再看一下-127,其机器码为1000,0001(127的原码为0111,1111,求反加1之后,得到81H);最后再来看128,不要以为128需要8位二进制表示,而在符号数中只有7位二进制可以表示数值,而是应该先写出128的原码为1000,0000,这样,对其求反,加1之后,自然可以得到1000,0000,即80H,这也恰恰说明了有符号数与无符号数在机器码上可以是完全相同的,但基意义完全不同.以下不妨写几个符号数的机器码:
之所以写这么多,是为了发现规律,从表中可以找到,负数的-1到负数的-128原来就是正数的256~到正数的128,其递减是同向的,也就是说,如果当作正数的无符号数来看,其是递减的,当作负数来看,其也是递减的