普通主席树
普通主席树比较简单 就是很多个权值线段树 每一次加进去log个节点(每层一个),剩下的节点用原来的线段树中的节点直接连到新节点上就好了
线段树
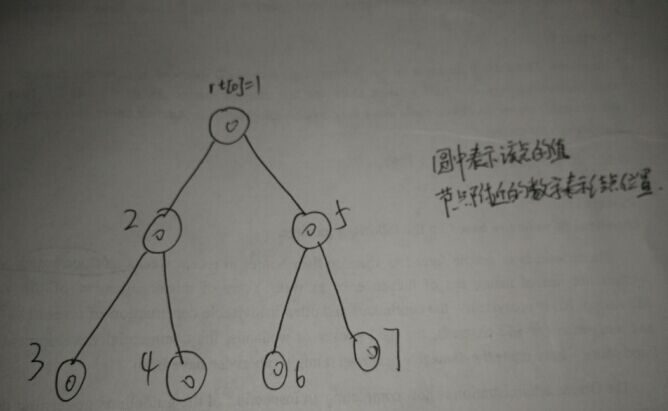
插入节点
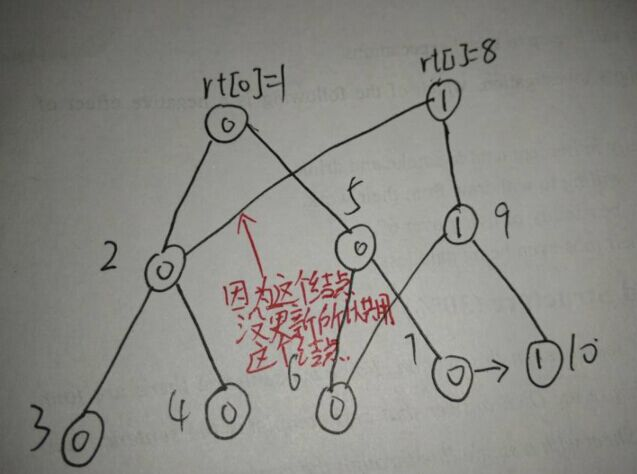
主席树

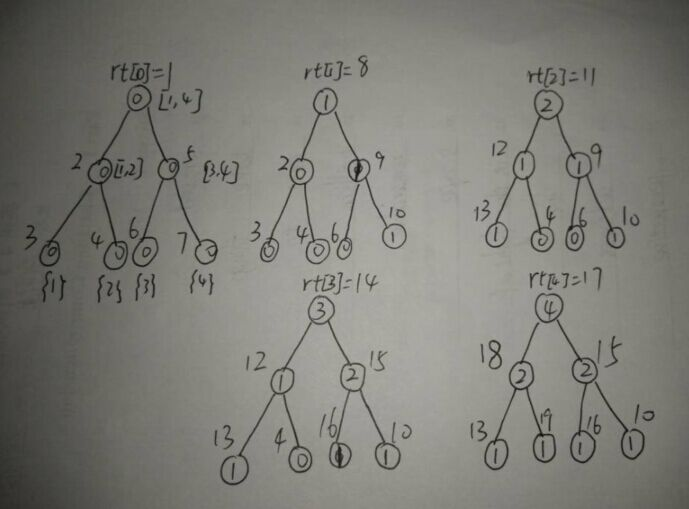
主席树拆开之后
POJ2104 主席树模板题 代码:

1 #include<algorithm> 2 #include<cstdio> 3 #include<vector> 4 using namespace std; 5 typedef long long ll; 6 7 ll read(){ 8 ll x=0,f=1;char c=getchar(); 9 while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();} 10 while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();} 11 return x*f; 12 } 13 14 const int maxn=100100,maxm=5050; 15 int n,m,cnt,nums; 16 int a[maxn],b[maxn],num[maxn],root[maxn]; 17 vector<int> vec; 18 struct Node{ 19 int l,r,val; 20 } tr[maxn*40]; 21 22 int getid(int x){return int(lower_bound(vec.begin(),vec.end(),x)-vec.begin())+1;} 23 24 void update(int l,int r,int &x,int y,int val){ 25 nums++;tr[nums]=tr[y];tr[nums].val++;x=nums; 26 if(l==r) return; 27 int md=(l+r)>>1; 28 if(val<=md) update(l,md,tr[x].l,tr[y].l,val); 29 else update(md+1,r,tr[x].r,tr[y].r,val); 30 } 31 int ask(int l,int r,int x,int y,int val){ 32 if(l==r) return l; 33 int md=(l+r)>>1; 34 int nw=tr[tr[y].l].val-tr[tr[x].l].val; 35 if(val<=nw) return ask(l,md,tr[x].l,tr[y].l,val); 36 else return ask(md+1,r,tr[x].r,tr[y].r,val-nw); 37 } 38 39 int main(){ 40 #ifdef LZT 41 //freopen("in","r",stdin); 42 #endif 43 n=read(),m=read(); 44 for(int i=1;i<=n;i++) 45 a[i]=read(),vec.push_back(a[i]); 46 sort(vec.begin(),vec.end());vec.erase(unique(vec.begin(),vec.end()),vec.end()); 47 for(int i=1;i<=n;i++) 48 a[i]=getid(a[i]),update(1,n,root[i],root[i-1],a[i]); 49 for(int i=1;i<=m;i++){ 50 int l=read(),r=read(),k=read(); 51 printf("%d ",vec[ask(1,n,root[l-1],root[r],k)-1]); 52 } 53 return 0; 54 }j 55 56 /* 57 7 3 58 1 5 2 6 3 7 4 59 2 5 3 60 4 4 1 61 1 7 3 62 */
可修改主席树
其实就是树状数组套主席树
为什么不能直接修改呢?
因为主席树的第i棵树是被第i+1到n棵树包含的
那么每次修改就得把后面的所有的树全部修改一遍
如果运气不好 复杂度可能达到$O(mn log n)
那么我们需要一个每个点可以通过log的时间算出来并且修改也只需log的时间的东西----->树状数组
ZOJ2112 Dynamic Rankings
这是一道可修改主席树的模板题
目前并没有看出来这个数据结构有什么应用 但是感觉很有用的样子
好像也可以cdq分治+整体二分做
这题比较卡内存 所以初值单独记录在一个线段树中 修改记录在树状数组中 查询的时候综合一下
时间复杂度: $O(M× log n× log n+n log n)$
代码:

1 //#pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<iostream> 3 #include<stdio.h> 4 #include<math.h> 5 #include <string> 6 #include<string.h> 7 #include<map> 8 #include<queue> 9 #include<set> 10 #include<utility> 11 #include<vector> 12 #include<algorithm> 13 #include<stdlib.h> 14 using namespace std; 15 #define eps 1e-8 16 #define pii pair<int,int> 17 #define inf 0x3f3f3f3f 18 #define rd(x) scanf("%d",&x) 19 #define rd2(x,y) scanf("%d%d",&x,&y) 20 #define ll long long int 21 #define mod 1000000007 22 #define maxn 60005 23 #define maxm 2500005 24 int m,n,nn,tot; 25 int a[maxn],f[maxn],T[maxn],S[maxn]; 26 int sum[maxm],l[maxm],r[maxm]; 27 int use[maxn]; 28 int h(int x){//该值在离散化后线段树的位置 29 return lower_bound(f+1,f+1+nn,x)-f; 30 } 31 void update(int pr,int lx,int rx,int v,int k){//插入,即新建第i个线段树 32 l[++tot]=l[pr];r[tot]=r[pr];sum[tot]=sum[pr]+k; 33 if(lx==rx) return; 34 int mid=(lx+rx)>>1; 35 if(v<=mid) { 36 l[tot]=tot+1; 37 update(l[pr],lx,mid,v,k); 38 } 39 else { 40 r[tot]=tot+1; 41 update(r[pr],mid+1,rx,v,k); 42 } 43 } 44 void build(int rt,int lx,int rx){//初始化空树 45 sum[rt]=0; 46 if(lx==rx) return; 47 l[rt]=++tot; 48 int mid=(lx+rx)>>1; 49 build(tot,lx,mid); 50 r[rt]=++tot; 51 build(tot,mid+1,rx); 52 } 53 int lowbit(int x){return x&(-x);} 54 int Sum(int x){ 55 int res=0; 56 for(int i=x;i;i-=lowbit(i)) res+=sum[l[use[i]]]; 57 return res; 58 } 59 void add(int x,int v,int k) 60 { 61 int tt; 62 for(int i=x;i<=n;i+=lowbit(i)){ 63 tt=S[i]; 64 S[i]=tot+1; 65 update(tt,1,nn,v,k); 66 } 67 } 68 69 int query(int L,int R,int k){ 70 for(int i=L-1;i;i-=lowbit(i)) use[i]=S[i];//use记录要操作的线段树下标 71 for(int i=R;i;i-=lowbit(i)) use[i]=S[i]; 72 int lx=1,rx=nn; 73 int lt=T[L-1],rt=T[R]; 74 while(lx<rx){ 75 int mid=(lx+rx)>>1; 76 int tmp=Sum(R)-Sum(L-1)+sum[l[rt]]-sum[l[lt]]; 77 if(k<=tmp){ 78 rx=mid; 79 for(int i=L-1;i;i-=lowbit(i)) use[i]=l[use[i]]; 80 for(int i=R;i;i-=lowbit(i)) use[i]=l[use[i]]; 81 lt=l[lt];rt=l[rt]; 82 } 83 else{ 84 lx=mid+1;k-=tmp; 85 for(int i=L-1;i;i-=lowbit(i)) use[i]=r[use[i]]; 86 for(int i=R;i;i-=lowbit(i)) use[i]=r[use[i]]; 87 lt=r[lt];rt=r[rt]; 88 } 89 } 90 return f[lx]; 91 } 92 char op[5]; 93 int q[10005][4],t; 94 int main() 95 { 96 rd(t); 97 while(t--){ 98 rd2(n,m); 99 for(int i=1;i<=n;i++) { 100 rd(a[i]);f[i]=a[i]; 101 } 102 nn=n; 103 for(int i=1;i<=m;i++){ 104 scanf("%s",op); 105 if(op[0]=='Q') { 106 scanf("%d%d%d",&q[i][1],&q[i][2],&q[i][3]); 107 q[i][0]=1; 108 } 109 else{ 110 scanf("%d%d",&q[i][1],&q[i][2]); 111 q[i][0]=0; 112 f[++nn]=q[i][2]; 113 } 114 } 115 sort(f+1,f+1+nn); 116 nn=unique(f+1,f+1+nn)-f-1;//离散化线段树,并去重 117 tot=0; 118 T[0]=0; 119 build(0,1,nn); 120 for(int i=1;i<=n;i++){ 121 T[i]=tot+1; //T[i]记录第i个线段树的根 122 update(T[i-1],1,nn,h(a[i]),1); 123 } 124 for(int i=1;i<=n;i++) S[i]=T[0]; 125 // int L,R,k,x; 126 for(int i=1;i<=m;i++){ 127 if(q[i][0]){ 128 printf("%d ",query(q[i][1],q[i][2],q[i][3])); 129 } 130 else{ 131 add(q[i][1],h(a[q[i][1]]),-1); 132 add(q[i][1],h(q[i][2]),1); 133 a[q[i][1]]=q[i][2]; 134 } 135 } 136 } 137 return 0; 138 }
