17.梯度下降

import numpy as np
import matplotlib.pyplot as plt

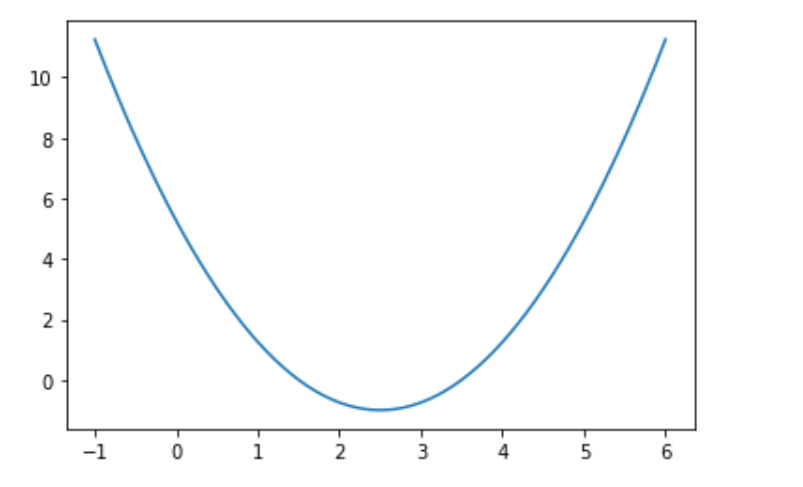
构造一元二次方程

x = np.linspace(-1, 6, 141)
y = (x-2.5)**2-1

绘图

plt.plot(x,y)

目标函数

def J(theta):
    try:
        return (theta-2.5)**2-1
    except:
        return float("inf")

目标函数的导数

def dJ(theta):
    return 2*(theta-2.5)

对于一个一元二次方程来讲，要寻找该方程的最小值，可以寻找方程导数为零的点。

如何寻找导数为零的点呢？以上面的方程：(theta-2.5)**2-1 为例

我们随便找一个点，

• 如果该点的导数为零，则一步找到
• 如果导数小于零，说明此时位于方程的左半边，需要向着x大于0的方向搜索
• 如果导数大于零，说明此时位于方程的右半边，需要向着x小于0的方向搜索

即：要使用梯度下降法找到一个函数的局部极小值，必须向着函数上当前点对应导数（或者是近似梯度）的反方点进行迭代搜索

方法一：

theta = 0.0
eta = 0.1
epsilon = 1e-8
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta-eta*gradient
    
    if (abs(J(theta)-J(last_theta)) < epsilon):
        break

print(theta)
print(J(theta)) 

2.499891109642585
-0.99999998814289

方法二：

theta = 0.0
eta = 0.1
epsilon = 1e-8
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta-eta*gradient
    
    if (abs(theta-last_theta) < epsilon):
        break

print(theta)
print(J(theta)) 

2.4999999646630586
-0.9999999999999988

以上可以看出两种计算方式效果是差不多的

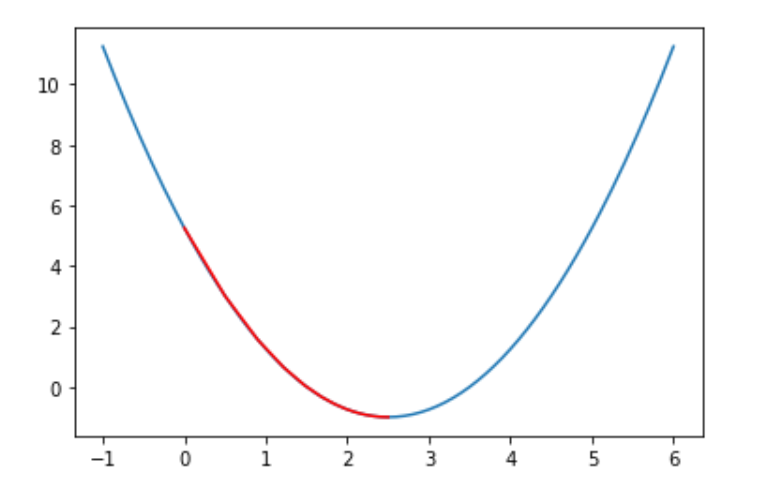
theta = 0.0
theta_history = [theta]
while True:
    gradient = dJ(theta)
    last_theta = theta
    theta = theta-eta*gradient
    theta_history.append(theta)
    
    if (abs(J(theta)-J(last_theta)) < epsilon):
        break

plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r")

len(theta_history)

46

def gradient_descent(initial_theta, eta, epsilon=1e-8):
    theta = initial_theta
    theta_history.append(inital_theta)
    
    while True:
        gradient = dJ(theta)
        last_theta = theta
        theta = theta-eta * gradient
        theta_history.append(theta)
    
        if (abs(J(theta)-J(last_theta)) < epsilon):
            break

def plot_theta_history():
    plt.plot(plot_x, J(plot_x))
    plt.plot(np.array(theta_history), J(np.array(theta_history)), color="r", marker="+")

eta = 0.01
theta_history = []
gradient_descent(0.0, eta)
plot_theta_history()

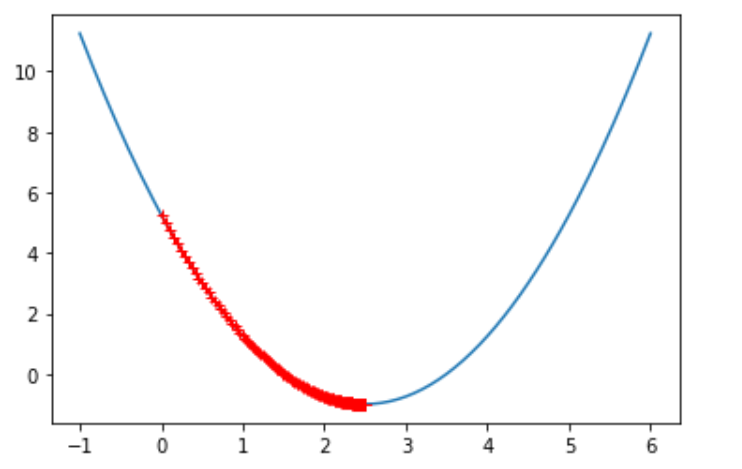
len(theta_history)

424

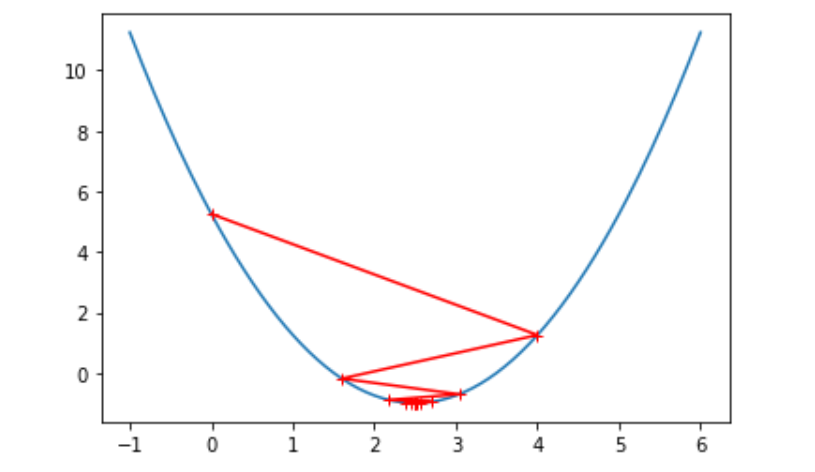
eta = 0.8
theta_history = []
gradient_descent(0.0, eta)
plot_theta_history()