(匈牙利算法) hdu 1281

棋盘游戏

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2757    Accepted Submission(s): 1612

Problem Description

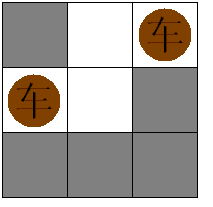
小希和Gardon在玩一个游戏：对一个N*M的棋盘，在格子里放尽量多的一些国际象棋里面的“车”，并且使得他们不能互相攻击，这当然很简单，但是Gardon限制了只有某些格子才可以放，小希还是很轻松的解决了这个问题（见下图）注意不能放车的地方不影响车的互相攻击。 
所以现在Gardon想让小希来解决一个更难的问题，在保证尽量多的“车”的前提下，棋盘里有些格子是可以避开的，也就是说，不在这些格子上放车，也可以保证尽量多的“车”被放下。但是某些格子若不放子，就无法保证放尽量多的“车”，这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点，你能解决这个问题么？

 

Input

输入包含多组数据， 
第一行有三个数N、M、K(1<N,M<=100 1<K<=N*M)，表示了棋盘的高、宽，以及可以放“车”的格子数目。接下来的K行描述了所有格子的信息：每行两个数X和Y，表示了这个格子在棋盘中的位置。

 

Output

对输入的每组数据，按照如下格式输出： 
Board T have C important blanks for L chessmen.

 

Sample Input

3 3 4 1 2 1 3 2 1 2 2 3 3 4 1 2 1 3 2 1 3 2

 

Sample Output

Board 1 have 0 important blanks for 2 chessmen. Board 2 have 3 important blanks for 3 chessmen.

 

Author

Gardon

 

Source

杭电ACM集训队训练赛（VI）

 

删边直接匈牙利算法求最大匹配，如果变小，那么说明这个位置符合条件

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
using namespace std;
int n,m,k,mark[105],mp[105][105],link[105];
struct node
{
    int x,y;
}e[105];
bool dfs(int x)
{
    for(int i=1;i<=m;i++)
    {
        if(mp[x][i]&&mark[i]==-1)
        {
            mark[i]=1;
            if(link[i]==-1||dfs(link[i]))
            {
                link[i]=x;
                return true;
            }
        }
    }
    return false;
}
int main()
{
    int cas=1;
    while(scanf("%d%d%d",&n,&m,&k)!=EOF)
    {
        int cnt=0;
        memset(mp,0,sizeof(mp));
        for(int i=1;i<=k;i++)
        {
            scanf("%d%d",&e[i].x,&e[i].y);
            mp[e[i].x][e[i].y]=1;
        }
        int maxx=0;
        memset(link,-1,sizeof(link));
        for(int i=1;i<=n;i++)
        {
            memset(mark,-1,sizeof(mark));
            if(dfs(i))
                maxx++;
        }
        for(int i=1;i<=k;i++)
        {
            int ans=0;
            mp[e[i].x][e[i].y]=0;
            memset(link,-1,sizeof(link));
            for(int i=1;i<=n;i++)
            {
                memset(mark,-1,sizeof(mark));
                if(dfs(i))
                    ans++;
            }
            mp[e[i].x][e[i].y]=1;
            if(ans<maxx)
                cnt++;
        }
        printf("Board %d have %d important blanks for %d chessmen.
",cas++,cnt,maxx);
    }
    return 0;
}