链接:https://ac.nowcoder.com/acm/problem/16697
来源:牛客网
题目描述
又到暑假了,住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场,分别位于一个矩形的四个顶点上,同一个城市中两个机场之间有一条笔直的高速铁路,第I个城市中高速铁路了的单位里程价格为Ti,任意两个不同城市的机场之间均有航线,所有航线单位里程的价格均为t。
图例(从上而下)
机场
高速铁路
飞机航线
注意:图中并没有标出所有的铁路与航线。
那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题,于是她来向你请教。
任务:找出一条从城市A到B的旅游路线,出发和到达城市中的机场可以任意选取,要求总的花费最少。
输入描述:
第一行为一个正整数n( 0 ≤ n ≤ 10 ),表示有n组测试数据。
每组的第一行有4个正整数S,t,A,B。
S( 0 < S ≤ 100 )表示城市的个数,t表示飞机单位里程的价格,A,B分别为城市A,B的序号,( 1 ≤ A,B ≤ S )。
接下来有S行,其中第i行均有7个正整数 xi1,yi1,xi2,yi2,xi3,yi3,Ti 这当中的(xi1,yi1),(xi2,yi2),(xi3,yi3)分别是第i个城市中任意3个机场的坐标,Ti 为第i个城市高速铁路单位里程的价格。
输出描述:
共有n行,每行1个数据对应测试数据(最小花费)。保留一位小数。
思路:
这道题难点在于整个图的建立和矩形第四个点的求解。
建图
在建图时我用(edge[])数组来存放该点的起点和终点,然后将其离散化缩为对应于(tot)的一个点,然后在数组(f[][])上更新其距离每个位置的边权。
第四个点
矩形给出的三个点是一个直角三角形,我找出最长的一条边,显然这条边是这个矩形的一条对角线,然后我取矩形的对角线的交点。
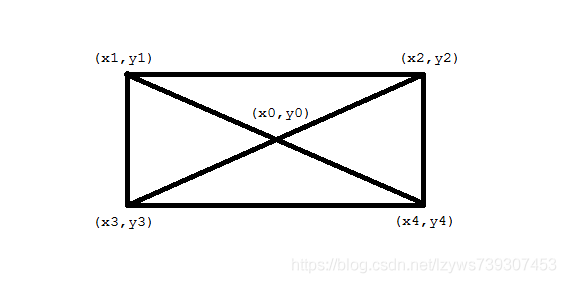
这个交点的坐标是直角三角形斜边的终点也即
[frac{x2+x3}{2}=x0quad frac{y2+y3}{2}=y0
]
[frac{x1+x4}{2}=x0quad frac{y1+1y4}{2}=y0
]
然后将两个式子联立:
[frac{x2+x3}{2}=frac{x1+x4}{2}quad ->quad x4=x2+x3-x1
]
其余的同理。
距离
直接(O(n^3))floyd就可以。
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define DOF 0x7f7f7f7f
#define endl '
'
#define mem(a,b) memset(a,b,sizeof(a))
#define debug(case,x); cout<<case<<" : "<<x<<endl;
#define open freopen("ii.txt","r",stdin)
#define close freopen("oo.txt","w",stdout)
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef pair<long long,long long> PII;
const int maxn = 2e5 + 10;
int xa,ya,xb,yb,xc,yc,cost,xd,yd;
int s,t,a,b;
double f[410][410],c[110];
struct force{
int id,x,y;
}edge[maxn];
double get_length(double x1,double y1,double x2,double y2){
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
int tot=0;
void get_edge(){
double dis1,dis2,dis3;
dis1=get_length(xa,ya,xb,yb);
dis2=get_length(xb,yb,xc,yc);
dis3=get_length(xa,ya,xc,yc);
if(dis1>dis2&&dis1>dis3){
xd=xa+xb-xc;yd=ya+yb-yc;
}else if(dis2>dis1&&dis2>dis3){
xd=xb+xc-xa;yd=yb+yc-ya;
}else if(dis3>dis1&&dis3>dis2){
xd=xa+xc-xb;yd=ya+yc-yb;
}
}
int main(){
// open;close;
int TT;scanf("%d",&TT);
while(TT--){
scanf("%d%d%d%d",&s,&t,&a,&b);
for(int i=0;i<=4*s;++i){
for(int j=0;j<=4*s;++j){
if(i==j)f[i][j]=0;
else f[i][j]=1e16;
}
}
for(int p=1;p<=s;++p){
scanf("%d%d%d%d%d%d%d",&xa,&ya,&xb,&yb,&xc,&yc,&cost);
c[p]=cost;
get_edge();
edge[++tot].id=p;
edge[tot].x=xa,edge[tot].y=ya;
edge[++tot].id=p;
edge[tot].x=xb,edge[tot].y=yb;
edge[++tot].id=p;
edge[tot].x=xc,edge[tot].y=yc;
edge[++tot].id=p;
edge[tot].x=xd,edge[tot].y=yd;
}
for(int i=1;i<=tot;++i){
for(int j=i+1;j<=tot;++j){
if(edge[i].id==edge[j].id){
f[i][j]=f[j][i]=get_length(edge[i].x,edge[i].y,edge[j].x,edge[j].y)*c[edge[i].id];
}else{
f[i][j]=f[j][i]=get_length(edge[i].x,edge[i].y,edge[j].x,edge[j].y)*t;
}
}
}
for(int k=1;k<=tot;++k){
for(int i=1;i<=tot;++i){
for(int j=1;j<=tot;++j){
if(f[i][j]>f[i][k]+f[k][j])
f[i][j]=f[i][k]+f[k][j];
}
}
}
double ans=1e16;
for(int i=(a-1)*4+1;i<=(a-1)*4+4;++i){
for(int j=(b-1)*4+1;j<=b*4;++j){
ans=min(ans,f[i][j]);
}
}
printf("%.1f
",ans);
}
}
参考博客:https://blog.csdn.net/lzyws739307453/article/details/85008349
