第四十五课 递归的思想与应用（下）

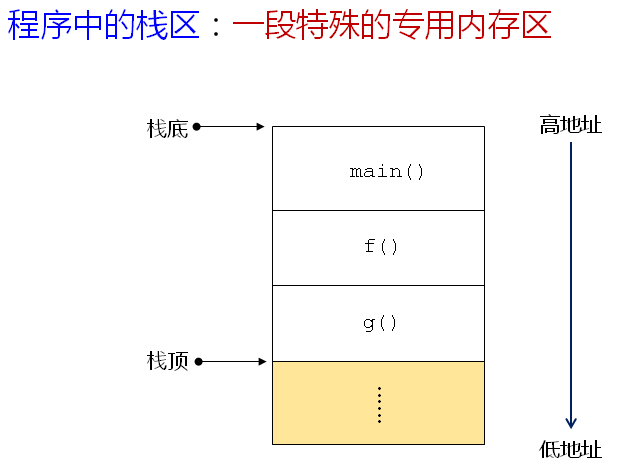
g函数返回后，f函数对应的栈中的数据没有任何变化，这就是回溯算法的核心。

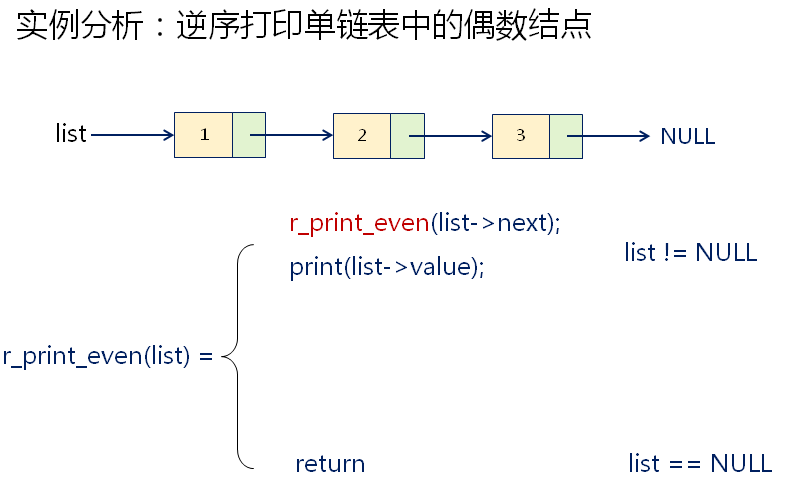
可以这样思考，先逆序打印从第二个节点开始的子表，最后再将第一个节点打印出来。

#include <iostream>
#include <cstring>
#include "DTString.h"

using namespace std;
using namespace DTLib;

struct Node
{
    int value;
    Node* next;
};

Node* create_list(int v, int len)  // v:数据元素从哪一个之开始。 len:长度
{
    Node* ret = NULL;
    Node* slider = NULL;

    for(int i=0; i<len; i++)
    {
        Node* n = new Node();

        n->value = v++;
        n->next = NULL;

        if( slider == NULL )
        {
            slider = n;
            ret = n;
        }
        else
        {
            slider->next = n;
            slider = n;
        }
    }

    return ret;
}

void destroy_list(Node* list)
{
    while( list )
    {
        Node* del = list;

        list = list->next;

        delete del;
    }
}

void print_list(Node* list)
{
    while( list )
    {
        cout << list->value << "->";

        list = list->next;
    }

    cout << "NULL" << endl;
}



void r_print_even(Node* list)
{
    if( list != NULL)
    {
        r_print_even(list->next);

        if( (list->value % 2) == 0 )
        {
            cout << list->value << endl;
        }
    }
}

int main()
{
    Node* list = create_list(2, 5);

    print_list(list);

    r_print_even(list);

    destroy_list(list);

    return 0;
}

 逆序打印栈的增长与退栈示意图：

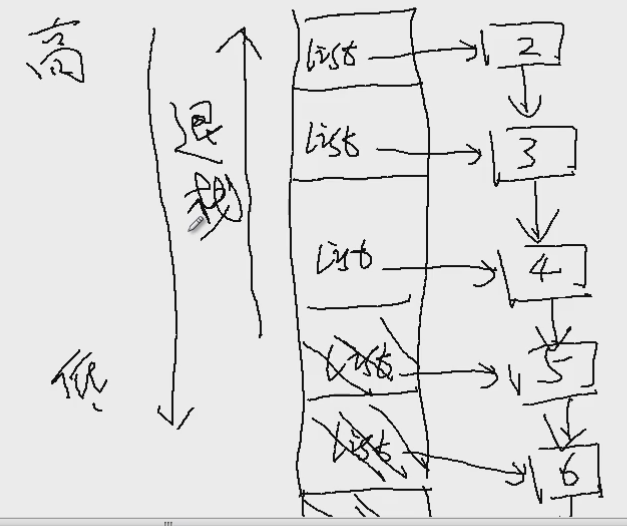
 退栈打印的过程就是回溯的过程。

 递归调用的时候只是先将参数保存在栈上，这时这个参数还没有用到，只是让指针指向了相应的节点，退栈的时候才用到。

类似于走迷宫，走到一个路口时先做个标记，这个标记暂时不用，回来的时候再用。根据标记找来时的路。

回溯的本质就是做标记，这样方便回退。

八皇后：

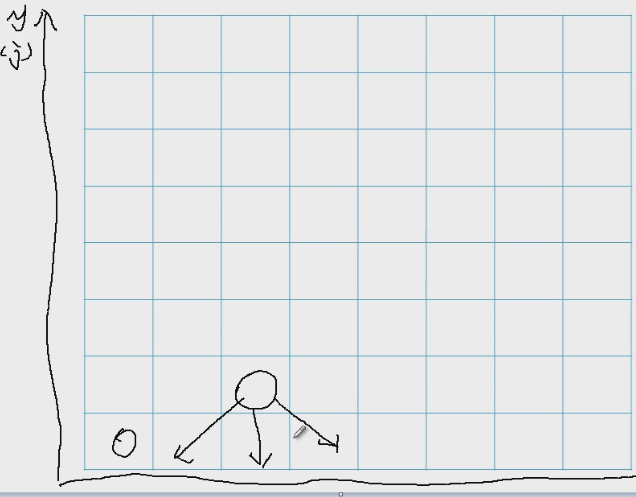
放皇后的时候只需要关注箭头的方向，因为其他的方向还没有放任何东西。

当我们发现某一行的任何一个位置都不能放皇后的时候，就开始要回溯了。因为，这证明了上一行放置皇后的地方是错误的。

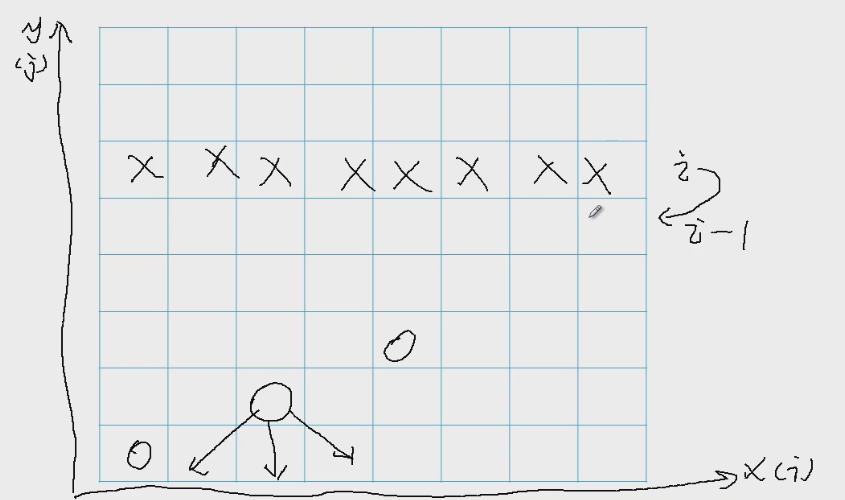
 当我们发现第i行的任何一个位置都不能放置皇后了，这就证明了第i-1行放置的位置是错误的。

如果发现第i-1行也没有地方可以放置皇后了，这意味着还要继续回退，退到i-2行，这就是回溯。

 

理论上，每放置一个皇后要判断8个方向，但是我们从第一行开始放置皇后，有规律的放，因此，只需要考虑三个方向。

如果判断一个位置的左下角对角线是否已经放置了皇后，那就在这个位置的基础上，在xy坐标上不断的减一。因此，方向数据很重要。左下角方向数据是(-1,-1)。

#include <iostream>
#include <cstring>
#include "DTString.h"
#include "LinkList.h"

using namespace std;
using namespace DTLib;

struct Node
{
    int value;
    Node* next;
};

Node* create_list(int v, int len)  // v:数据元素从哪一个之开始。 len:长度
{
    Node* ret = NULL;
    Node* slider = NULL;

    for(int i=0; i<len; i++)
    {
        Node* n = new Node();

        n->value = v++;
        n->next = NULL;

        if( slider == NULL )
        {
            slider = n;
            ret = n;
        }
        else
        {
            slider->next = n;
            slider = n;
        }
    }

    return ret;
}

void destroy_list(Node* list)
{
    while( list )
    {
        Node* del = list;

        list = list->next;

        delete del;
    }
}

void print_list(Node* list)
{
    while( list )
    {
        cout << list->value << "->";

        list = list->next;
    }

    cout << "NULL" << endl;
}



void r_print_even(Node* list)
{
    if( list != NULL)
    {
        r_print_even(list->next);

        if( (list->value % 2) == 0 )
        {
            cout << list->value << endl;
        }
    }
}

template <int SIZE>
class QueueSolution : public Object
{
protected:
    enum { N  = SIZE + 2};  //设置边界用

    struct Pos : public Object
    {
        Pos(int px = 0, int py = 0) : x(px),y(py){}
        int x;
        int y;
    };

    int m_chessboard[N][N];
    Pos m_direction[3];  //方向数组
    LinkList<Pos> m_solution; // 使用链表存储解决方案(放置皇后的位置)
    int m_count;

    void init()
    {
        m_count = 0;

        for(int i = 0; i < N; i+=(N-1))
        {
            for(int j = 0; j<N; j++)
            {
                m_chessboard[i][j] = 2;
                m_chessboard[j][i] = 2;
            }
        }

        for(int i=1; i<=SIZE; i++)
        {
            for(int j = 1; j <= SIZE; j++)
            {
                m_chessboard[i][j] = 0;
            }
        }

        m_direction[0].x = -1;
        m_direction[0].y = -1;
        m_direction[1].x = 0;
        m_direction[1].y = -1;
        m_direction[2].x = 1;
        m_direction[2].y = -1;
    }

    void print()
    {
        for(m_solution.move(0); !m_solution.end(); m_solution.next())
        {
            cout << "(" << m_solution.current().x << "," << m_solution.current().y << ") ";
        }

        cout << endl;

        for(int i=0; i<N; i++)
        {
            for(int j=0; j<N; j++)
            {
                switch(m_chessboard[i][j])
                {
                    case 0 : cout << " " ; break;
                    case 1 : cout << "#" ; break;  //有皇后
                    case 2 : cout << "*" ; break;
                }
            }

            cout << endl;
        }

        cout << endl;
    }

    bool check(int x, int y, int d)
    {
        bool flag = true;

        do
        {
            x += m_direction[d].x;
            y += m_direction[d].y;
            flag = flag && (m_chessboard[x][y] == 0);
        }
        while( flag );

        return (m_chessboard[x][y] == 2); //do while退出时，如果到达了边界说明这个方向没有皇后
    }

    void run(int j)  //检查第j行有没有可以放置皇后的位置
    {
        if( j <= SIZE )
        {
            for(int i = 1; i <= SIZE; i++)
            {
                if( check(i, j, 0) && check(i, j, 1) &&check(i, j, 2) )
                {
                    m_chessboard[i][j] = 1;

                    m_solution.insert(Pos(i, j));

                    run(j + 1); // 看下一行能不能放皇后，如果返回，意味着i，j位置不能放皇后，要回溯

                    m_chessboard[i][j] = 0;

                    m_solution.remove(m_solution.length() - 1);

                }
            }
        }
        else
        {
            //到这里意味着找到了解决方案
            m_count++;

            print();
        }
    }
public:
    QueueSolution()
    {
        init();
    }

    void run()
    {
        run(1);

        cout << "Total  : " << m_count << endl;
    }
};

int main()
{
    QueueSolution<8> qs;

    qs.run();

    return 0;
}

共92种解法。

小结：