分析一篇组里博士师姐的论文,我的基础方向和这篇一致,学习优秀的地方,提出一些建议和不同的想法。
《基于压力的行为传播与竞争模型》 2021-05-10,SCI 4区,IF:1.668
Abstract:The influence of node behavior by the relevant group behavior in complex networks is a topic of recent interest. In order to measure the direct and indirect influence of the neighborhoods, the behavioral propagation and competition model was established based on the pressure. The pressure is described by the impact of group behavior on nodes, which is related to the length and number of reachable paths between two nodes for measuring the nodal behavioral influence. In addition, the pressure range has an effect on the pressure. By modeling and analyzing the change of nodes motivation and the rules of behavioral propagation, and numerical simulations are performed on the small-world networks and the scale-free networks. The results show that pressure is the major factor in the node behavioral motivation, where the pressure generated from behavior in related group network is dependent on the relative location and number of participators. At the same time, network structure also plays an important role at behavior propagation process. Further, competition arises when multiple behaviors are spread among people, while winning behaviors are widely spread among people.
摘要:复杂网络中相关组行为对节点行为的影响是最近感兴趣的话题。为了衡量社区的直接和间接影响,建立了基于压力的行为传播和竞争模型。压力是通过组行为对节点的影响来描述的,它与两个节点之间可达路径的长度和数量有关,用于衡量节点行为影响。此外,压力范围对压力有影响。通过对节点动机变化和行为传播规律的建模分析,对小世界网络和无标度网络进行数值模拟。结果表明,压力是影响节点行为动机的主要因素,其中,相关群体网络中的行为所产生的压力取决于参与者的相对位置和数量。同时,网络结构在行为传播过程中也起着重要作用。此外,当多种行为在人们之间传播时,竞争就会出现,而获胜行为在人们之间广泛传播。
Introduction:
- Among numerous research fields of complex networks, behavioral propagation has been one of the hot spots
- For example: When the COVID-19 comes, some people wear masks to reduce the risk of being infected by the virus, their behavior would cause people around them to pay attention to protection, so they would wear masks and reduce travel. (以COVID-19时期戴口罩行为为例解释行为传播)
- Behavioral propagation is an important subfield of network science as an inevitable outgrowth of the need to understand how individual’s behavior has been changed by group behaviors
Literature review:
- Individual behavior is related to personal preference and group behavior
- Suh investigated the “retweeting” behavior as a mechanism for behavioral propagation and explored triggering condition associated with the powerful propagation ability of behavior
- Daley& Kendall proposed a DK model which defined three different states by the different individuals in the SIR model, ignorants, spreader, and stifler.
- Nicholas discovered that a person’s chance of becoming obese increased 40 percent if the person had a close friend who is an obese person. Similarly, smoking also has the same spread process by close and distant social ties, a person’s chance of smoking cessation increased 67 percent if the person had a smoking cessation spouse.
- McPherson revealed that the social relationship network in which people are placed are homogeneous, the individual within the homogeneous network have similar education, religion, and profession, his homogeneity allows them to have similar experiences and receive the same information, and have much the same attitude toward things.
- Nian revealed that people prefer to receive and forward messages sent by someone with better credibility when they are confronted with a message from different sources.
- Dong explained that people are more likely to spread negative information based on negative biases when they receive both positive and negative news.
- Hu proved the impacts of hub nodes on propagation dynamics, and looking for hub nodes with greater propagation capability by different algorithms in networks.
- Wang studied the sentiments in both posts and reposts which have positive impacts on information propagation.
Past researches have been devoted to solving the change of the network structure and the characteristics of nodes and edges for the impact of behavioral propagation, but the interaction of multiple neighbors in a group is not mentioned.
师姐在文献综述部分,列举了一系列网络结构的变化、节点和边的特征对于行为传播的影响,提出以往的这些研究并没有提及组中的多 个邻居节点的相互作用。(首先可以学习一些简单的英文的表述,但文献综述有一些局限,没有很强的逻辑联系,但是作为入门写作,可以采用这样的方式,我称之为列举法,①总结相关文献内容 ②提出它们相同点和共同的不足 ③引出自己的方向)
Goal:
- In this paper, the pressure of neighbors is introduced as a unique behavior motivation to describe the influence of group behavior on individuals. (单独变量)
- The behavioral propagation probability generated by group behavior to nodes is defined, discussing the phenomenon of behavioral propagation and competition, and quantizing the behavioral propagation probability through modeling, and discusses the propagation characteristics under different network structures and pressure. (本文主要要干的事情,但是英文描述极其不好)修改一下:We define the concept of the behavioral propagation probability generated by group behavior to nodes and study the phenomenon between propagation and competition. Through modeling, we also quantize the behavioral propagation probability and then discuss the propagation characteristics under different network structures and pressure.
- The Pressure-based SIR model --- PSIR
Modeling Behavioral Pressure:
- Definition 1-wi ,j represents the pressure between node vi and node vj
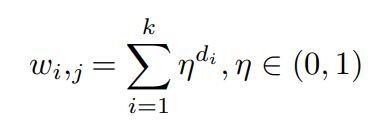
Where k represents the number of reachable paths from vj to node vi , and di represents the length of the i-th reachable path. η is a constant, set in 0.7 in this paper.
-
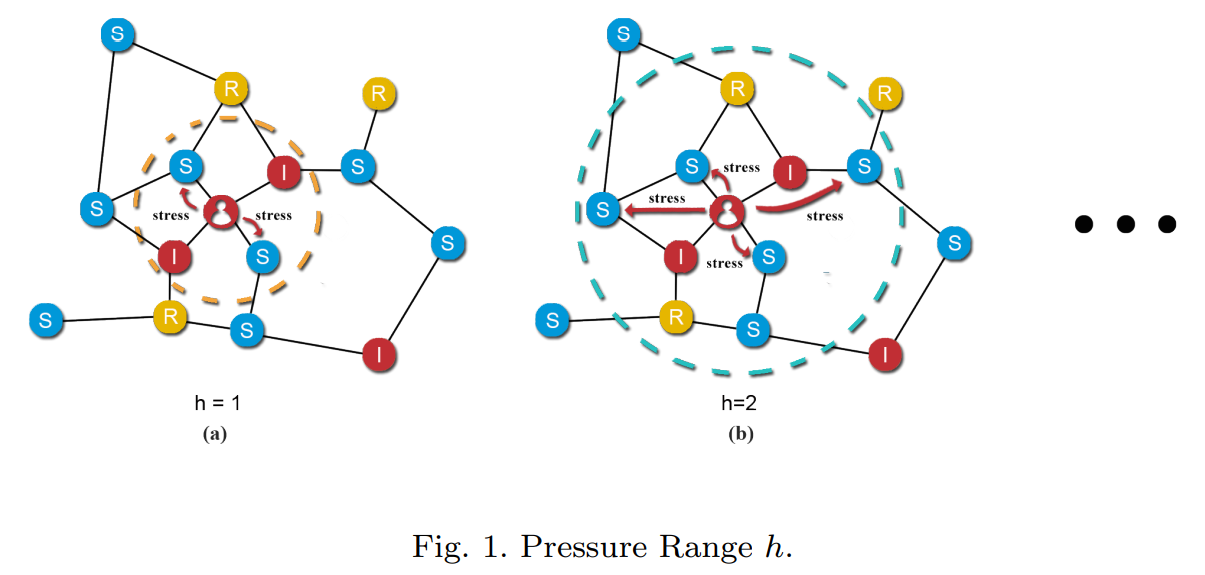
Definition 2-h = dmax represents the pressure range of node.
-
Hypothesis 1-If wi ,j → 0, k = 1, then di = dmax → +∞, that is, the pressure from vj to node vi decreases as the length of path increases, thus h = dmax, that is, pressure range is dmax.
-
Corollary 1-The pressure from vj to node vi is satisfied the equation below:

Where wi ,j is the pressure from vj to node vi , dmin is the length of shortest path from vj to node vi .In this paper,there is no significant interaction between the behavior of nodes when path length di ≤ 3. Thus, h = 2.
- Remark 1-Pressure range h is the path length that a node’s behavior can affect. h represents the frequency of communication and interaction within modes in a network. If the shortest path length between two nodes is greater than the pressure range h, the behavior of the two nodes will no longer affect each other.
System Model and Problem Formulation:
①Dynamic Participate Rate
- Definition 3-Θ(i, t) is the participate pressure of node vi at time stamp t.
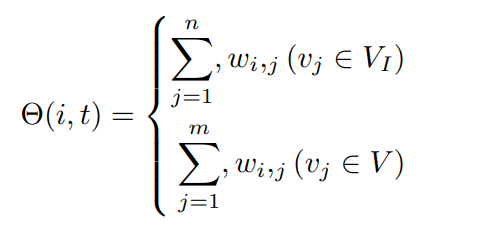
Here, n, m, separately represents the nodes number in VI and V , wi ,j represents the pressure from node vj to node vi .
-
Remark 2-Participate pressure refers to the motivation when an individual is influenced by the neighbors, and doubts and changes his own views and behavior, and keeps their behavior consistent with the group. (此处描述感觉很乱)修改一下:when an individual who is influenced by the neighbors doubts and changes his own views and behavior, and then keeps his behavior consistent with the group.
-
Definition 4-Θh(i, t) is the belonging pressure of node vi at time stamp t.
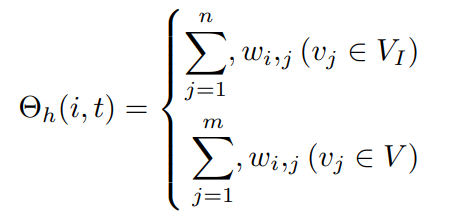
Here, node vi is an Ii node, where n, m separately represents the nodes number in Vi and V , wi ,j represent the pressure from node vj to node vi . Θh(i, t) = Θ(i, t) if the behavior has only one state.
- Definition 5-Ω(i, j, t) is the competition pressure between node vi and node vj at time stamp t.
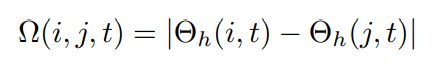
Where Θh(i, t) and Θh(j, t) separately represent the belonging pressure between node vi and node vj at time stamp t.
- Remark 3-The competition pressure is the behavior influence between two participators of different states for each other.

- Definition 6-β(i, t) is the participate probability of node vi participating in the behavior, which become the I node at time stamp t.
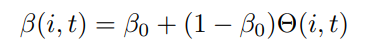
Here, β0 represents the initial participate probability. Θ(i, t) is the participate pressure of node vi at time stamp t.
- Remark 4-Participate probability is the participation motivation of behavior for one node, which is related to the value of the behavior itself and the pressure from neighbors.
- Definition 7-βh(i, j, t) is the competition probability between node vi and node vj at time stamp t.
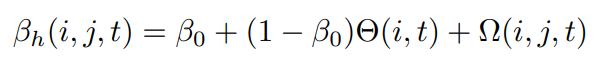
Where β0 represents the initial participate probability, Θh(i, t) represents the belonging pressure of node vi at time stamp t, Ω(i, j, t) represents the competition pressure between node vi and node vj at time stamp t.
- Remark 5-Competitive pressure refers to the probability that when two nodes are infected by different behaviors, the high-pressure node is applied to the low-pressure node to change the node state.
②Analysis of Pressure-based SIR model Propagation Characteristics
- differential equation based on PSIR model
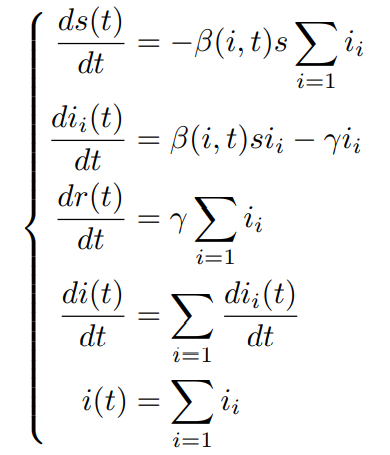
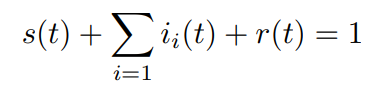
这里推导了传播阈值
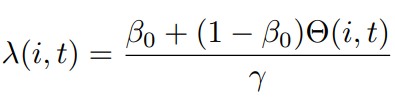
λ = 1 is the propagation threshold of the Pressure-based SIR model
-
If λ > 1, then γ = 0 means the behaviors have not spread;
-
If λ < 1, then γ > 0, and as the value increases, the value of r also increases, meaning that the range of behavioral propagation in the network also increases.
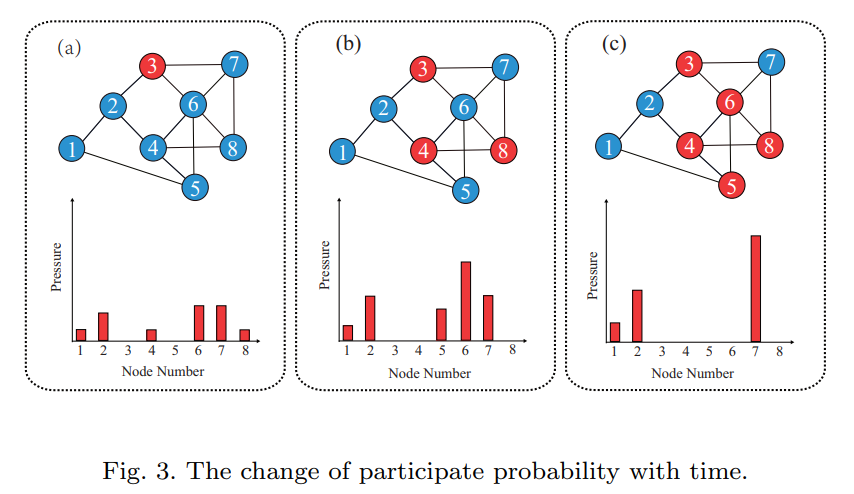
Simulation results:
The expressions are Gws(N, K, ζ) and Gba(N, K). In the formula, N = 10000, K = 4, ζ = 0.3, h = 2. (将模型代入WS和BA网络中)
-
The total number of nodes is N
-
The average degree of node is K
-
The random reconnection rate of the smallworld networks is taken as ζ
-
The number of the source node is taken as c
-
The pressure range is taken as h
①Simulation and Analysis of Pressure Influence on Behavioral Propagation
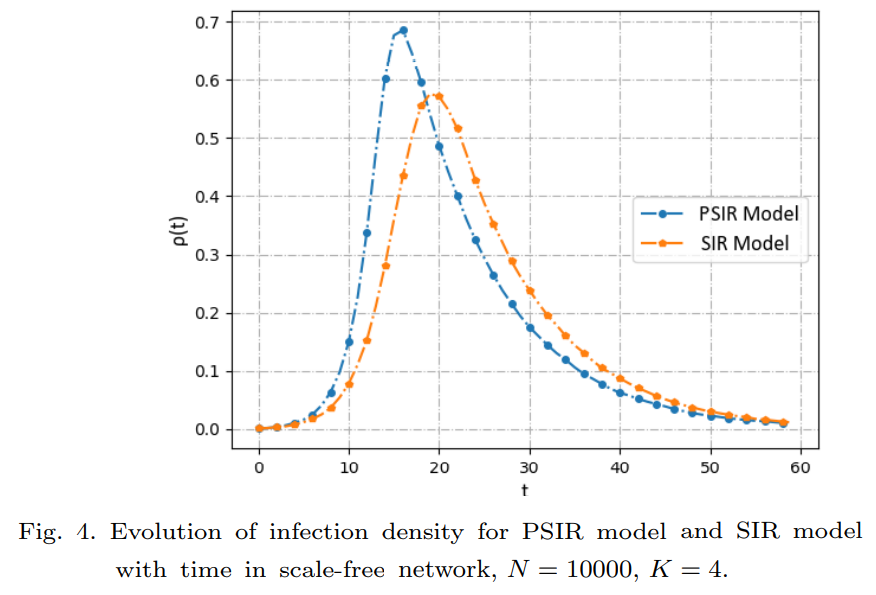
- there is a significant influence of pressure to promote the behavioral propagation in society. (the peak change of infection density)
②Simulation and Analysis of The Random Reconnection of Small-World Network
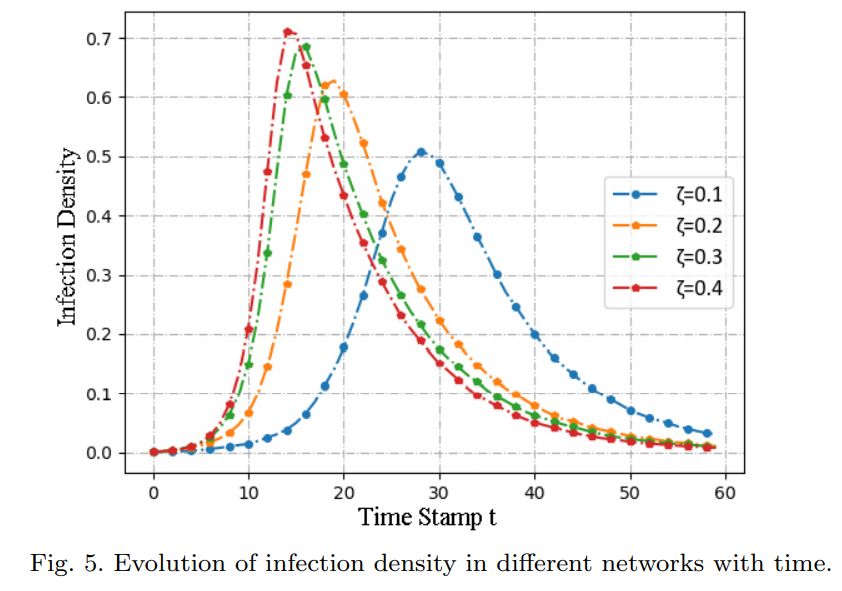
- With the random reconnection rate higher, the infection speed faster at the same time, the infection density higher in the network
③Simulation and Analysis of Source Node number
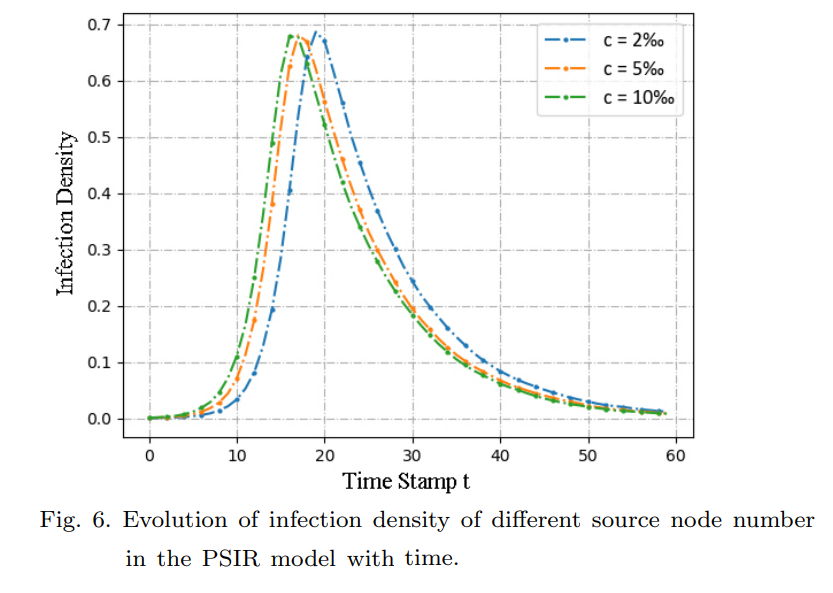
- The simulation shows that with the increase of the number of source nodes, the speed of behavior propagation would increase.
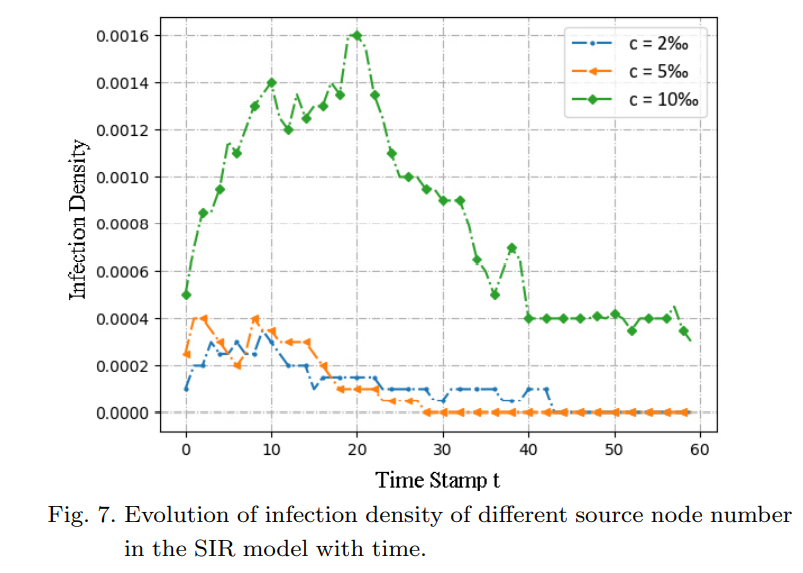
- The results show that pressure has a significant driving effect on behavior propagation.
④Simulation and Analysis of The Relative Location of Source Nodes

- The relative location of the source node is is divided into the crowded and the diffuse.
- The source nodes in the crowded state has a faster propagation speed than the diffuse state.
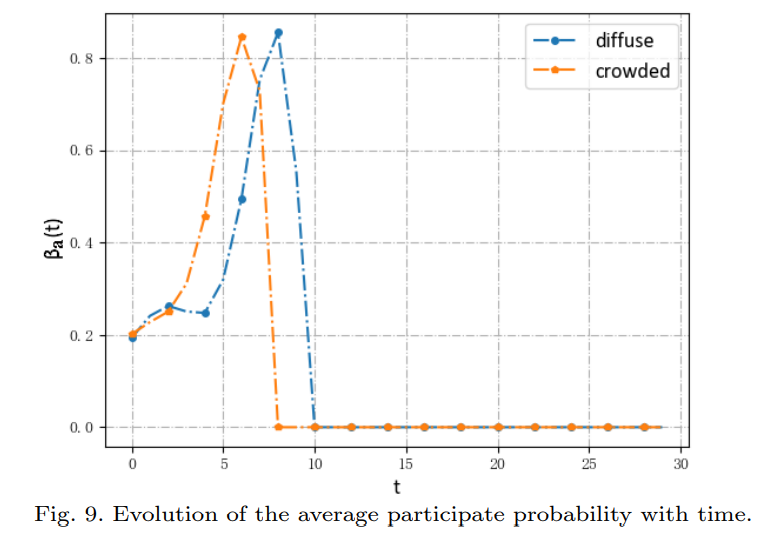
- The average participate probability means that the average value of the participate probability of all S nodes would become I nodes at time stamp t.
⑤Simulation and Analysis of Competition for Multiple Behavior
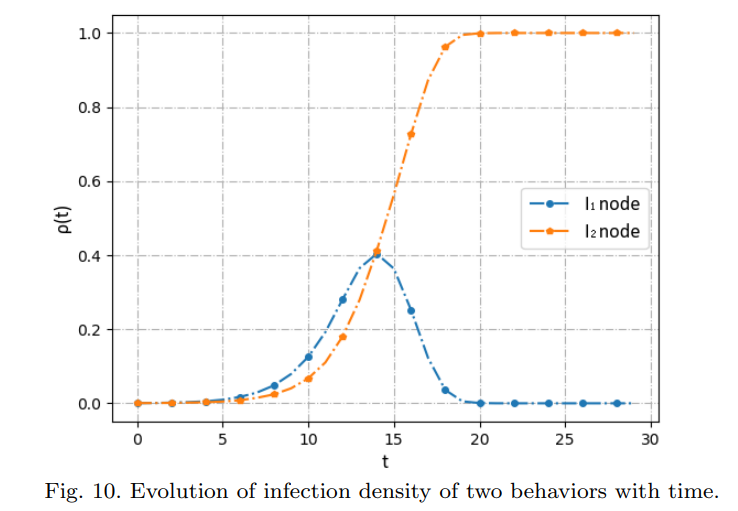
- There is the infection density curve of two behaviors I1 and I2 with time in the network.
- The two behaviors would compete with each other, one of two behaviors would win the competition and propagate widely in society, the other behavior would fade away.
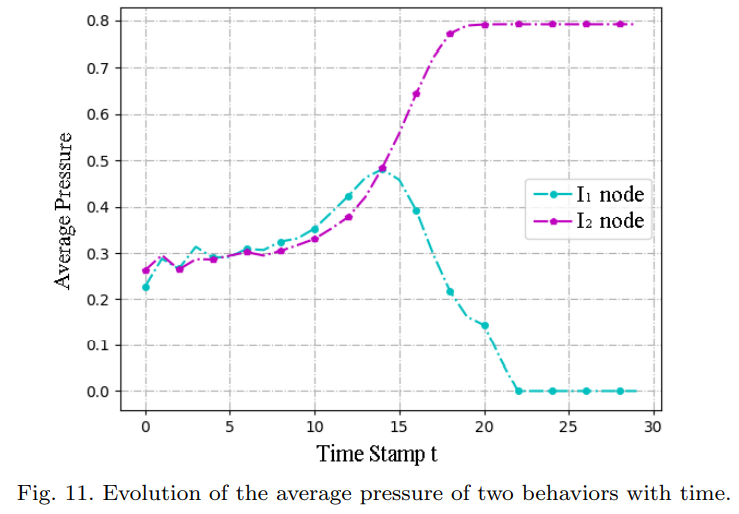
- The average pressure is caused by total I1 nodes or I2 nodes in networks.
- The two behaviors are constantly competing, when majority S nodes are infected, these two behaviors break the balance of competition,and the two behaviors no longer have the same pressure in the network.
Conclusion:
Summary of the above experimental results...
可以看出,本文重点在建立一个新的压力模型和机制,实验运用的是控制变量法,对模拟结果进行分析,图片处理较为小清新,但文中没有真实数据的比对,可能缺乏一点点说服力,总之,还是有所收获,为第一篇SIC继续努力!