三、查找与排序(下)
1、分治法(Divide and Conquer)
分解(divide):将原问题分解成一系列子问题
解决(conquer):递归地解决各子问题。若子问题足够小,则直接有解
合并(combine):将子问题的结果合并成原问题的解
优点:容易确定运行时间,提升一定效率(类比想象二分法)
2、快速排序算法
图解一下:
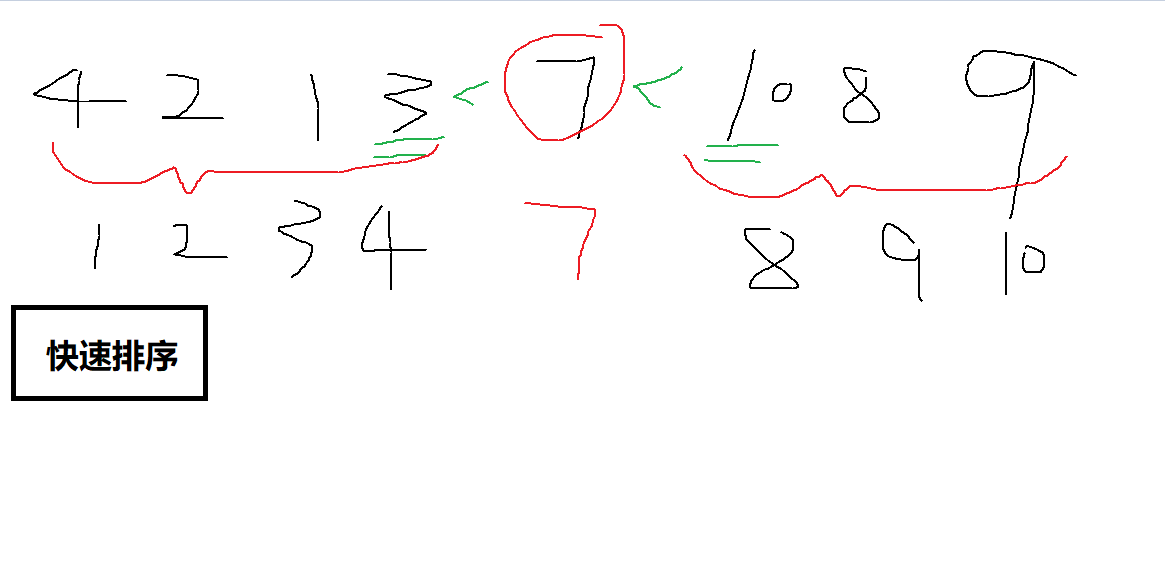
QuickSort(A,p,r)
if p<r
q = Partition(A,p,r)
QuickSort(A,p,q-1)
QuickSort(A,q+1,r)
//A[q]为大小居中的数
//找一个中间的数,其左边元素小于它,右边元素大于它;划分左边区域进行排序,右边区域进行排序;得出最终结果
3、一遍单向扫描法
图解一下:
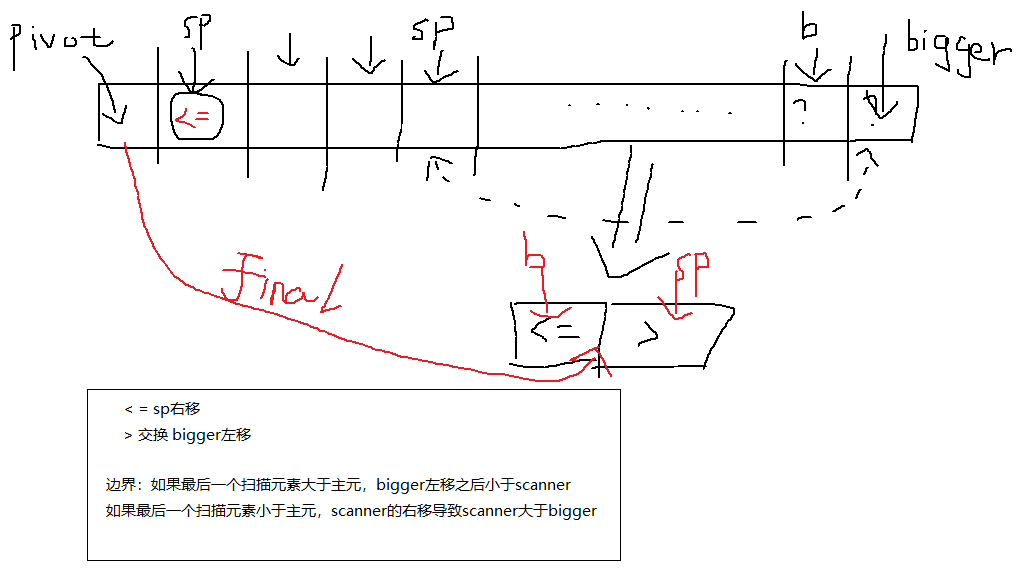
QuickSort
quickSort(A,p,r)
if(p<r)
q = partition(A,p,r)
quickSort(A,p,q-1)
qucikSort(A,q+1,r)
partition(A,p,r)
pivot = A[p]
sp = p+1 //扫描指针
bigger = r //右侧指针
while(sp<=bigger):
if(A[sp]<=pivot) //扫描元素小于主元
sp++
else
swap(A,sp,bigger) //扫描元素大于主元,二指针的元素交换,右指针左移
bigger--
swap(A,p,bigger)
return bigger
4、双向扫描法
头指针往中间扫描,从左找到大于主元的元素,从右边找到小于等于主元的元素二者交换,继续扫描,直到左侧无大元素,右侧无小元素
图解一下:
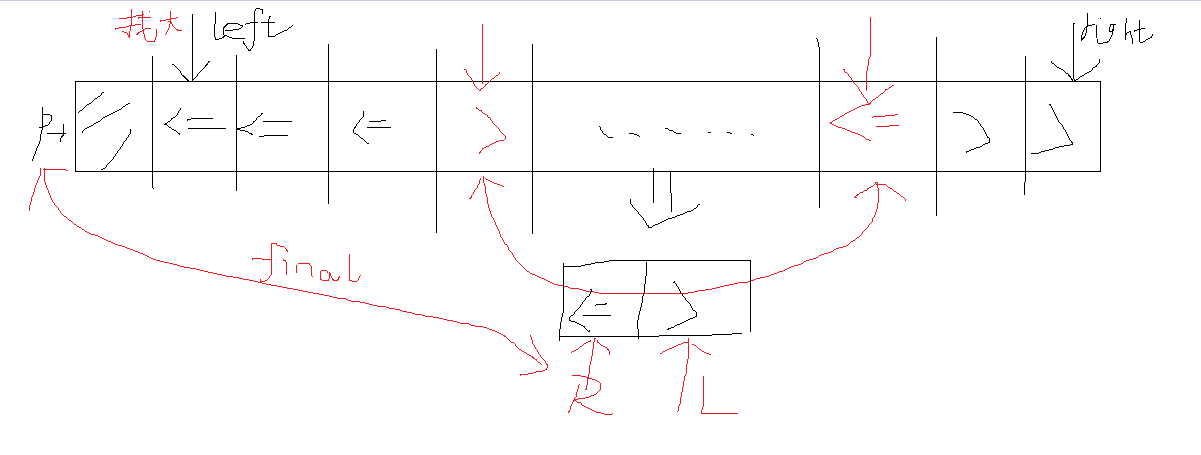
partiotion2(A,p,r) {
pivot = A[p];
left = p+1;
right = r;
while(left<=right) {
//left不停往右走,直到遇到大于主元的元素
while(left<=right&&A[left]<=pivot) left++;
//循环退出时,left一定指向第一个大于主元的位置
while(left<=right&&A[right]>pivot) right--;
//循环退出时,right一定指向最后一个小于等于主元的位置
if(left<right):
swap(A,left,right);
}
//while退出时,两者交错,且right指向的是最后一个小于等于主元的位置,也就是主元应该在的位置
swap(A,p,right);
return right;
}
5、有相同元素值的快排——三分法
图解了解:
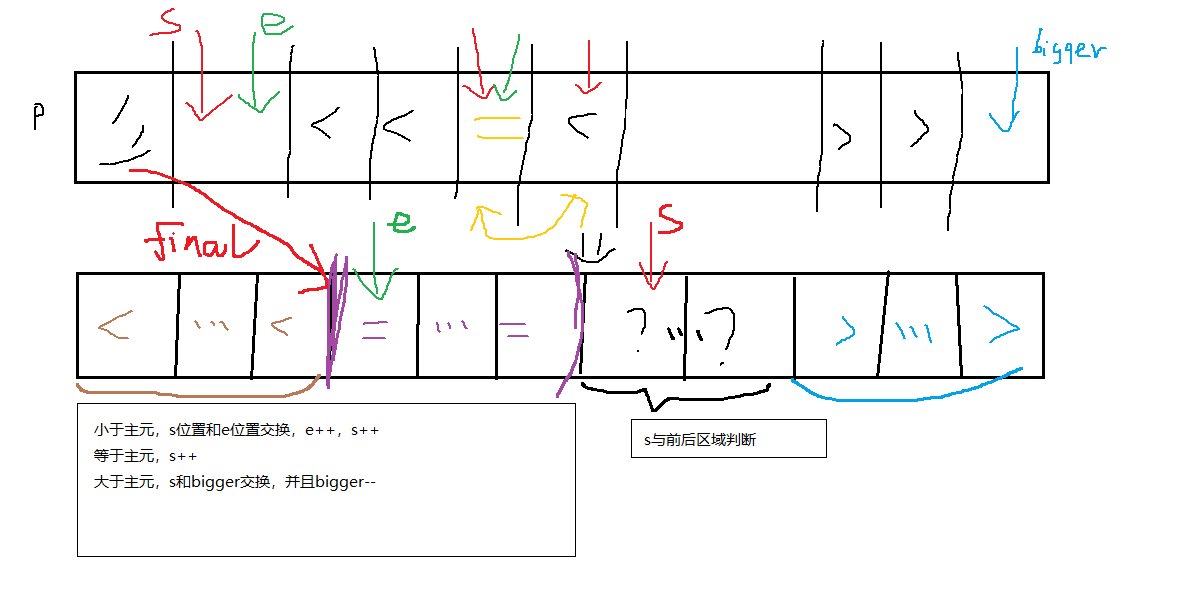
6、快速排序的三种优化
三点中值法:
思路:将主元尽可能的放在中间,优化时间复杂度由O(n^2)--->O(nlgn)
优化代码:
//在p,r,min之间,选一个中间值作为主元
int midIndex = p+((r-p)>>1); //中间下标
int midValueIndex = -1; //中值下标
if(A[p]<=A[midIndex]&&A[p]>=A[r]){
midValueIndex = p;
}else if(A[r]<=A[midIndex]&&A[r]>=A[p]){
midValueIndex = r;
}else {
midValueIndex = midIndex;
}
swap(A,p,midValueIndex);
绝对中值法:
思路:获取绝对的中值数,优化时间复杂度到O(n)
优化代码:
//获取绝对中间值
getMedian(arr,p,r){
size = r-p+1; //数组长度
//每5个元素一组
groupSize = (size%5==0)?(size/5):(size/5+1);
//存储各小组中值
medians[] = new [groupSize];
indexOfMedian = 0;
//对每一组进行插入排序
for(j=0;j<groupSize;j++){
//单独处理最后一组,因为可能不满5个元素
if(j=groupSize-1){
InsertSort(arr,p+j*5,r); //排序最后一组
medians[indexOfMedian++] = arr[(p+j*5+r)/2]; //最后一组的中间那个
}else {
InsertSort(arr,p+j*5,p+j*5+4); //排序非最后一组的某个组
medians[indexOfMedian++] = arr[p+j*5+2]; //当前组(排序后)的中间那个
}
}
//对medians排序
InsertSort(medians,0,medians.length-1);
return medians[medians.length/2];
}
若排序列表较短,直接插入排序:
具体原因:n(n-1)/2 < n(lgn+1) ,当n<8时,上式成立。
7、归并排序(Merge Sort)
-分解:将n个元素分成各含n/2个元素的子序列
-解决:将两个子序列递归的排序
-合并:合并两个已排序的子序列得到排序结果 【重点】
思路:一分为二,开辟一个新的辅助空间,优化时间复杂度到O(n)
图解一下:
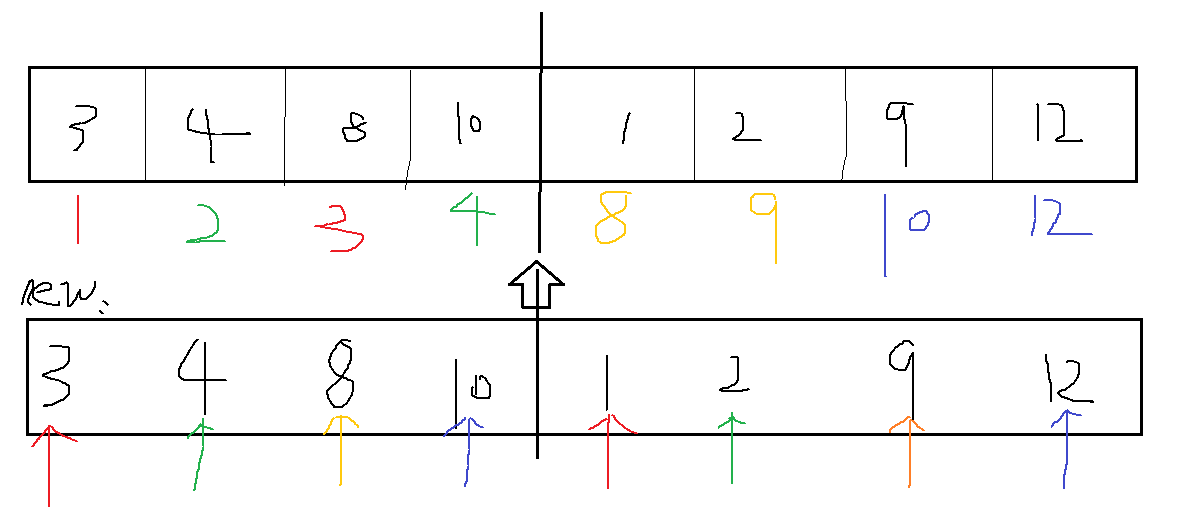
实现代码:
MergeSort
mergeSort(A,p,r){
if (p<r) {
mid = p+((r-p)>>1);
mergeSort(A,p,mid);
mergeSort(A,mid+1,r);
merge(A,p,mid,r);
}
}
helper = [A.length]; //开辟的新空间
merge(A,p,mid,r){
//先把A中的数据拷贝到helper中
copy(A,p,helper,p,r-p+1);
left = p; //左侧队伍的头指针,指向待比较元素
right = mid+1; //右侧队伍的头指针,指向待比较元素
current = p; //元素组的指针,指向待填入数据的位置
while(left<mid&&right<=r){
if(helper[left]<=helper[right]){
A[current] = helper[left];
current++;
left++;
}
}
while(left<=mid){
A[current] = helper[left];
current++;
left++;
}
}
8、最快效率求出乱序数组中第k小的数
题目描述:以尽高的效率求出一个乱序数组中按数值顺序的第k个元素值。期望达O(n),最差O(n^2)
图解一下:
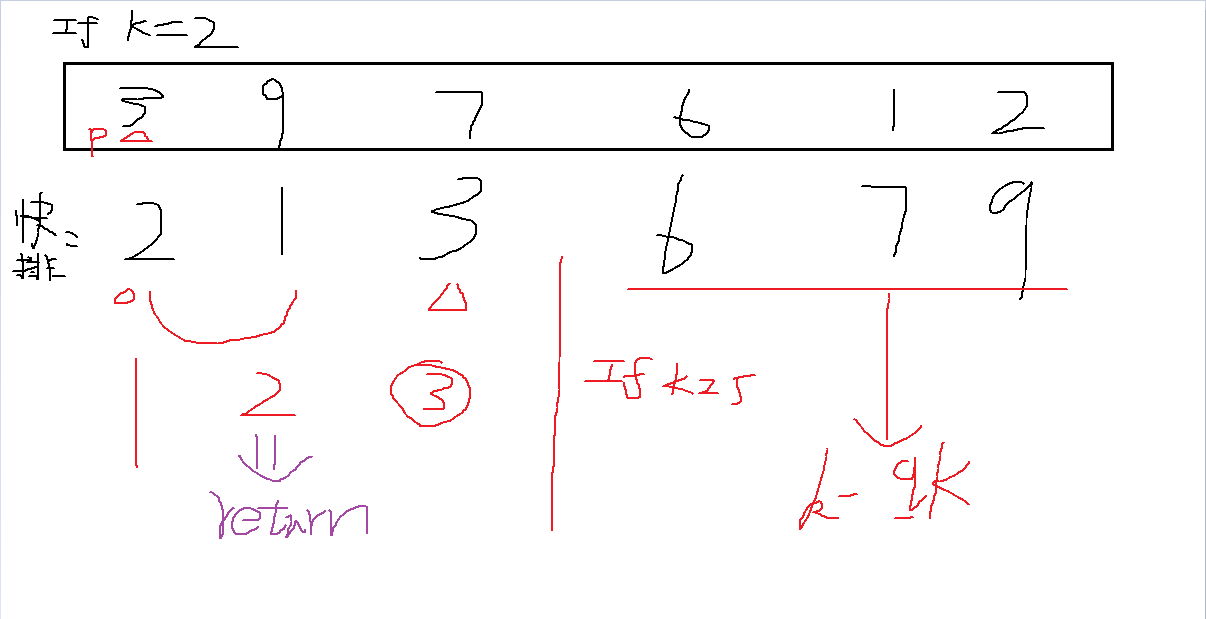
代码实现:
seclectK(A,p,r,k){
q = partition(A,p,r); //主元的下标
qK = q-p+1; //主元是第几个元素
if(qK == k) returnA[q];
else if (qk>k) return seclectK(A,p,q-1,k);
else return seclectK(A,q+1,r,k-qK);
}
partition2(A,p,r); //双向扫描
9、趣味题:寻找发帖水王
坊间风闻“水王”发帖数目超过帖子总数的一半,如果你有一个当前论坛上所有帖子的列表,其中帖子作者的ID也在表中,你能快速找出这个传说中的水王吗?
思路:
最原始的思路便是对所有的ID进行排序,统计ID出现的次数,若某个ID超过总数的一半则输出这个ID,时间复杂度为O(nlgn); 改进:如果每次删除2个不同的ID(无论是否包含水王的ID),那么剩下的ID中,水王的ID仍然是超过总数的一半,此时时间复杂度优化到O(n)
原始代码实现:
//缺点:要将整个数组进行重新排序
Arrays.sort(arr);
System.out.println(arr[arr.length/2]);
改进代码实现:
//侯选数,先定位第一个元素
candidate = arr[0];
//出现的次数
nTimes = 1;
//扫描数组
for(i=1;i<arr.length;i++){
//两两消减为0,把现在的元素作为候选值
if(nTimes==0){
candidate = arr[i];
nTimes = 1;
continue;
}
//遇到和候选值相同的,次数加一
if(arr[i]=candidate){
nTimes++;
}else{
nTimes--;
}
return candidate;
}
10、逆序对
合并有序数组:给定两个排序后的数组A和B,其中A的末端有足够的缓冲空间容纳B,编写一个方法,将B合并入A并排序
类似归并排序,图解一下:

11、用数组表示一棵二叉树
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,并且结点的存储位置,就是数组的下标索引。
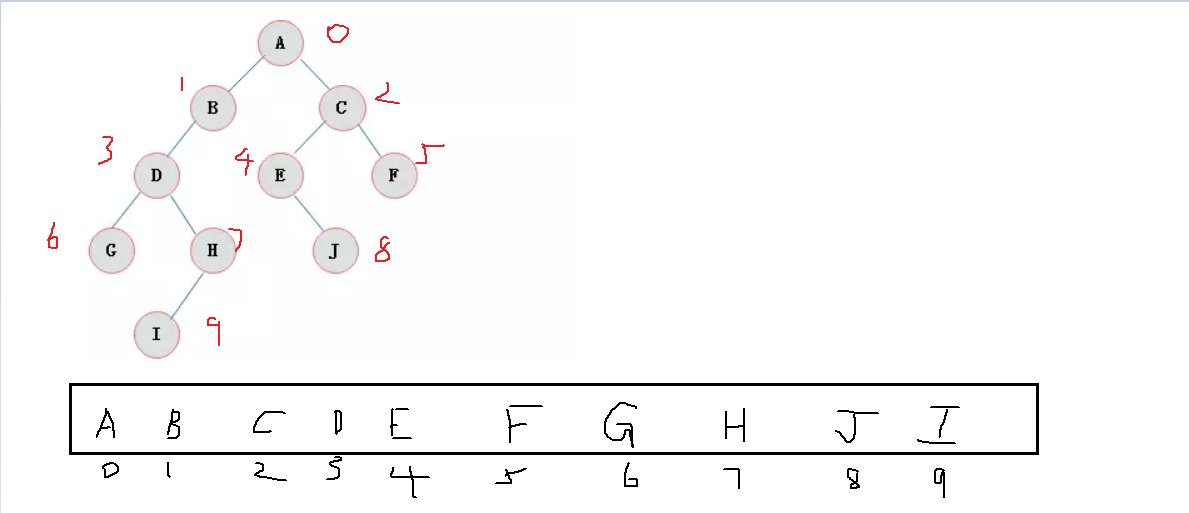
子节点:2i+1,2i+2 父节点:(i-1)/2
先序遍历(根左右):对访问到的每个结点*,先访问根结点,然后是左结点,然后是右结点
A,B,D,G,H,I,C,E,J,F
中序遍历(左根右) :对访问到的每个结点,先访问左结点,然后是根结点,然后是右结点
G,D,I,H,B,A,C,E,F,J
后序遍历(左右根):对访问到的每个结点,先访问左结点,然后是右结点,然后是根结点
G,I,H,D,J,E,F,B,C,A
public class TreeAndArray {
//先序遍历
private static void preOrder(int[] arr, int index){
if (index>=arr.length){
return;
}
System.out.println(arr[index]);//先输出根节点
preOrder(arr, index*2+1);//输出左子树
preOrder(arr,index*2+2);//输出右子树
}
//中序遍历
private static void inOrder(int[] arr,int index){
if (index>=arr.length){
return;
}
inOrder(arr, index*2+1);
System.out.println(arr[index]);
inOrder(arr,index*2+2);
}
//后序遍历
private static void postOder(int[] arr,int index){
if (index>=arr.length){
return;
}
postOder(arr, index*2+1);
postOder(arr,index*2+2);
System.out.println(arr[index]);
}
}
12、堆排序
二叉堆:近似完全二叉树 ,时间复杂度为O(nlogn) 并满足一下两个特性:
1.父节点的键值总是大于或等于(小于或等于)任何一个子节点的键值
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)
任意节点的值都大于其子节点的值——大顶堆
任意结点的值都小于其子节点的值——小顶堆
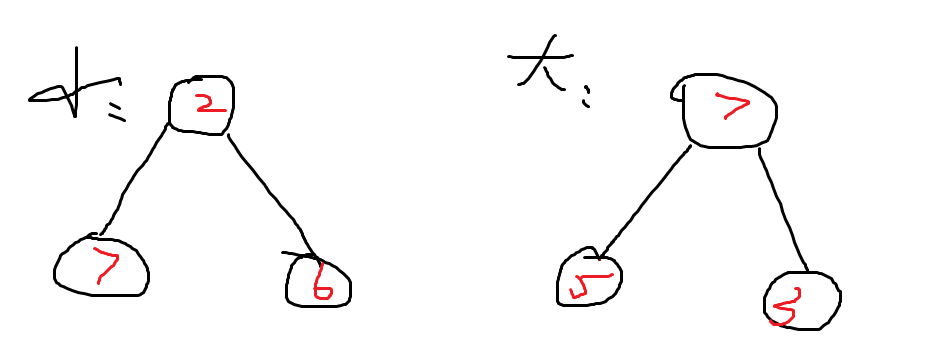
数组堆化:
MinHeap(A){
n = A.length;
for i from n/2-1 down to 0{
MinHeapFixDown(A,i);
}
}
MinHeapFixDown(A,i,n){
//找到左孩子
left = 2*i+1;
right = 2*i+2;
//左孩子已经越界,i就是叶子结点
(left>=n) {
return;
}
min = left;
if (right>=n) {
min = left;
}else{
if (A[right]<A[left]) {
min = right;
}
}
//min已经指向了左右孩子中较小的那个
//如果A[i]比两个孩子都小,则不需要调整
if (A[i]<=A[min]) {
return;
}
//否则,找到两个孩子中较小的,与i换位置
temp = A[i];
A[i] = A[min];
A[min] = temp;
//小孩子那个位置的值发生了变化,i变更为小孩子那个位置,递归调整
MinHeapFixDown(A,min,n);
}
sort(A){
//先对A进行堆化
MinHeap(A);
for (x=n-1;x>=0 ;x-- ) {
//把堆顶,0号元素和最后一个元素对调
swap(A,0,x);
//缩小堆的范围,对堆顶元素进行向下调整
MinHeapFixDown(A,0,x-1)
}
}
13、计数排序
图解了解:
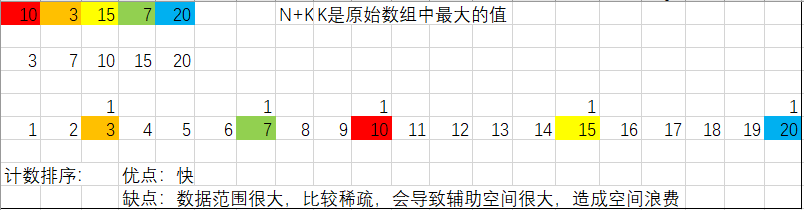
实现代码:
CountSort{ //[] source
[] helper = maxOf(source)+1; //maxOf求出source数组最大值
for(e : source) {
helper[e]++;
}
current = 0;
for(i=1; i<helper.length; i++){
while(helper[i]>0) {
source[current++] = i;
helper[i]--;
}
}
}
分析:
计数排序可以说是最快的排序算法,但是建议数据较为密集或范围较小的时候使用
14、桶排序(Bucket Sort)
图解事例:

有 11 个桶,编号从 0~10。每出现一个数,就将对应编号的桶中的放一个小旗子,最后只要数数每个桶中有几个小旗子就 OK 了。例如 2 号桶中有 1 个小旗子,表示 2 出现了一次;3 号桶中有 1 个小旗子,表示 3 出现了一次;5 号桶中有 2 个小旗子,表示 5 出现了两次;8 号桶中有 1 个小旗子,表示 8 出现了一次。
时间复杂度在O(N)~O(NlgN)
15、基数排序
图解一下:
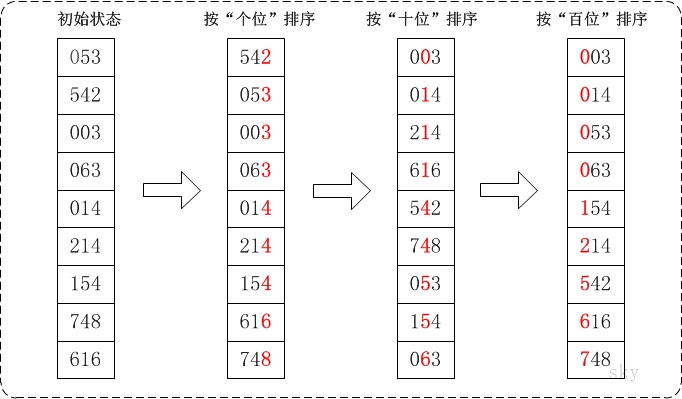
统一位数长度,接着从最低位开始,依次进行排序。时间复杂对O(KN) (K为最高位的次数 如:百-3) ,通常运用于10进制正数的排序。
/**
* 基数排序
* 考虑负数的情况还可以参考: https://code.i-harness.com/zh-CN/q/e98fa9
*/
public class RadixSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxDigit = getMaxDigit(arr);
return radixSort(arr, maxDigit);
}
/**
* 获取最高位数
*/
private int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private int[] radixSort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}
16、十种排序算法总结
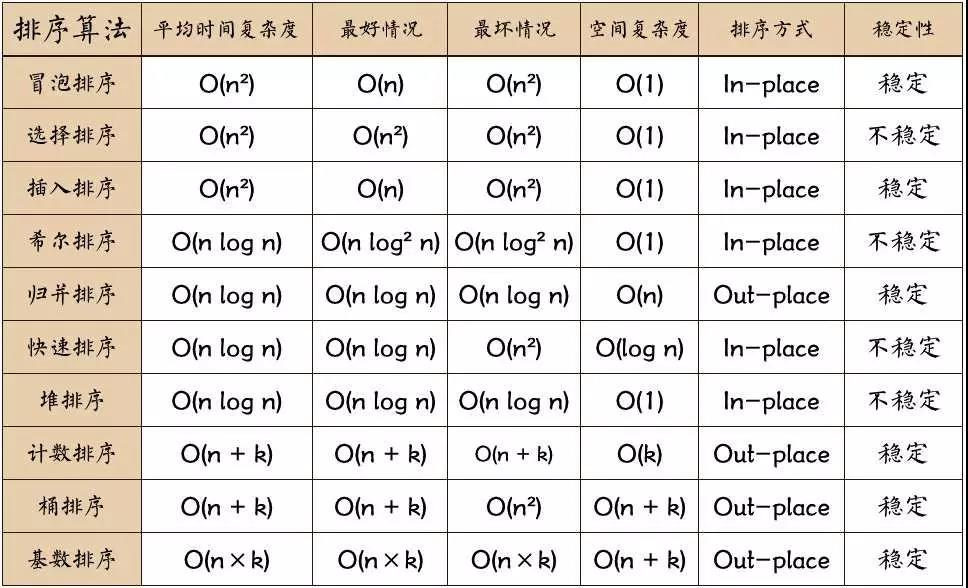
17、排序数组中找和的因子
给定已排序的数组arr和k,不重复打印arr中所有相加和为k的不降序的二元组
如: arr = {-8,-4,-3,0,2,4,5,8,9,10} k=10
输出:(0,10)(2,8)
思路:
注意条件已排序的数组,所以我们采用二分查找中的双向扫描法,两个指针往中间扫,输出和为k的值。 这里判断不重复,使得left下标值不相同即可,因为k值是定的,left不同,right也不同了
代码:
private static void printTwoPair(int[] arr, int k) {
//边界条件判断
if (arr == null || arr.length < 2) {
return;
}
int left = 0;
int right = arr.length - 1;
int sum = 0
while (left < right) {
sum = arr[left]+arr[right];
if(sum<k){
++left;
}
else if(sum>k){
--right;
}
else{
if (left == 0 || arr[left -1] != arr[left]){ //判断不重复
System.out.print(arr[left] + "," +arr[right] + "
");
}
++left;
--right;
}
}
}
18、topK
求海量数据(正整数)按逆序排列的前k个数(topK),因为数据量太大,不能全部存储在内存中,只能一个一个地从磁盘或者网络上读取数据,请设计一个高效的算法来解决这个问题。
第一行:用户输入K,代表要求得topK随后的N(不限制)行,每一行是一个整数代表用户输入的数据
用户输入-1代表输入终止
请输出topK,从小到大,空格分割
实际运用场景:比如从1千万搜索记录中找出最热门的10个关键词
import java.util.Arrays;
import java.util.Scanner;
public class TopK {
static int[] heap;
static int index = 0;
static int k;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
k = sc.nextInt();
heap = new int[k];
int x = sc.nextInt();
while (x != -1) {
deal(x);//处理x
x = sc.nextInt();
}
printRs();
}
private static void printRs() {
System.out.println(Arrays.toString(heap));
}
/**
* 如果数据数量小于等于k,直接加入堆中
* 等于k的时候,进行堆化
* @param x
*/
private static void deal(int x) {
if (index < k) {
heap[index++] = x;
if (index == k) {
//堆化
makeMinHeap(heap);
}
} else
//x和堆顶进行比较,如果x大于堆顶,x将堆顶挤掉并向下调整
if (heap[0] < x) {
heap[0] = x;
MinHeapFixDown(heap, 0, k);
printRs();
}
}
static void makeMinHeap(int[] A) {
int n = A.length;
for (int i = n / 2 - 1; i >= 0; i--) {
MinHeapFixDown(A, i, n);
}
}
static void MinHeapFixDown(int[] A, int i, int n) {
// 找到左右孩子
int left = 2 * i + 1;
int right = 2 * i + 2;
//左孩子已经越界,i就是叶子节点
if (left >= n) {
return;
}
int min = left;
if (right >= n) {
min = left;
} else {
if (A[right] < A[left]) {
min = right;
}
}
//min指向了左右孩子中较小的那个
// 如果A[i]比两个孩子都要小,不用调整
if (A[i] <= A[min]) {
return;
}
//否则,找到两个孩子中较小的,和i交换
int temp = A[i];
A[i] = A[min];
A[min] = temp;
//小孩子那个位置的值发生了变化,i变更为小孩子那个位置,递归调整
MinHeapFixDown(A, min, n);
}
}