• Educational Codeforces Round 71 (Rated for Div. 2)

    https://codeforces.com/contest/1207

    这次没打rating

    A、There Are Two Types Of Burgers

    数据规模不大，暴力即可

     1 #include<iostream>
 2 #include<sstream>
 3 #include<fstream>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<iomanip>
 7 #include<cstdlib>
 8 #include<cctype>
 9 #include<vector>
10 #include<string>
11 #include<cmath>
12 #include<ctime>
13 #include<stack>
14 #include<queue>
15 #include<map>
16 #include<set>
17 #define mem(a,b) memset(a,b,sizeof(a))
18 #define random(a,b) (rand()%(b-a+1)+a)
19 #define ll long long
20 #define ull unsigned long long
21 #define e 2.71828182
22 #define Pi acos(-1.0)
23 #define ls(rt) (rt<<1)
24 #define rs(rt) (rt<<1|1)
25 #define lowbit(x) (x&(-x))
26 using namespace std;
27 int read()
28 {
29     int s=1,x=0;
30     char ch=getchar();
31     while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
32     while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
33     return x*s;
34 }
35 int b,p,f,h,c;
36 void solve()
37 {
38     int res=-1;
39     for(int i=0;i<=min(p,b>>1);++i)
40     {
41         int j=min(f,(b-i*2)>>1);
42         res=max(res,h*i+c*j);
43     }
44     cout<<res<<endl;
45 }
46 int main()
47 {
48     int test=read();
49     while(test--)
50     {
51         b=read(),p=read(),f=read(),h=read(),c=read();
52         solve();
53     }
54 }
    View Code

    B、Square Filling

     给定一个01矩阵a，全0矩阵b，每次操作能将2*2的元素变为1，求操作序列使得矩阵b变为a，若不能则输出-1

    刚好在做DLX的习题，想到转化为用DLX解重复覆盖问题。

      1 #include<iostream>
  2 #include<sstream>
  3 #include<fstream>
  4 #include<algorithm>
  5 #include<cstring>
  6 #include<iomanip>
  7 #include<cstdlib>
  8 #include<cctype>
  9 #include<vector>
 10 #include<string>
 11 #include<cmath>
 12 #include<ctime>
 13 #include<stack>
 14 #include<queue>
 15 #include<map>
 16 #include<set>
 17 #define mem(a,b) memset(a,b,sizeof(a))
 18 #define random(a,b) (rand()%(b-a+1)+a)
 19 #define ll long long
 20 #define ull unsigned long long
 21 #define e 2.71828182
 22 #define Pi acos(-1.0)
 23 #define ls(rt) (rt<<1)
 24 #define rs(rt) (rt<<1|1)
 25 #define lowbit(x) (x&(-x))
 26 using namespace std;
 27 const int MAXN=2555;
 28 const int MAXM=2555;
 29 const int MAX=7e6+5;
 30 const int INF=0x3f3f3f3f;
 31 int read()
 32 {
 33     int s=1,x=0;
 34     char ch=getchar();
 35     while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
 36     while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
 37     return x*s;
 38 }
 39 int N,M;
 40 struct DLX
 41 {
 42     int n,m,cnt,ansd;
 43     int U[MAX],D[MAX],R[MAX],L[MAX],row[MAX],col[MAX];
 44     int H[MAXN],S[MAXM],ans[MAXN],tmp[MAXN];
 45     bool v[MAX];
 46     void init(int _n,int _m)
 47     {
 48         n=_n,m=_m,ansd=INF;
 49         for(int i=0;i<=m;++i)
 50         S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
 51         R[m]=0,L[0]=m,cnt=m;
 52         mem(H,-1);
 53     }
 54     void add(int r,int c)
 55     {
 56         ++S[col[++cnt]=c];
 57         row[cnt]=r;
 58         D[cnt]=D[c],U[D[c]]=cnt;
 59         U[cnt]=c,D[c]=cnt;
 60         if(H[r]<0) H[r]=L[cnt]=R[cnt]=cnt;
 61         else R[cnt]=R[H[r]],L[R[H[r]]]=cnt,L[cnt]=H[r],R[H[r]]=cnt;
 62     }
 63     void remove(int c)
 64     {
 65         for(int i=D[c];i!=c;i=D[i])
 66         L[R[i]]=L[i],R[L[i]]=R[i];
 67     }
 68     void resume(int c)
 69     {
 70         for(int i=U[c];i!=c;i=U[i])
 71         L[R[i]]=R[L[i]]=i;
 72     }
 73     int h()
 74     {
 75         int ret=0;
 76         for(int i=R[0];i!=0;i=R[i]) v[i]=true;
 77         for(int i=R[0];i!=0;i=R[i])
 78         {
 79             if(!v[i]) continue;
 80             ret++,v[i]=false;
 81             for(int j=D[i];j!=i;j=D[j])
 82             for(int k=R[j];k!=j;k=R[k])
 83             v[col[k]]=false;
 84         }    
 85         return ret;
 86     } 
 87     bool dance(int d)
 88     {
 89         //if(d+h()>=ansd) return;
 90         if(R[0]==0)
 91         {
 92             if(d<ansd) 
 93             {
 94                 ansd=d;
 95                 for(int i=0;i<d;++i) ans[i]=tmp[i];
 96             }
 97             return true;
 98         }
 99         int c=R[0];
100         for(int i=R[0];i!=0;i=R[i])
101         if(S[i]<S[c]) c=i;
102         for(int i=D[c];i!=c;i=D[i])
103         {
104             remove(i);
105             for(int j=R[i];j!=i;j=R[j]) remove(j);
106             tmp[d]=row[i];
107             if(dance(d+1)) return true;
108             for(int j=L[i];j!=i;j=L[j]) resume(j);
109             resume(i);
110         }
111         return false;
112     }
113 }dlx;
114 int G[51][51];
115 int pos[51][51];
116 struct node
117 {
118     int x,y;
119 }data[MAXN];
120 int main()
121 {
122     N=read(),M=read();
123     int cnt=0;
124     for(int i=1;i<=N;++i)
125     for(int j=1;j<=M;++j)
126     {
127         G[i][j]=read();
128         if(G[i][j]) pos[i][j]=++cnt;
129     }
130     dlx.init(N*M,cnt);
131     cnt=0;
132     for(int i=1;i<=N-1;++i)
133     for(int j=1;j<=M-1;++j)
134     {
135         bool flag=true;
136         for(int x=1;x<=2&&flag;++x)
137         for(int y=1;y<=2&&flag;++y)
138         if(!G[i+x-1][j+y-1]) flag=false;
139         
140         if(flag)
141         {
142             dlx.add(++cnt,pos[i][j]);
143             dlx.add(cnt,pos[i][j+1]);
144             dlx.add(cnt,pos[i+1][j]);
145             dlx.add(cnt,pos[i+1][j+1]);
146             data[cnt].x=i,data[cnt].y=j;
147         }
148         
149     }
150     
151     dlx.dance(0);
152     if(dlx.ansd==INF) return 0*printf("%d",-1);
153     cout<<dlx.ansd<<endl;
154     for(int i=0;i<dlx.ansd;++i) 
155     {
156         int r=dlx.ans[i];
157         cout<<data[r].x<<' '<<data[r].y<<endl;
158     }
159     
160 }
    View Code

    其实只要模拟就行了，只有当矩阵a有2*2的元素全1时才在矩阵b对应位置改，比较最后的矩阵a和矩阵b，贴下大佬代码

     1 #include <bits/stdc++.h>
 2 using namespace std;
 3 #define ll long long
 4 #define pb push_back
 5 #define mp make_pair
 6 const int N=100;
 7 int a[N][N],b[N][N];
 8 int main()
 9 {
10     int n,m;
11     scanf("%i %i",&n,&m);
12     for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%i",&a[i][j]);
13     vector<pair<int,int>> ans;
14     for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
15     {
16         if(a[i][j]==1 && a[i+1][j]==1 && a[i][j+1]==1 && a[i+1][j+1]==1)
17         {
18             b[i][j]=b[i+1][j]=b[i][j+1]=b[i+1][j+1]=1;
19             ans.pb({i,j});
20         }
21     }
22     for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(a[i][j]!=b[i][j]) return 0*printf("-1
");
23     printf("%i
",ans.size());
24     for(auto p:ans) printf("%i %i
",p.first,p.second);
25     return 0;
26 }
    View Code

    C、Gas Pipeline

    给定一个长为n的01串，emm，看图吧

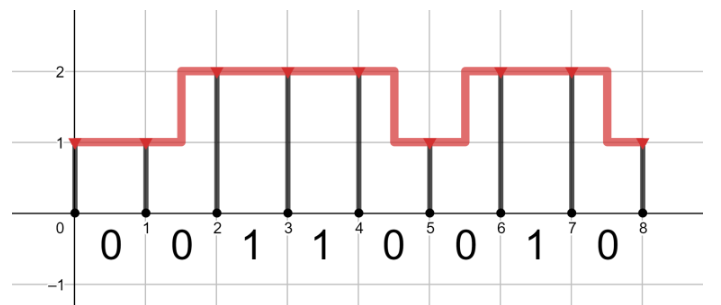
    令str表示01串，则str[i]=1表示第i个区间高度必须为2，str[i]=0表示第i个区间高度可以不必为2。（i>=1）

    用dp[i][1]表示第i个区间后半段高度为1时的最小花费，dp[i][2]表示第i个区间后半段高度为2时的最小花费。

    题目中给定第1个区间左端柱子高度和第n个区间右端柱子高度是1，因此初始化dp[0][1]=b，dp[0][2]=INF，最后的结果即是dp[n][1]。

    递推式列出情况推一推就好：

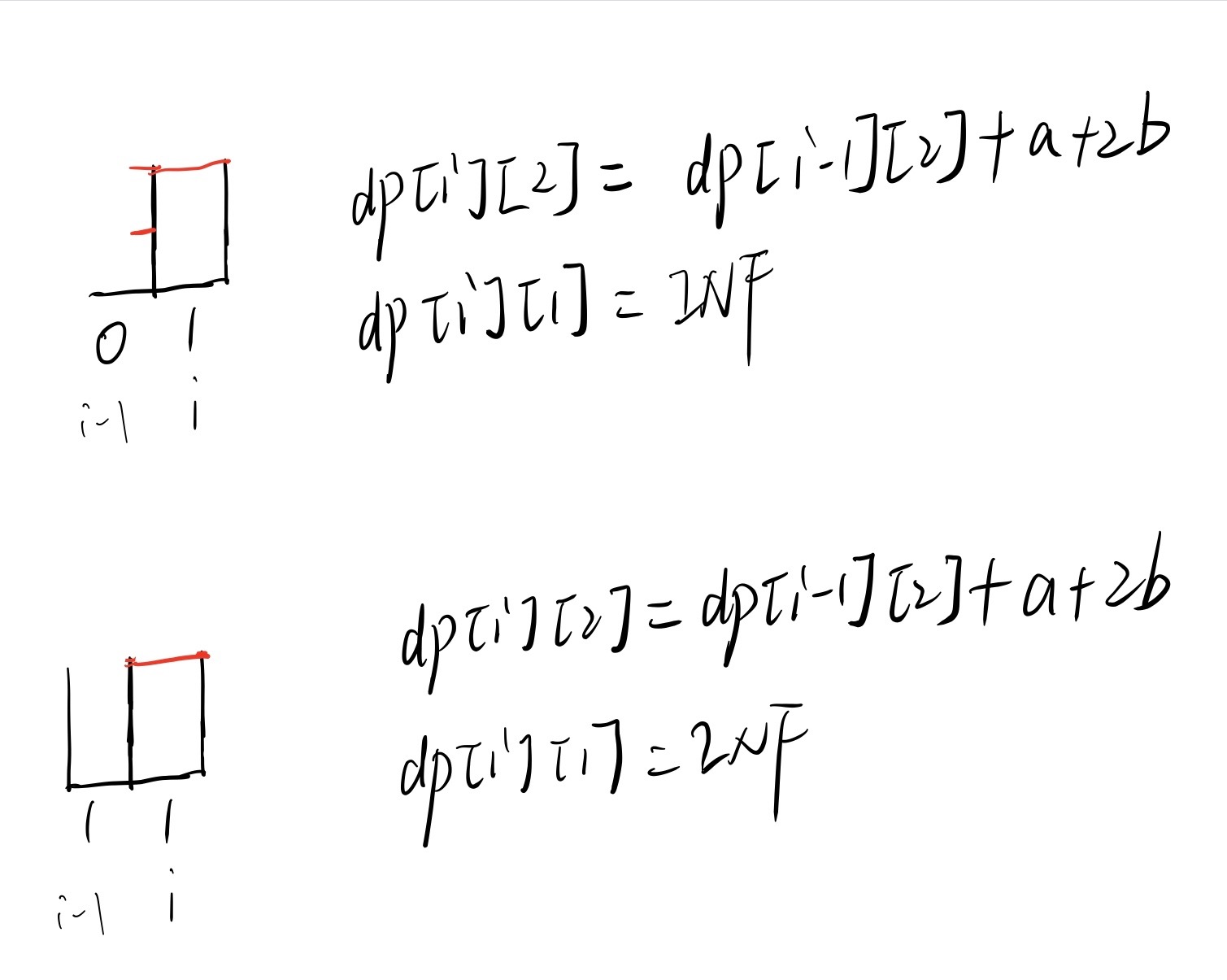
     1 #include<iostream>
 2 #include<sstream>
 3 #include<fstream>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<iomanip>
 7 #include<cstdlib>
 8 #include<cctype>
 9 #include<vector>
10 #include<string>
11 #include<cmath>
12 #include<ctime>
13 #include<stack>
14 #include<queue>
15 #include<map>
16 #include<set>
17 #define mem(a,b) memset(a,b,sizeof(a))
18 #define random(a,b) (rand()%(b-a+1)+a)
19 #define ll long long
20 #define ull unsigned long long
21 #define e 2.71828182
22 #define Pi acos(-1.0)
23 #define ls(rt) (rt<<1)
24 #define rs(rt) (rt<<1|1)
25 #define lowbit(x) (x&(-x))
26 using namespace std;
27 const int MAXN=2e5+5;
28 const ll INF=1ll<<62;
29 char str[MAXN];
30 ll dp[MAXN][3];
31 ll read()
32 {
33     ll s=1,x=0;
34     char ch=getchar();
35     while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
36     while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
37     return x*s;
38 }
39 int main()
40 {
41     ll test=read();
42     while(test--)
43     {
44         ll n=read(),a=read(),b=read();
45         scanf("%s",str+1);    
46         dp[0][1]=b,dp[0][2]=INF,str[0]='0';
47         for(int i=1;i<=n;++i)
48         {
49             if(str[i]=='1')
50             {
51                 dp[i][1]=INF;            
52                 dp[i][2]=dp[i-1][2]+a+2*b;
53             }
54             else if(str[i]=='0')
55             {
56                 if(str[i-1]=='0')
57                 {   
58                     dp[i][1]=min(dp[i-1][1]+a+b,dp[i-1][2]+2*a+b);
59                     dp[i][2]=min(dp[i-1][1]+2*a+2*b,dp[i-1][2]+a+2*b);
60                 }
61                 else
62                 {
63                     dp[i][1]=dp[i-1][2]+2*a+b;
64                     dp[i][2]=dp[i-1][2]+a+2*b;
65                 }
66             }
67         }
68         /*for(int i=1;i<=n;++i)
69         cout<<dp[i][1]<<' ';cout<<endl;
70         for(int i=1;i<=n;++i)
71         cout<<dp[i][2]<<' ';cout<<endl;*/
72         cout<<dp[n][1]<<endl;
73     } 
74 }
    View Code

    D、Number Of Permutations

    定义一个pair序列为bad：pair的first元素为非降，或second元素为非降

    给定一个pair序列，求使得该序列为good（非bad）的排列数，模998244353

    正难则反

    容斥原理

    记一个RE的bug:

     1 #include<iostream>
 2 #include<sstream>
 3 #include<fstream>
 4 #include<algorithm>
 5 #include<cstring>
 6 #include<iomanip>
 7 #include<cstdlib>
 8 #include<cctype>
 9 #include<vector>
10 #include<string>
11 #include<cmath>
12 #include<ctime>
13 #include<stack>
14 #include<queue>
15 #include<map>
16 #include<set>
17 #define mem(a,b) memset(a,b,sizeof(a))
18 #define random(a,b) (rand()%(b-a+1)+a)
19 #define ll long long
20 #define ull unsigned long long
21 #define e 2.71828182
22 #define Pi acos(-1.0)
23 #define ls(rt) (rt<<1)
24 #define rs(rt) (rt<<1|1)
25 #define P pair<int,int>
26 #define lowbit(x) (x&(-x))
27 using namespace std;
28 const int MAXN=1e6+5; 
29 const int MOD=998244353;
30 P seq[MAXN];
31 ll fac[MAXN];
32 int n;
33 int read()
34 {
35     int s=1,x=0;
36     char ch=getchar();
37     while(!isdigit(ch)) {if(ch=='-') s=-1;ch=getchar();}
38     while(isdigit(ch)) {x=10*x+ch-'0';ch=getchar();}
39     return x*s;
40 }
41 void init()
42 {
43     fac[0]=1;
44     for(int i=1;i<=n;++i)
45     fac[i]=fac[i-1]*i%MOD;
46 }
47 bool cmp(P a,P b)
48 {
49     return a.second<b.second;
50 }
51 int main()
52 {
53     n=read();
54     for(int i=1;i<=n;++i)
55     seq[i].first=read(),seq[i].second=read();
56     init();
57     //calculate cnt2
58     ll cnt2=1,tmp=1;
59     sort(seq+1,seq+n+1,cmp);
60     for(int i=2;i<=n;++i)
61     if(seq[i].second==seq[i-1].second) tmp++;
62     else cnt2=cnt2*fac[tmp]%MOD,tmp=1;
63     cnt2=cnt2*fac[tmp]%MOD;
64     
65     //calculate cnt1
66     ll cnt1=1;tmp=1;
67     sort(seq+1,seq+1+n);
68     for(int i=2;i<=n;++i)
69     if(seq[i].first==seq[i-1].first) tmp++;
70     else cnt1=cnt1*fac[tmp]%MOD,tmp=1;
71     cnt1=cnt1*fac[tmp]%MOD;
72         
73     //calculate cnt3
74     ll cnt12=1;tmp=1;
75     bool flag=true;
76     for(int i=2;i<=n&&flag;++i)
77     {
78         if(seq[i].second<seq[i-1].second) flag=false;
79         else if(seq[i].first==seq[i-1].first&&
80                 seq[i].second==seq[i-1].second)
81             tmp++;
82         else cnt12=cnt12*fac[tmp]%MOD,tmp=1;
83     }
84     cnt12=cnt12*fac[tmp]%MOD;
85     if(!flag) cnt12=0;
86     
87     cout<<(fac[n]-cnt1-cnt2+cnt12+MOD*2)%MOD<<endl;
88     return 0;
89 }
    View Code
  • 相关阅读:
    Java 日期字符串与日期类型转换
    Android 开发笔记“关闭默认键盘”
    MySql 日期转字符串
    Android 开发笔记“调用.net webservice遇到的问题”
    远程连接MySQL 不允许
    未能启用约束。一行或多行中包含违反非空、唯一或外键约束的值。
    Android 开发笔记“浅谈DDMS视图”
    Android 开发笔记“Eclipse 调试和快捷键”
    Android 开发笔记“程序安装包APK的制作”
    第四周进度条
  • 原文地址：https://www.cnblogs.com/wangzhebufangqi/p/11402694.html
Copyright © 2020-2023  润新知