Leetcode 130. Surrounded Regions

Description: Given an m x n matrix board containing 'X' and 'O', capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Link: 130. Surrounded Regions

Examples:

Example 1:

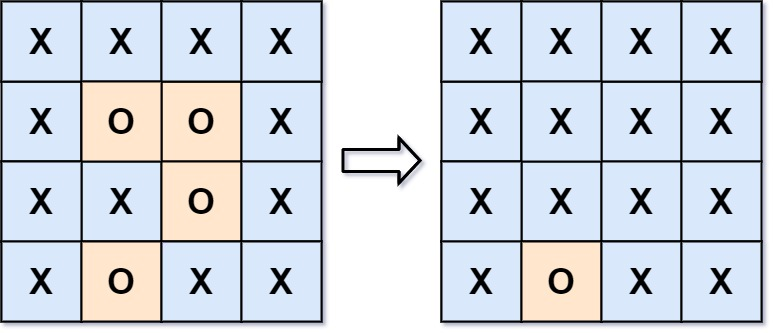
Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Example 2:
Input: board = [["X"]]
Output: [["X"]]

思路: 题目的意思是将被包围的O全部替换成X,那么什么算是被包围呢？O不在四条边上且不与在四条边上的“O"连接(水平或垂直连接)，这样的O要被替换。所以DFS找到所有在四条边上或与在四条边上的“O"连接的所有O,用其他字母标识，这些O没有被surrounded。DFS结束后，遍历所有的点，O --> X, A --> O

class Solution(object):
    def solve(self, board):
        """
        :type board: List[List[str]]
        :rtype: None Do not return anything, modify board in-place instead.
        """
        if len(board) == 0: return
        m = len(board)
        n = len(board[0])
        for i in range(m):
            for j in range(n):
                if (i == 0 or j == 0 or i == m-1 or j == n-1) and board[i][j] == 'O':
                    self.dfs(board, i, j)
        for i in range(m):
            for j in range(n):
                if board[i][j] == "O":
                    board[i][j] = "X"
                if board[i][j] == "A":
                    board[i][j] = "O"
        
    def dfs(self, board, i, j):
        dirs = [(0, 1), (0, -1), (1, 0), (-1,0)]
        m = len(board)
        n = len(board[0])
        board[i][j] = "A"
        for d in dirs:
            x = i + d[0]
            y = j + d[1]
            if x>=0 and x <m and y >=0 and y < n and board[x][y] == "O":
                self.dfs(board, x, y)

PS: 二叉树有连个遍历的方向：左右，矩阵有四个遍历的方向，二叉树遍历的结束条件是叶子节点，矩阵是边框的限制。

日期: 2021-03-25  最近心情好复杂啊