第一次作业
题目要求
第一次作业要求实现简单的多项式求导计算,且保证输入格式一定正确。
实现思路
使用Item类来作为“项”,其中包含coef(系数)和index(指数)两个属性,这两个属性可以确定一个“项”。然后我用Poly类来作为“多项式”,维护一个Item类型的集合,多项式即代表集合中所有项相加。还有一个Regex类用来将输入的字符串解析为一个Poly对象。最后是MainClass类,在其main方法中将输入、解析、求导、输出这一过程串联起来。
UML类图如下:
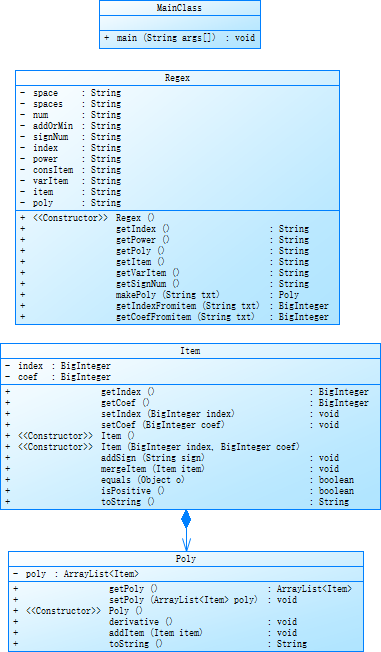
多项式的化简,只需要关注一些特定的点就可以:同类项合并,零不输出,乘1省略,第一项放正项等等。
代码度量分析
|
Type Name |
NOF |
NOPF |
NOM |
NOPM |
LOC |
WMC |
NC |
DIT |
LCOM |
FANIN |
FANOUT |
|
Item |
2 |
0 |
11 |
11 |
92 |
24 |
0 |
0 |
0.181818 |
0 |
0 |
|
MainClass |
0 |
0 |
1 |
1 |
17 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
Poly |
1 |
0 |
6 |
6 |
62 |
13 |
0 |
0 |
0 |
0 |
0 |
|
Regex |
11 |
0 |
10 |
10 |
128 |
18 |
0 |
0 |
0.4 |
0 |
0 |
Bug
第一次作业在强测中被找出bug,是正则表达式在匹配时产生了栈溢出。我是用一个正则表达式对整个式子进行匹配,其中用到了“*”使得匹配过程变得艰难。后来发现在我的正则表达式的逻辑中,完全可以将“*”变成“?”,能产生同样的效果,效率却大大提升,也不会再产生栈溢出错误。
找别人bug的时候,一开始我还不会用sympy,而是用java做了一个”测试房间”,用来产生数据---用此数据测试屋内所有人的代码---用自己写的Regex类将他们的输出解析为Poly对象---比对这些Poly对象有没有和自己不同的。如果一个测试数据只有1-2人与自己不同,那么大概率是他们错了;如果所有人都和我不同,那就是我错了。
反思
在第一次作业中,我将空格出现的所有情况都写在了正则表达式里。后来从同学那里学到了预处理的方法,一开始去掉所有空格,把连续的+-号化为1个等等,觉得自己之前的办法太累赘了。后来预处理的方法用到了作业二中。
第二次作业
题目要求
第二次作业在第一次作业的基础上,加入了sin和cos,且不保证输入格式正确。
实现思路
正余弦的计算较为简单,只需要在原来Item类中加入sinIndex和cosIndex两个属性。检验格式也好办,因为不会出现因为空格而导致的WF,所以只需要先去掉所有空格,然后用一整串正则表达式来匹配;对于幂次的限制,只需要在解析字符串的过程中,发现幂次超值,抛出异常。难点在于表达式的化简,因为三角函数变换规则较为灵活,不像作业1有唯一确定的化简道路。
相比于作业1,新填加了Simplify类用来完成化简工作,SimplifyRule接口,以及SimplifyRule1和SimplifyRule2两个实现SimplifyRule接口的具体化简规则。UML类图如下:
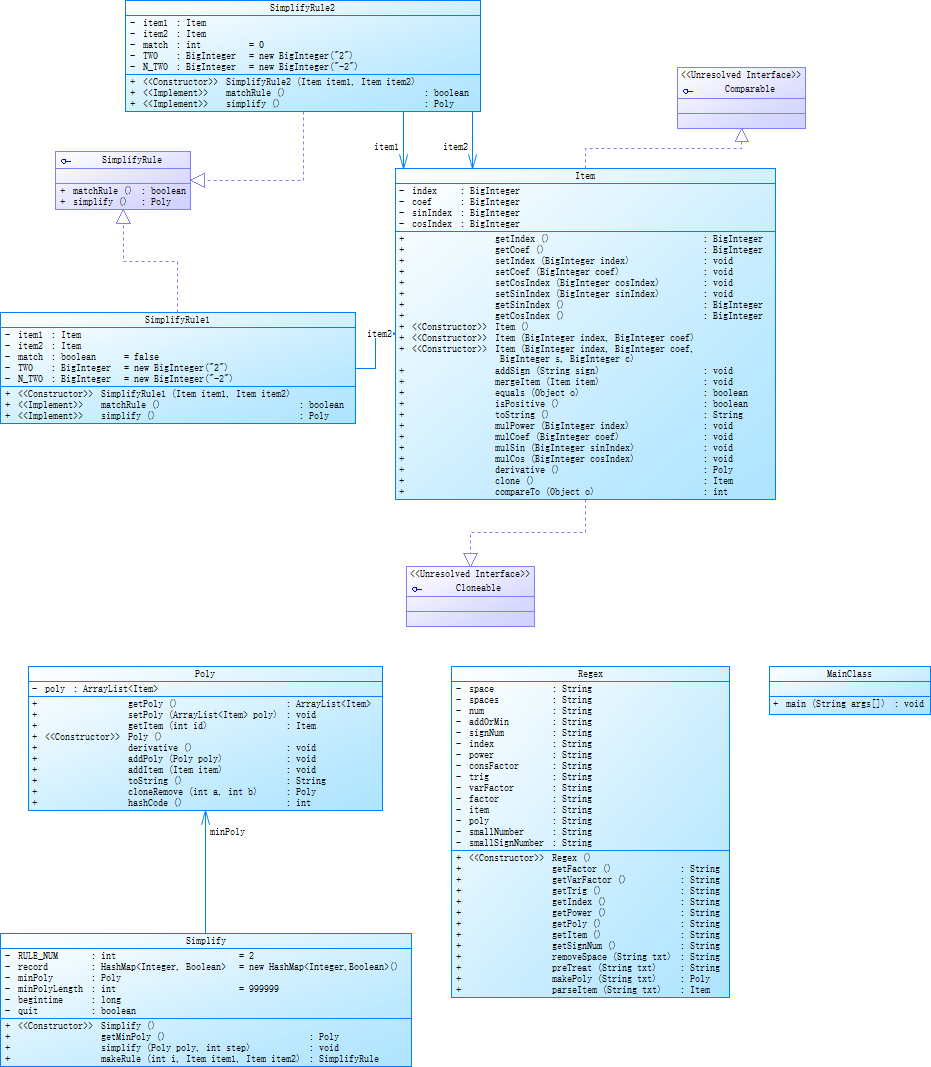
化简
第二次作业的化简,使用了深搜+熔断来实现。首先有两个化简规则,1:;2:。对当前的多项式,检验每两项是否可以用规则1或规则2进行变形,如果可以,那么进行变形,并沿此搜索下去。使用一个HashMap来记录已经得到过的表达式,并通过minPoly和minPolyLength来记录当前得到的所有表达式中最短的表达式和它的长度。如果变形后的表达式在HashMap中能找到对应,说明之前得到过了,那么回溯。每得到一个表达式,比较是否比minPoly更短,短的话将minPoly更新为当前表达式。设置了最长的搜索时间和最深递归层数,如果超过时间,那么不再搜索,输出minPoly即可。
代码度量分析
|
Type Name |
NOF |
NOPF |
NOM |
NOPM |
LOC |
WMC |
NC |
DIT |
LCOM |
|
Item |
4 |
0 |
23 |
23 |
205 |
52 |
0 |
0 |
0 |
|
MainClass |
0 |
0 |
1 |
1 |
24 |
2 |
0 |
0 |
-1 |
|
Poly |
1 |
0 |
10 |
10 |
76 |
20 |
0 |
0 |
0 |
|
Regex |
15 |
0 |
13 |
13 |
151 |
24 |
0 |
0 |
0.307692 |
|
Simplify |
6 |
0 |
4 |
4 |
64 |
16 |
0 |
0 |
0.5 |
|
SimplifyRule |
0 |
0 |
2 |
2 |
4 |
2 |
0 |
0 |
-1 |
|
SimplifyRule1 |
5 |
0 |
3 |
3 |
48 |
5 |
0 |
0 |
0 |
|
SimplifyRule2 |
5 |
0 |
3 |
3 |
74 |
10 |
0 |
0 |
0 |
Bug
第二次作业依然是在强测中被找出bug,bug是由垂直制表符引起的,我没有输出WF。后来才知道,java正则里的s不只代表空格,而是代表了、、、等空白符号。之后将“s”改为“ ”解决了bug。
找别人bug,使用了sympy进行自动测试,使用xeger产生测试数据。将发现的bug保存到单独的文件中。
反思
如果到了后边,表达式形式变得更自由,尤其是如果出现嵌套的情况,使用“三元组“就不太好办了。果然,第三次作业出现了嵌套,于是不得不重构了……..
第三次作业
题目要求
在第二次作业的基础上,加入了表达式因子;对空格格式的正确性不再保证。
实现思路
因为有了嵌套,所以原来三元组的思路不能使用了。进行了重构。Term接口,内部定义了求导、变号、合并等方法。常数项ConstTerm、幂函数项PowerTerm、三角函数项TrigTerm、连加项PlusTerm、连乘项MulTerm实现Term接口,而SinTerm和CosTerm继承TrigTerm。在可能会嵌套的地方,比如sin(),在SinTerm里存一个Term表示嵌套的内容。
如此管理数据,相当于建立了一颗树,那么使用递归完成求导操作。
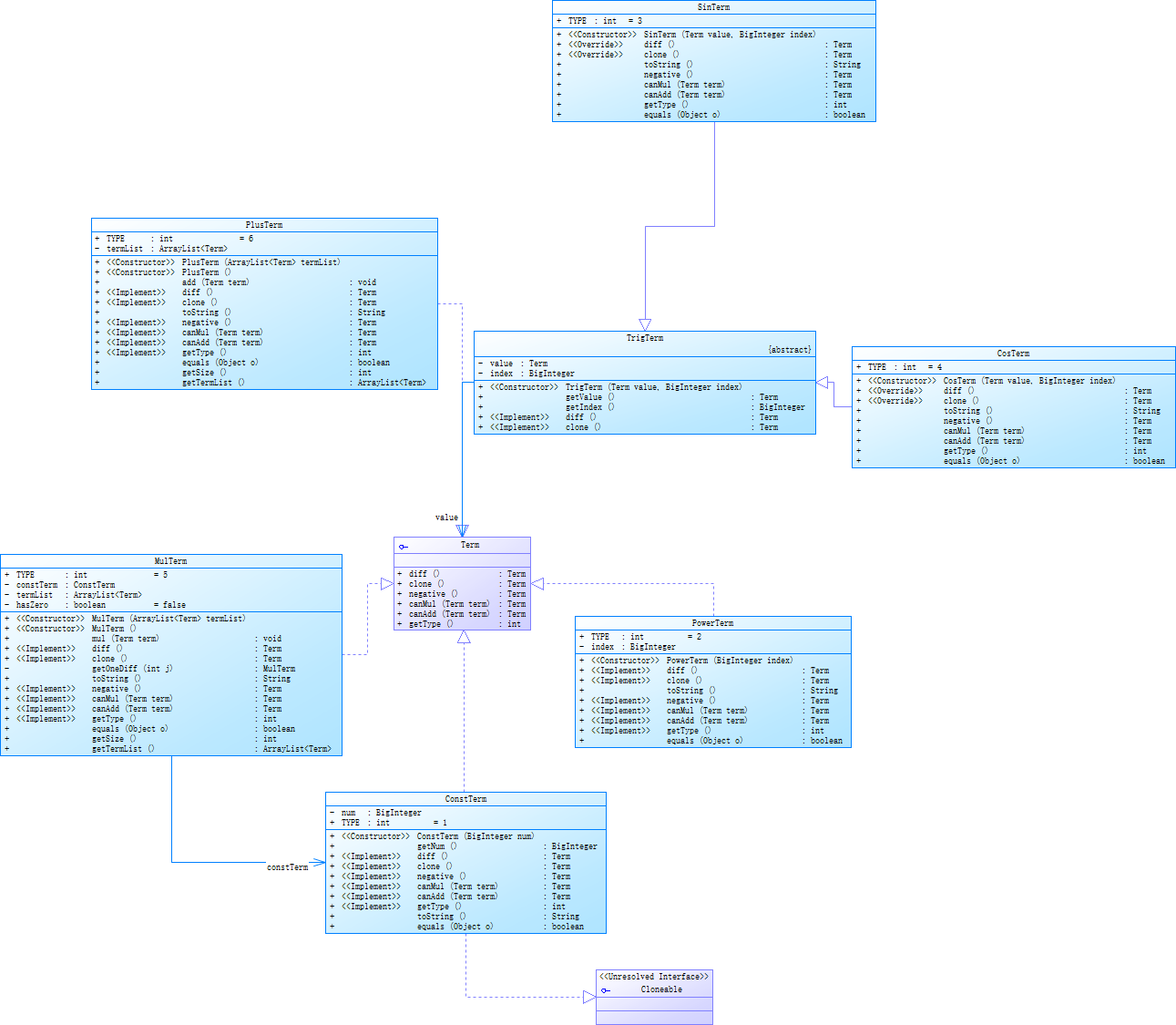
由于对空格格式的正确性不再保证,所以不可以一开始去掉所有空格,必须先验证格式正确性,再去空格。于是把格式验证分开进行。首先单独验证空格格式的正确性,因为指导书已经给出空格格式错误的所有情况,所以只需遍历这些情况,只要中了一条,就抛出异常,只有顺利通过检测,才删掉字符串中所有空格,进行下一步。
字符串解析在Analysis类中完成。由于含有嵌套括号,所以首先将每个最外层括号包含的内容,替换为特殊符号@,然后对替换后的字符串用正则来匹配。接下来使用递归解析每个@所代表的表达式。
初始化和解析类的类图如下:
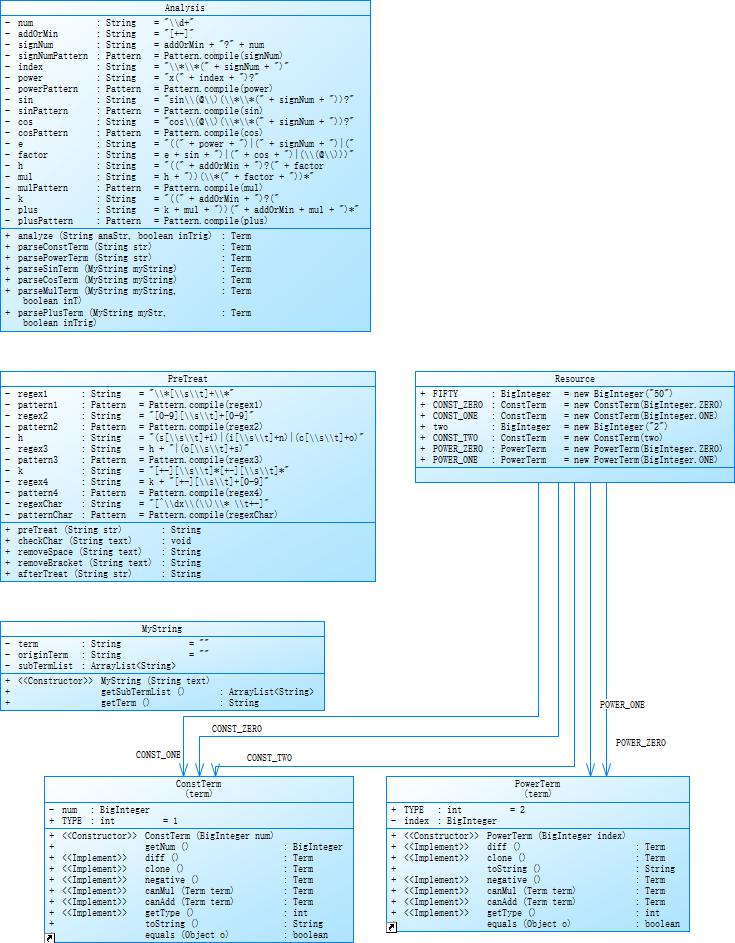
代码度量分析
|
Type Name |
NOF |
NOPF |
NOM |
NOPM |
LOC |
WMC |
NC |
DIT |
LCOM |
FANIN |
FANOUT |
|
MainClass |
0 |
0 |
1 |
1 |
25 |
1 |
0 |
0 |
-1 |
0 |
3 |
|
ConstTerm |
2 |
1 |
10 |
10 |
58 |
14 |
0 |
1 |
0.3 |
8 |
3 |
|
CosTerm |
1 |
1 |
9 |
9 |
107 |
21 |
0 |
2 |
0.666667 |
3 |
6 |
|
MulTerm |
4 |
1 |
14 |
13 |
258 |
58 |
0 |
1 |
0.142857 |
6 |
5 |
|
PlusTerm |
2 |
1 |
13 |
13 |
126 |
32 |
0 |
1 |
0.230769 |
3 |
5 |
|
PowerTerm |
2 |
1 |
9 |
9 |
78 |
17 |
0 |
1 |
0.333333 |
3 |
5 |
|
SinTerm |
1 |
1 |
9 |
9 |
104 |
21 |
0 |
2 |
0.888889 |
3 |
6 |
|
Term |
0 |
0 |
6 |
6 |
15 |
6 |
5 |
0 |
-1 |
10 |
1 |
|
TrigTerm |
2 |
0 |
5 |
5 |
23 |
5 |
2 |
1 |
0.6 |
0 |
1 |
|
Analysis |
19 |
0 |
7 |
7 |
190 |
35 |
0 |
0 |
0 |
2 |
10 |
|
MyString |
3 |
0 |
3 |
3 |
56 |
11 |
0 |
0 |
0 |
1 |
0 |
|
PreTreat |
12 |
0 |
5 |
5 |
97 |
17 |
0 |
0 |
0.4 |
2 |
1 |
|
Resource |
7 |
7 |
0 |
0 |
16 |
0 |
0 |
0 |
-1 |
7 |
2 |
Bug
本次作业被测出来的bug是,输入在cos、sin里面的表达式因子没有再嵌一层括号的时候,我没有检测出来格式错误。
找别人bug的时候,是自己构造一些特殊数据来hack。
反思
凡事要提前做,不要拖到最后。我这次提交前一小时又改了些东西,结果最后提交得非常仓促。
我将解析每种类型因子的解析方法都放在了Analysis类中,使得每次改动其中一个解析方法时,都需要满文件上下翻。如果要添加更多的因子类型(虽然后续不再有求导的作业了),就必须得在Analysis里面增加代码,这违背了开放-封闭原则。我认为更好的办法是,为每一种因子单独建立一个解析类,只负责对本因子的解析。改动一个因子的解析,只需要进入相应的类进行改动;增加一个因子,也只需增加因子类和解析类即可。和“工厂方法模式“类似。