树链剖分首先要学点预备知识LCA,树形DP,DFS序
emmmmmm..... 还要会链式前向星,线段树
树链剖分
目录
概念
- 重儿子:对于每一个非叶子节点,它的儿子中 以那个儿子为根的子树节点数最大的儿子 为该节点的重儿子
- 轻儿子:对于每一个非叶子节点,它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
- 重边:一个父亲连接他的重儿子的边称为重边
- 轻边:剩下的即为轻边
- 重链:相邻重边连起来的 连接一条重儿子 的链叫重链
- 对于叶子节点,若其为轻儿子,则有一条以自己为起点的长度为1的链
- 每一条重链以轻儿子为起点

dfs1()
这个dfs要处理的几个事情
- 标记每个点的深度deep[]
- 标记每个点的父亲father[]
- 标记每个非叶子节点的子树大小(含它自己)
- 标记每个非叶子节点的重儿子编号son[]
1 inline void dfs1(int x,int fa,int dep){ 2 deep[x] = dep; 3 father[x] = fa; 4 size[x] = 1; 5 int maxson = -1; 6 for(register int i = begin[x];i;i = next[i]){ 7 int y = to[i]; 8 if(y == fa)continue; 9 dfs1(y,x,dep+1); 10 size[x] += size[y]; 11 if(size[y] > maxson)son[x] = y,maxson = size[y]; 12 } 13 }
dfs2()
这个dfs要处理的事情
- 标记每个点的新编号
- 赋值每个点的初始值到新编号上
- 处理每个点所在链的顶端
- 处理每条链
顺序:先处理重儿子再处理轻儿子,给大家模拟一下
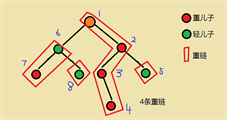
- 因为顺序是先重再轻,所以每一条重链的新编号是连续的
- 因为是dfs,所以每一个子树的新编号也是连续的
1 inline void dfs2(int x,int topf){ 2 id[x] = ++cnt; 3 a[cnt] = w[x]; 4 top[x] = topf; 5 if(!son[x])return; 6 dfs2(son[x],topf); 7 for(register int i = begin[x];i;i = next[i]){ 8 int y = to[i]; 9 if(y == father[x] || y == son[x])continue; 10 dfs2(y,y); 11 } 12 }
处理问题
- 处理任意两点间路径上的点权和
- 处理一点及其子树的点权和
- 修改任意两点间路径上的点权
- 修改一点及其子树的点权
1、当我们要处理任意两点间路径时:
设所在链顶端的深度更深的那个点为x点
- ans加上x点到x所在链顶端 这一段区间的点权和
- 把x跳到x所在链顶端的那个点的上面一个点
不停执行这两个步骤,直到两个点处于一条链上,这时再加上此时两个点的区间和即可
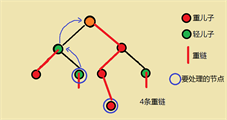
这时我们注意到,我们所要处理的所有区间均为连续编号(新编号),于是想到线段树,用线段树处理连续编号区间和
每次查询时间复杂度为O(log2n)
1 inline int query_range(int x,int y){ 2 int ans = 0; 3 while(top[x] != top[y]){ 4 if(deep[top[x]] < deep[top[y]])swap(x,y); 5 res = 0; 6 query(1,1,n,id[top[x]],id[x]); 7 ans += res; 8 ans %= mod; 9 x = father[top[x]]; 10 } 11 if(deep[x] > deep[y])swap(x,y); 12 res = 0; 13 query(1,1,n,id[x],id[y]); 14 ans += res; 15 return ans%mod; 16 }
2、处理一点及其子树的点权和:
想到记录了每个非叶子节点的子树大小(含它自己),并且每个子树的新编号都是连续的
于是直接线段树区间查询即可
时间复杂度为O(logn)
1 inline int query_son(int x){ 2 res = 0; 3 query(1,1,n,id[x],id[x]+size[x]-1); 4 return res; 5 }
区间修改就和区间查询一样的
1 inline void update_range(int x,int y,int k){ 2 k %= mod; 3 while(top[x] != top[y]){ 4 if(deep[top[x]] < deep[top[y]])swap(x,y); 5 update(1,1,n,id[top[x]],id[x],k); 6 x = father[top[x]]; 7 } 8 if(deep[x] > deep[y])swap(x,y); 9 update(1,1,n,id[x],id[y],k); 10 }
建树
既然前面说到要用线段树,那么按题意建树就可以啦!
AC代码
#include<bits/stdc++.h> using namespace std; #define Temp template<typename T> #define mid ((l+r)>>1) #define left_son root<<1,l,mid #define right_son root<<1|1,mid+1,r #define len (r-l+1) const int maxn = 2e5+5; Temp inline void read(T &x){ x=0;T w=1,ch=getchar(); while(!isdigit(ch)&&ch!='-')ch=getchar(); if(ch=='-')w=-1,ch=getchar(); while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar(); x=x*w; } int n,m,r,mod; int e,begin[maxn],next[maxn],to[maxn],w[maxn],a[maxn]; int tree[maxn<<2],lazy[maxn<<2]; int son[maxn],id[maxn],father[maxn],cnt,deep[maxn],size[maxn],top[maxn]; int res; inline void add(int x,int y){ to[++e] = y; next[e] = begin[x]; begin[x] = e; } inline void pushdown(int root,int pos){ lazy[root<<1] += lazy[root]; lazy[root<<1|1] += lazy[root]; tree[root<<1] += lazy[root]*(pos-(pos>>1)); tree[root<<1|1] += lazy[root]*(pos>>1); tree[root<<1] %= mod; tree[root<<1|1] %= mod; lazy[root] = 0; } inline void pushup(int root){ tree[root]=(tree[root<<1]+tree[root<<1|1])%mod; } inline void build(int root,int l,int r){ if(l == r){ tree[root] = a[l]; if(tree[root] > mod)tree[root] %= mod; return; } build(left_son); build(right_son); pushup(root); } inline void query(int root,int l,int r,int al,int ar){ if(al <= l && r <= ar){ res += tree[root]; res %= mod; return; } else{ if(lazy[root])pushdown(root,len); if(al <= mid)query(left_son,al,ar); if(ar > mid)query(right_son,al,ar); } } inline void update(int root,int l,int r,int al,int ar,int k){ if(al <= l && r <= ar){ lazy[root] += k; tree[root] += k*len; } else{ if(lazy[root])pushdown(root,len); if(al <= mid)update(left_son,al,ar,k); if(ar > mid)update(right_son,al,ar,k); pushup(root); } } inline int query_range(int x,int y){ int ans = 0; while(top[x] != top[y]){ if(deep[top[x]] < deep[top[y]])swap(x,y); res = 0; query(1,1,n,id[top[x]],id[x]); ans += res; ans %= mod; x = father[top[x]]; } if(deep[x] > deep[y])swap(x,y); res = 0; query(1,1,n,id[x],id[y]); ans += res; return ans%mod; } inline void update_range(int x,int y,int k){ k %= mod; while(top[x] != top[y]){ if(deep[top[x]] < deep[top[y]])swap(x,y); update(1,1,n,id[top[x]],id[x],k); x = father[top[x]]; } if(deep[x] > deep[y])swap(x,y); update(1,1,n,id[x],id[y],k); } inline int query_son(int x){ res = 0; query(1,1,n,id[x],id[x]+size[x]-1); return res; } inline void update_son(int x,int k){ update(1,1,n,id[x],id[x]+size[x]-1,k); } inline void dfs1(int x,int fa,int dep){ deep[x] = dep; father[x] = fa; size[x] = 1; int maxson = -1; for(register int i = begin[x];i;i = next[i]){ int y = to[i]; if(y == fa)continue; dfs1(y,x,dep+1); size[x] += size[y]; if(size[y] > maxson)son[x] = y,maxson = size[y]; } } inline void dfs2(int x,int topf){ id[x] = ++cnt; a[cnt] = w[x]; top[x] = topf; if(!son[x])return; dfs2(son[x],topf); for(register int i = begin[x];i;i = next[i]){ int y = to[i]; if(y == father[x] || y == son[x])continue; dfs2(y,y); } } int main(){ read(n); read(m); read(r); read(mod); for(register int i = 1;i <= n;i++)read(w[i]); for(register int i = 1,x,y;i <n;i++){ read(x); read(y); add(x,y); add(y,x); } dfs1(r,0,1); dfs2(r,r); build(1,1,n); while(m--){ int k,x,y,z; read(k); if(k == 1){ read(x); read(y); read(z); update_range(x,y,z); } if(k == 2){ read(x); read(y); printf("%d ",query_range(x,y)); } if(k == 3){ read(x); read(y); update_son(x,y); } if(k == 4){ read(x); printf("%d ",query_son(x)); } } return 0; }
完事~~~
搞定收工!!!