《排序算法系列2》选择排序

1 原理 

 选择排序(Selection sort)是一种简单直观的排序算法。
它的基本思想是：首先在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置；接着，再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

2 思路

　　(1)第一趟拿第1个元素和后面的元素依次比较,得到一个最小的元素放到第1个,此时结果第一个就是最小的元素

　　  (2)第二趟拿第2个元素和后面的元素依次比较,得到一个最小的元素放到第2个,此时结果第二个就是第二小的元素

　　  (3)第二趟拿第3个元素和后面的元素依次比较,得到一个最小的元素放到第3个,此时结果第三个就是第三小的元素

         ....依次类推

3 举例

排序流程

第1趟：i=0。找出a[1...5]中的最小值a[3]=10，然后将a[0]和a[3]互换。 数列变化：20,40,30,10,60,50 -- > 10,40,30,20,60,50
第2趟：i=1。找出a[2...5]中的最小值a[3]=20，然后将a[1]和a[3]互换。 数列变化：10,40,30,20,60,50 -- > 10,20,30,40,60,50
第3趟：i=2。找出a[3...5]中的最小值，由于该最小值大于a[2]，该趟不做任何处理。
第4趟：i=3。找出a[4...5]中的最小值，由于该最小值大于a[3]，该趟不做任何处理。
第5趟：i=4。交换a[4]和a[5]的数据。 数列变化：10,20,30,40,60,50 -- > 10,20,30,40,50,60

选择排序动态演示

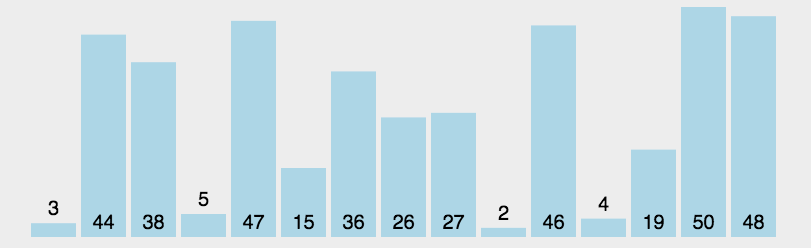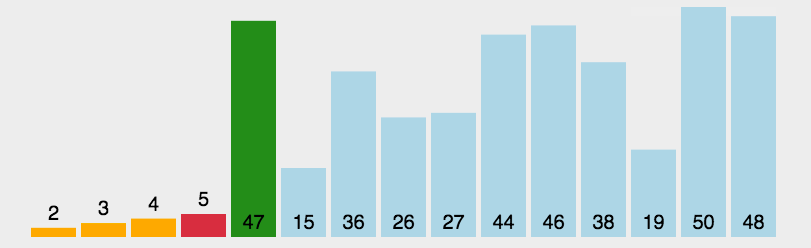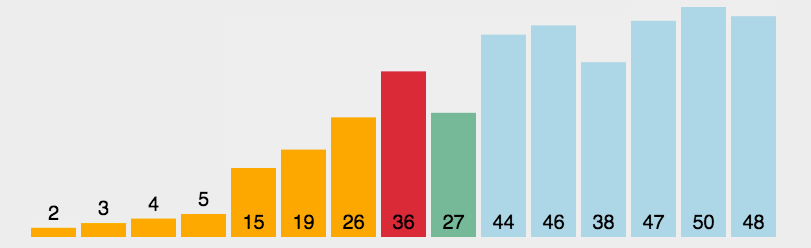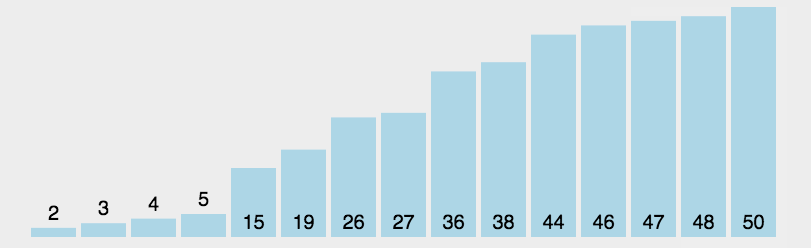
 4 代码实现

     public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length-1; i++) {
            //记录最小值的索引,第一次为第每次需要比较的第一个元素
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                //拿最小值和后面的元素比较
                //注意这里一定要用arr[minIndex],不能使用arr[i]
                if (arr[minIndex] > arr[j]) {
                    minIndex = j;
                }
            }
            //辅助变量
            int temp;
            if (minIndex != i) {//如果minIndex等于i  证明后面没有数比前面小
                temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }
    }

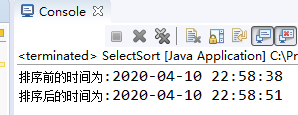
5 选择排序速度测试

    //选择排序
    //选择排序的时间复杂度 O(n^2)
    public static void main(String[] args) {
　　　　 //随机定义80000个数组
        int [] arr2 = new int[80000];
        //随机添加数字
        for (int i = 0; i < arr2.length; i++) {
            arr2[i] = (int)(Math.random()*800000);
        }
        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        Date date1 = new Date();
        String time1 = simpleDateFormat.format(date1);
        System.out.println("排序前的时间为:" + time1);
        
        selectSort(arr2);
        
        Date date2 = new Date();
        String time2 = simpleDateFormat.format(date2);
        System.out.println("排序后的时间为:" + time2);
    }
    
    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length-1; i++) {
            //记录最小值的索引,第一次为第每次需要比较的第一个元素
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                //拿最小值和后面的元素比较
                //注意这里一定要用arr[minIndex],不能使用arr[i]
                if (arr[minIndex] > arr[j]) {
                    minIndex = j;
                }
            }
            //辅助变量
            int temp;
            if (minIndex != i) {//如果minIndex等于i  证明后面没有数比前面小
                temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }
    }

速度测试结果

80000个数字排序大约需要4秒

16万数字排序大约需要13秒