Eigen学习之简单线性方程与矩阵分解

　　Eigen提供了解线性方程的计算方法，包括LU分解法，QR分解法，SVD（奇异值分解）、特征值分解等。对于一般形式如下的线性系统：

　　　　　　　　

　　解决上述方程的方式一般是将矩阵A进行分解，当然最基本的方法是高斯消元法。

　　先来看Eigen 官方的第一个例程：

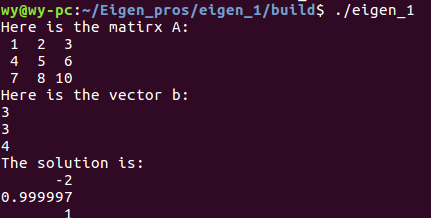
#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main()
{
    Matrix3f A;
    Vector3f b;
    A << 1,2,3, 4,5,6, 7,8,10;
    b << 3,3,4;
    cout<<"Here is the Matrix A:
"<< A <<endl;
    cout<<" Here is the vector b:
"<< b <<endl;
    Vector3f x = A.colPivHouseholderQr().solve(b);
    cout<<"The solution is:
"<<x<<endl;
    return 0;
}

运行结果如下：

Eigen内置的解线性方程组的算法如下表所示：

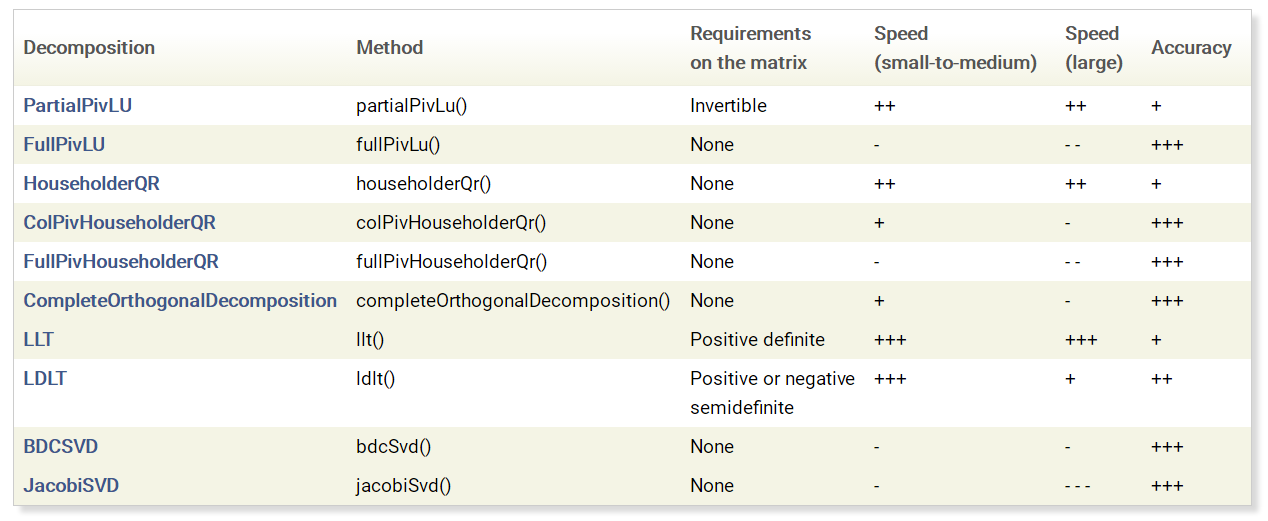
使用这些接口也可以解决矩阵相乘的问题：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main()
{
    Matrix2f A,b;
    A << 2,-1,-1,3;
    b << 1,2,3,1;
    cout<<"Here is the matrix A:
"<<A<<endl;
    cout<<"Here is the right hand side b:
"<<b<<endl;
    Matrix2f x = A.ldlt().solve(b);
    cout<<"The solution is:
"<<x<<endl;
    return 0;
}

运行结果如下：

Eigen也提供了计算特征值和特征向量的算法：

下面是一个简单的例子：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main()
{
    Matrix2f A;
    A << 1,2,2,3;
    cout<<"Here is the matrix A:
"<<A<<endl;
    SelfAdjointEigenSolver<Matrix2f> eigensolver(A);
    if( eigensolver.info() != Success ) abort();
    cout<<" The eigenvalues of A are:
"<<eigensolver.eigenvalues()<<endl;
    cout<<" Here is a matrix whose columns are eigenvectors of A
"
        <<" corresponding to these eigenvalues:
"
        <<eigensolver.eigenvectors()<<endl;
    return 0;
}

运行结果如下：

Eigen 也提供了求逆矩阵和求矩阵行列式的算法，但是这两种算法对于大型矩阵来说都是非常不经济的算法，当需要对大型矩阵做这种的操作时，需要自己判断到底需不需这样做。但是对于小型矩阵 则可以没有顾虑地使用。

下面是一个例子：

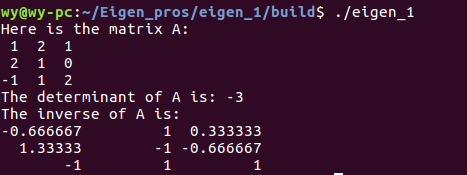
#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main()
{
    Matrix3f A;
    A << 1,2,1,
         2,1,0,
         -1,1,2;

    cout<<"Here is the matrix A:
"<<A<<endl;
    cout<<"The determinant of A is "<<A.determinant()<<endl;
    cout<<"The inverse of A is:
"<<A.inverse()<<endl;
    return 0;
}

运行结果如下：

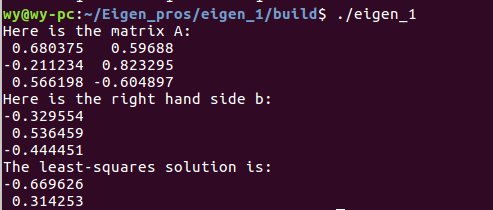
Eigen也提供了解最小二乘问题的解法，并给出两种实现，分别是BDCSVD和JacobiSVD,其中推荐使用的一种是BDCSVD。下面是一个例子：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main()
{
    MatrixXf A = MatrixXf::Random(3,2);
    cout<<"Here is the matrix A:
"<<A<<endl;
    VectorXf b = VectorXf::Random(3);
    cout<<"Here is the right hand side b:
"<<b<<endl;
    cout<<"The least-squares solution is:
"
        <<A.bdcSvd(ComputeThinU|ComputeThinV).solve(b)<<endl;
    return 0;
}

运行结果如下：