Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition
2018-01-28 15:45:13
研究背景和动机:
行人动作识别(Human Action Recognition)主要从多个模态的角度来进行研究,即:appearance,depth,optical-flow,以及 body skeletons。这其中,动态的人类骨骼点 通常是最具有信息量的,且能够和其他模态进行互补。但是最近研究这个东西的工作,却很少,我们系统的分析了这个模态,目标就是想开发一种 principle and effective 的方法来建模动态的骨骼点,并且将其用于行为识别。
动态的骨骼模态,可以自然地表达为时间序列的 human joint locations,行人的动作,就可以看做是分析这些运动模式就可以了。当前的方法主要是简单的将 the joint coordinates 构成特征向量,然后应用 temporal analysis thereon。这些方法的能力是有限的,因为他们并没有显示的探索这些 joints 之间的空间关系,然而这对于理解 human actions 来说,是非常重要的。最近也有些方法将这些连接考虑到他们的模型中,但是,这些方法严重的依赖于手工设计的 parts 或者 rules。这就使得他们的方法很难应用到其他问题上。
为了克服这些困难,我们需要一种新的方法可以自动的捕获 the patterns embedded in the spatial configuration of the joints, 以及 their temporal dynamics。这是深度神经网络的优势,但是,骨骼点的数据是一种 graph 的结构,而不是 2D 或者 3D 的网格,所以,很难利用当前的 CNN 来直接处理这些数据。最近,graph convolutional networks(GCNs),将 CNN 拓展到了 任意结构的 graphs 上来,已经得到了很大的关注,并且得到了广泛的应用,如:image classification, document classification, and semi-supervised learning. 但是,这些方法都是基于一种 fixed graph 作为输入。将 GCNs 在大型数据集上来建模 dynamic graphs,如:human skeleton sequence,还没有被研究。
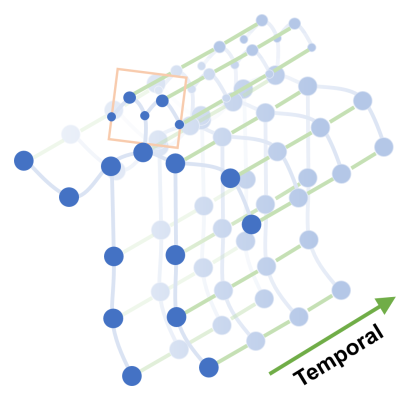
本文通过将 GCN 拓展到 spatial-temporal graph model,称为:ST-GCN。如上图所示,这个模型是在 一个骨骼图的序列上 构建的,每个节点对应了 a joint of the human body。有两种 edges,即:spatial edges 和 temporal edges。
本文的创新点:
1). We propose ST-GCN, a generic graph-based formulation for modeling dynamic skeletons, which is the first that applies graph-based neural networks for this task.
2). We propose several principles in designing convolution kernels in ST-GCN to meet the specific demands in skeleton modeling.
3). On two large scale datasets for skeleton-based action recognition, the proposed model achieves superior performance as compared to previous methods using hand-crafted parts or traversal rules, with considerably less effort in manual design.
The code and models of ST-GCN are made publicly available https://github.com/yysijie/st-gcn.
将 GCNs 拓展到 graph 上主要有如下两大类方法:
1). the spectral perspective, where the locality of graph convolution is considered in the form of spectral analysis;
2). the spatial perspective, where the convolutioan filter are applied directly on the graph nodes and their neighbors.
3 Spatial Temporal Graph ConvNet
3.1. Pipeline Overview:
基于骨骼的数据可以通过捕获运动的设备,或者 视频中姿态估计的算法得到。通常,这些数据是序列的视频帧,每一帧都有关节点坐标的结合。给定 2D 或者 3D 坐标的形式,关节点的序列,我们构建一个时空图(spatial temporal graph),其中,关节点是 graph nodes,人体结构 以及 时间 的自然连接作为 graph 的 nodes。ST-GCN 的输入是 graph nodes 的的联合坐标向量。这个可以类比 基于图像的 CNNs ,其输入是 pixel intensity vectors residing on the 2D image grid。时空图卷积操作的多层,将会用来处理这些数据,然后在 graph 上,产生高层的 feature maps。然后用标准的 SoftMax 分类器来进行分类。整个模型是 end to end trained,并可以用 BP 算法进行优化。

3.2. Skeleton Graph Construction:
我们构建一个无向图 G = {V, E},其有 N 个节点,T frame是 featuring both intra-body and inter-frame connection。
在一个 graph 中,节点的集合 $ V = {vti|t=1,..,T} $ includes the all the joints in a skeleton sequence。作为 ST-GCN's 的输入,节点 F(vti) 的特征向量是由 坐标向量 以及 预测的置信度构成的。我们在骨骼序列上构建 spatial-temporal graph 是有两个步骤:
首先,在一帧上的节点,我们按照人体结构的连接性,用 edge 将其连接起来;
然后,每一个节点,会在连续视频帧上,会被连接到相同的节点。
正式的来说,the edge set E 是有两种子集合的:
the first subset depicts the intra-skeletion connection at each frame;![]()
the second subset contains the inter-frame edges,which connect the same joints in consecutive frames。![]()
3.3. Spatial Graph Convolutional Neural Network:
在我们进入完全的 ST-GCN 之前,我们首先看单帧上的 graph CNN model。在这种情况下,在时刻 t ,单张视频帧的情况下,将会有 N 个骨骼节点 $V_t$,并且有骨骼边界(the skeleton edges)。我们回忆在 2D 自然图像或者 feature maps 上的卷积操作,卷积操作的输出仍然是 2D 的网格。当步长为1,并且设置合适的 padding 时,输出的 feature maps 可以和输入拥有相同的大小。我们在接下来的讨论中,都是基于这个假设。给定一个 kernel size 为 K*K 的卷积操作,通道个数为 c 的输入 feature maps,在位置 x 处的单个通道的输出值为:

其中, P 是 采样函数(the sampling function p),列举了位置 x 的近邻(enumerates the neighbors of location x)。在图像卷积中,也可以表示为:$p(x, h, w) = x + p' (h, w)$。加权函数(the weight function w)提供了一个权重向量,来计算其与采样的输入向量的内积(provides a weight vector in c-dimensional real space for computing the inner product with the sampled output feature vectors of dimension c)。由于加权函数与位置 x 无关,所以,滤波器的权重可以在图像中进行共享。在图像领域,标准的卷积在图像领域可以通过编码矩形网格(rectangle grid)。更加细节的解释和应用可以参考 Dai et al. 2017 的文章。
在 graph 上的卷积操作可以定义为:将上述定义拓展到存在于 spatial graph $V_t$ 的输入特征图上,即:the feature map has a vector on each node of the graph(在 graph 上的每个节点都有一个向量)。下一步的拓展,就是重新定义采样函数 p 和 加权函数 w。
Sampling function. 在图像中,采样函数 p(h, w) 是定义在中心位置为 x 的近邻像素上的。在 graph 中,我们可以类似的定义采样函数在一个节点 $v_{ti}$ 的近邻集合 $B(v_{ti})$ 。所以采样函数 p 可以写为:
![]()
在本文当中,我们对于所有的情况,都设置 D = 1,即:1-neighbor set of joint nodes. 更多数量的 D 留作未来工作。
Weight function. 相对于采样函数,加权函数的定义更加 trickier。在 2D 卷积中,一个固定的 grid 自然的存在于中心位置(naturally exists around the center location)。所以,相邻像素点拥有一个固定的空间次序(pixles within the nighbor can have a fixed spatial order)。The weight function can then be implemented by indexing a tensor of (c, K, K) dimensions according to the spatial order. 像我们刚刚创建的那种 general 的 graph,并没有这样的潜在的排列(there is no such implicit arrangement)。该问题首先被 Niepert et al. 研究,the order 定义为:a graph labeling process in the neighbor graph around the root node. 我们跟随这个 idea 来构建我们的权重函数。并非给定每一个近邻节点一个特定的 labeling,我们简单的将骨骼节点的近邻集合划分为固定个数的 K 个子集,每一个子集有一个 label。于是,我们有了一个映射,即:maps a node in the neighborhood to its subset label. 加权函数 w 可以索引一个 tensor (c, K) dimension 来执行:

Spatial Graph Convolution. 有了优化的采样函数和加权函数,我们可以重新定义公式(1)为:
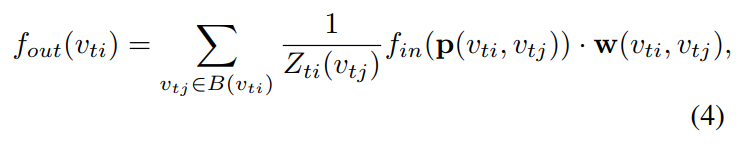
其中,the normalizing term Z 等于对应子集的基数。用公式(2)(3)代替公式(4)中的各项,我们可以得到:
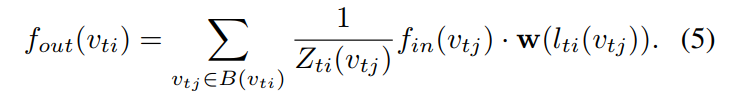
值得注意的是,这个表达形式也可以看做是标准的 2D convolution,如果我们将 image 看做 常规的 2D grid(this formulation can resemble the standard 2D convolution if we treat a image as a regular 2D grid)。
Spatial Temporal Modeling. 在上述 Spatial graph CNN 的基础上,我们现在开始将其拓展都 时空结构上。在构建 graph 的时候,graph 的 temporal aspect 我们是直接时序上相同的节点连接起来的。这确保我们可以定义一种非常简单的策略将 Spatial graph CNN 拓展到 spatial temporal domain。我们将近邻节点拓展到包含时序连接的节点(we extend the concept of neighborhood to also include temporally connected joints):
![]()
为了完成在 spatial temporal graph 上的卷积操作,我们也需要 the sampling function,and the weight function. 因为 temporal axis 的次序是显然的,我们直接将 label map $l_{ST}$ 定义为:
![]()
3.4. Partition Strategies .
给定 spatial temporal graph convolution 的高层定义,设计一种 partitioning strategy 来执行 the label map l.
Uni-labeling.
Distance partitioning.
Spatial configuration partitioning.
3.5. Learnable edge importance weighting.
3.6. Implementing ST-GCN.
基于 graph 的卷积操作不如 2D 或者 3D 卷积那么直观,这里我们采取类似 Kipf 在 ICLR 2017年发表的文章中所用的 graph convolution 操作。同一帧的 Body 内部的关节点的连接可以表示为:a adjcency matrix A,然后用 identity matrix I 用来表示 self-connections。在 single-frame 的情况下,用第一种分割策略的 st-gcn 可以用下面的公式进行表达:
![]()
其中,多个输出通道的权重向量堆叠起来构成了权重矩阵(the weight matrix W)。实际上,在时空的情况下,我们可以将 input feature map 表示为:a tensor of (C, V, T) dimension. graph convolution 可以通过执行 1 × Γ standard 2D convolution and multiplies the resulting tensor with the normalized adjacency matrix on the second dimension.
对于多个子集的划分策略(for partitioning strategies with multiple subsets),即:distance partitioning and spatial configuration partitioning,我们也这么执行。 但注意到,邻接矩阵被分解为多个矩阵 Aj,即: $A+I = sum_{j} A_j$。
执行 learnable edge importance weighting 是很直观的。对于每一个邻接矩阵,我们给其配置一个可学习的 weight matrix M。

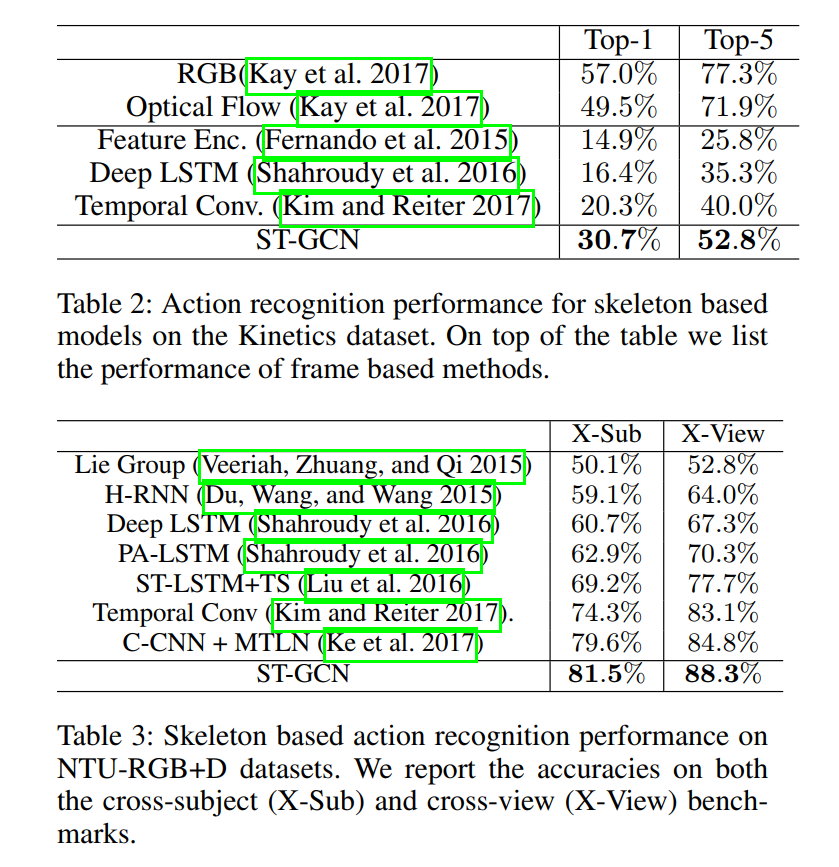
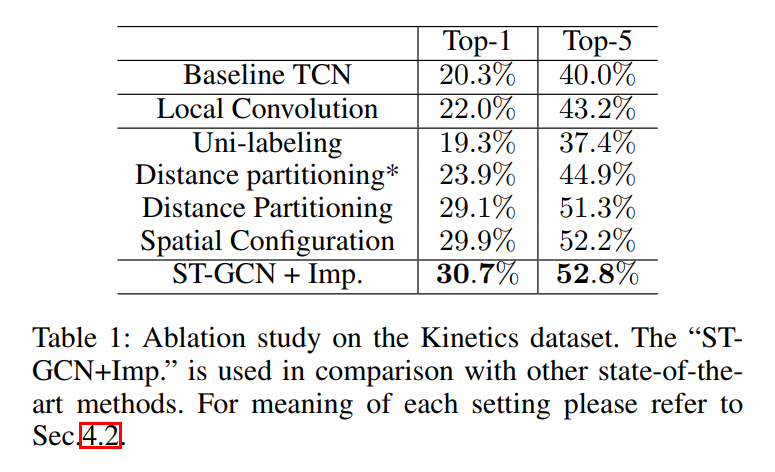
Experiments: