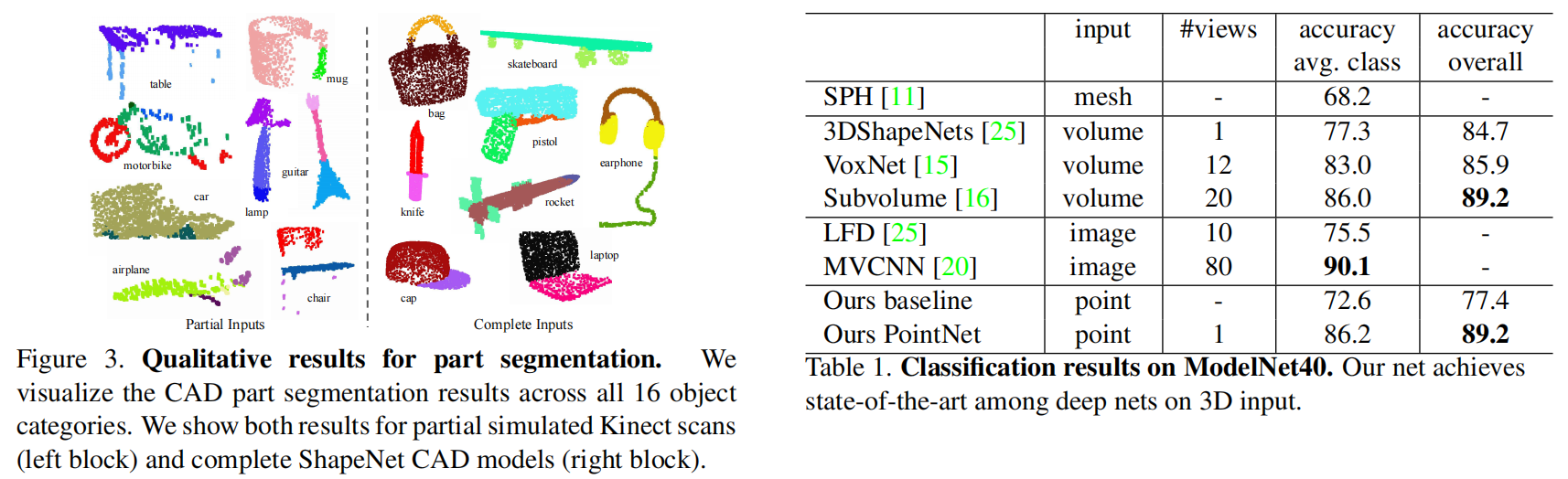
- Unordered: 点云并没有特定的序列。
- Interaction among points: 点并不是孤立的,近邻的点构成了一个有意义的子集。
- Invariance under transformation: 因为是一个几何体,学习到的表达应该是与形变无关的。对物体进行旋转后,物体的类别或者点的划分应该是不变的。
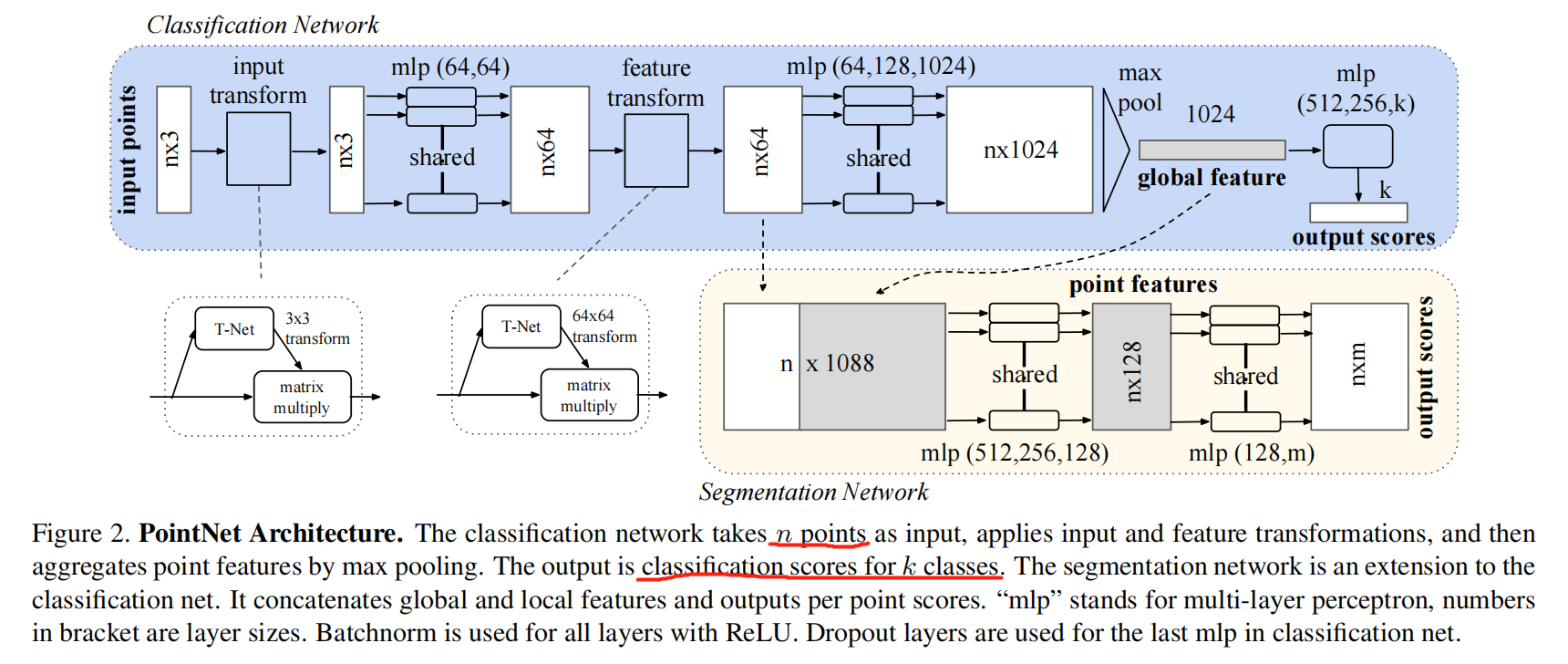
1.2. PointNet Architecture:
如上图所示,PointNet 包含三个主要模块:
- the max-pooling layers 作为一个 对称函数来聚合所有点的信息;
- a local and global information combination structure;
- two joint alignment networks 可以对齐输入点和点特征;
1.2.1. Symmetric Function for Unordered Input:
为了使得模型对输入具有不变性,有三个策略可以选择:1. 将输入排序为规范的次序;2. 将输入看做是一个序列,来训练一个 RNN 模型,但是用各种扰动的策略来增强训练数据;3. 利用一个简单的对称函数来从每一个点来聚合信息。此处,一个对称函数将 n 个向量作为输入,并输出一个新的向量并对输入序列无感。例如,+ 和 * 代表对称二元函数。
作者进行了一波分析,最终根据自己的实验分析以及前人的工作,排除掉了 1 和 2 两种做法。作者想通过一种 general function 的方式,进行处理。通过在集合上,采用对称函数:
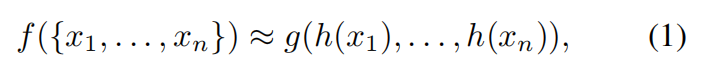
其中,f, h, g 都是对称函数。
经验上来说,作者的基础模型非常简单:通过一个 MLP 来预测 h,用单个变量函数和max-pooling function 来预测 g。实验发现,这种方式可以得到不错的效果。通过收集 h,就可以学习一组 f's 来捕获不同的集合属性。
1.2.2. Local and Global Information Aggregation:
通过上述函数得到一组向量 [f1, f2, ... , fK],这是输入集合的全局特征。可以简单地利用 SVM 或者多层感知机分类器进行分类。但是,点的分割,一般来说都需要 local 和 global 知识的组合。
作者提出的方案如图 2 所示,在计算全局点云特征向量后,作者将其返回到每一个点特征,然后将全局特征与每一个点特征进行拼接。然后,对组合后的点特征,提取新的点特征,此时,每一个点特征均具有了局部和全局的信息。有了这个小的改动,PointNet就可以基于局部集合和全局语义信息进行点的预测。
1.2.3. Joint Alignment Network:
作者还希望学习到的特征能够对某些集合形变,具有一定的抵抗能力。作者利用一个小网络来预测一个放射变换矩阵,然后直接将该转换应用到输入点的坐标上。该小网络本身和大网络很像,是由与点无关的特征提取构成的,max-pooling 和 FC layer。这个想法也可以拓展到特征空间的对齐上。可以将另外一个 alignment network 插入到 point features 上,然后预测一个特征转换矩阵来从不同的输入点云来对齐特征。然而,在特征空间进行矩阵的转换,比空间转换矩阵具有更高的空间,这将会极大的增加优化的难度。作者因此添加了一个正则化项,到 softmax training loss,约束 feature transformation matrix 和 orthogonal matrix 尽可能的接近:
![]()
其中, A 是一个 mini-network 预测的特征对齐网络。作者通过实验发现,该正则化项可以明显使得训练变得平稳,模型也取得了更好的结果。