AdaScale: Towards real-time video object detection using adaptive scaling
2019-02-18 16:14:17
Paper: https://www.sysml.cc/papers.html
本文提出一种新的技术,AdaScale,来改善视频中物体检测的尺度问题,在提升速度的同时,改善了精度。
作者的实验发现在降低图像分辨率的时候,部分图像的识别精度就会得到改善,并且给出了结果展示:

那么是什么原因导致这种情况呢?作者给出了如下的解释:
i) Reducing the number of false positives that may be introduced by focusing on unnecessary details.
ii) Increasing the number of true positives by scaling the objects that are too large to a size at which the object detector is more confident.
受到这种现象的启发,作者提出通过 “re-size” 图像的方式以得到其最优的 scale,来提升检测的速度和精度。所以,本文提出 AdaScale 来根据当前帧的信息来预测下一阵的最佳的 scale。并且在 ImageNet VID 和 mini YouTube-BB datasets 上同时提升了速度和精度。
其训练和测试过程,如下图所示:

3.1. Optimal Scale:
作者首先定义一个 scale 集合 {600,480,360,240} ,并且定一个度量标准来衡量不同尺寸的检测效果。作者这里采用的是最终的 loss function。总得来说,物体检测的损失函数可以分为包围盒的回归和分类损失:
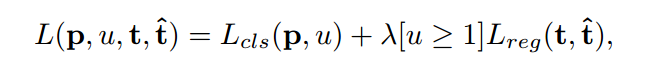
但是,直接用这种方法,也有一个 bug:对于重合度较低的 proposal,会自动归类为 background,该损失函数自动将 regression loss 设置为 0,直接用该指标衡量不同图像尺寸会支持含有较少前景包围盒的图像尺寸(will favor the image scale with fewer foreground bounding boxes)。
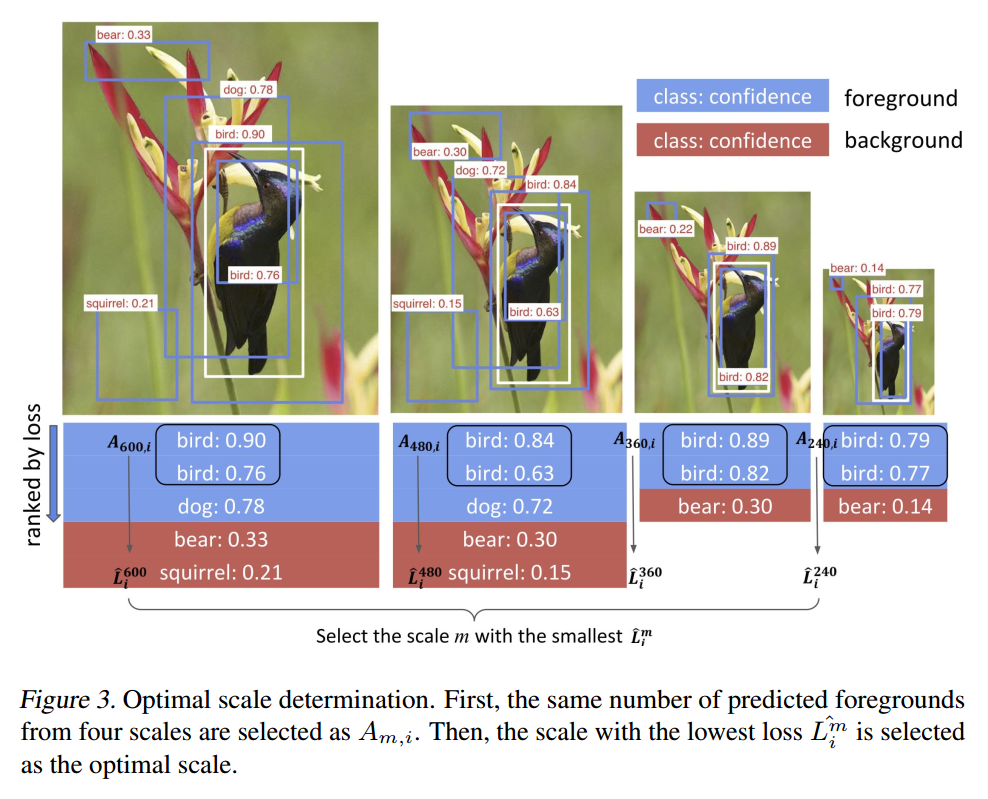
所以,为了处理该问题,作者提出一种新的度量方法来聚焦于拥有相同数量的前景包围盒,来比较不同的图像尺寸。具体来说,
用 $L^m_{i, a}$ 表示 利用上述公式计算得到的 image i 的预测包围盒 a 在 scale m 的损失;
$hat{L_i^m}$ 表示图像 i 在尺寸 m 的损失,作为我们的提出的指标。
为了得到 $hat{L_i^m}$,我们首先计算预测的前景包围盒的数量 $n_{m, i}$,对于图像 i 的每一个尺寸 m,使得 $n_{min, i} = min_{m}(n_{m, i}).$
所以,所提出的度量标准可以通过如下的方法计算得到:
![]()
为了得到 $A_{m, i}$,对于每一个 scale,我们对预测的前景包围盒进行排序,并且挑选出前 $n_{min, i}$ 添加到 $A_{m, i}$。
有了这个度量标准,我们就可以定义最优尺寸:
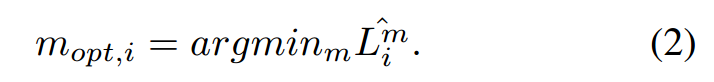
3.2. Scale Regressor:
作者采用的 RFCN 是依赖于最后一层卷积层特征的,作者认为该深度特征的通道已经包含了尺寸的信息。所以,可以利用该深度特征直接构建 scale regressor 来预测最优的尺寸,如图4所示。
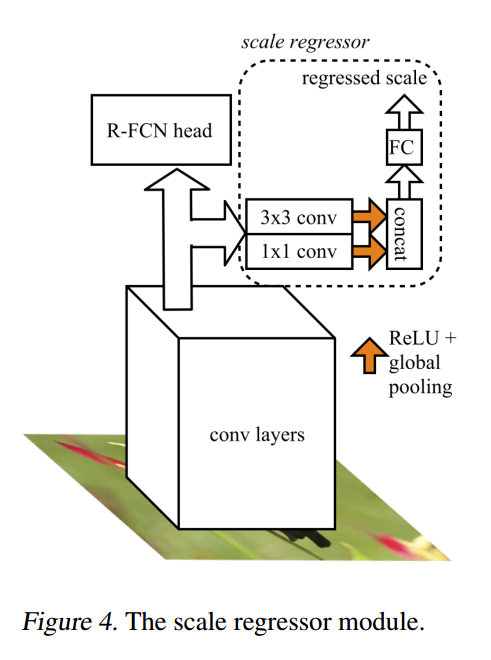
作者用 1*1 卷积来捕获不同特征图的尺寸信息 (the size information from different feature maps),用 3*3 卷积来捕获特征图上的复杂度(the complexity of each 3*3 patch in the fature maps)。这些特征在经过 ReLU 和 global pooling 之后,进行组合,输入到 fc 层,进行回归。需要注意的是,本文不是直接进行最优尺寸的估计,而是回归一个相对尺寸,使得模型可以学会 react (up-sample,down-sample,or stay the same)。对于图像 i 来说,回归尺寸的目标是:
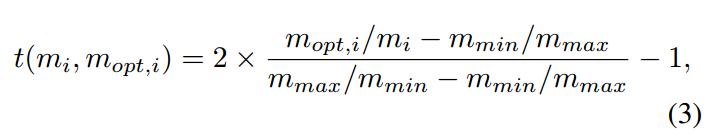
其中,$m_i$ 是 是图像 i 的尺寸,$m_{min}$ 是定义的最小尺寸,$m_{max}$ 是定义的最大尺寸。所以,我们是要回归出一个归一化的范围(relative scales): [-1, 1]。
在训练数据集上,我们利用公式(2)得到需要回归的标签。并且采用均方误差来进行回归:
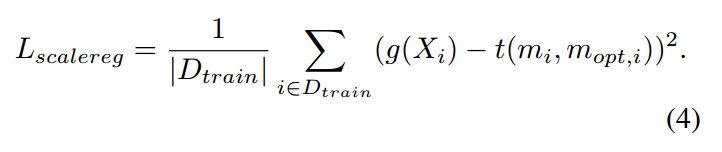

==