DS博客作业03--树

0.PTA得分截图

1.本周学习总结（0-5分）

1.1 总结树及串内容

• 串的BFKMP算法
  串是由0个或者多个字符所组成的有限序列，串可以采用顺序存储和链式存储两种方式，在主串中查找子串问题是串的一个非常重要的问题，这类问题有两种算法：Brute-Force算法，简称BF算法和KMP模式匹配算法。
• BF算法
  BF算法是一种常规算法，子串的第一个字符与主串的第一个字符进行比较，若相等，则继续比较主串与子串的下一个字符，若不相等，子串的第一个字符与主串的第二个字符进行比较，依次比较下去，直到全部匹配。
  第一轮
  
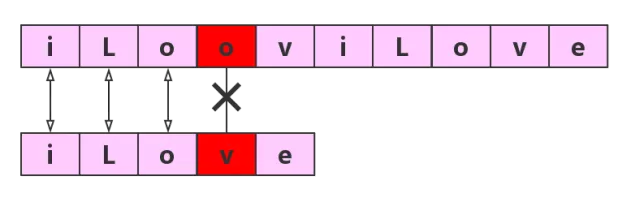
  第二轮
  
  ······
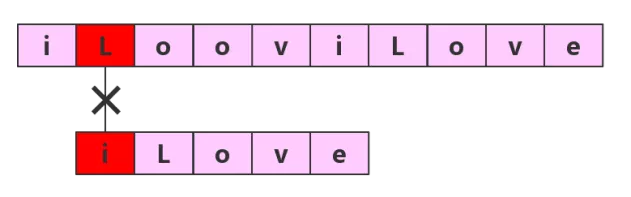
  第五轮
  
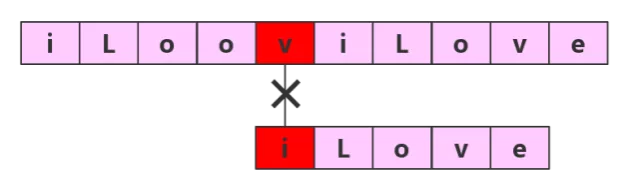
  第六轮
  
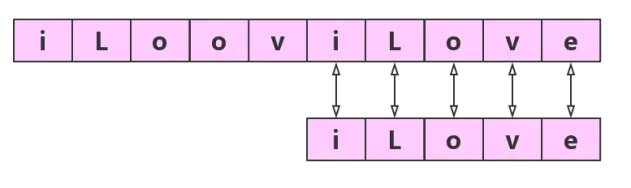
  匹配成功，返回子串在主串中第一次出现的位置，匹配失败返回 -1。
  代码实现

int BF(String s,String t)
{
   int i=j=0;
   while(i<s.length&&j<t.length)
   {
       if(s.data[i]==t.data[j])
       {
          i++;j++;
       }
       else
       {
          i=i-j+1;
          j=0;
       }
   }
   if(j>=t.length) return (i-t.length);
   else return -1;
}

• KMP算法
  当数据量比较小时，BF算法还可以用，但当数据量很大时，BF算法就显得很耗时了，我们就可以用KMP算法了。KMP算法是由 D.E.Knuth，J.H.Morris，V.R.Pratt 提出的，它是一种对BF算法的改进，它减少了子主串的匹配次数，主串指针一直往后移动，子串指针回溯，主串不需回溯。
  如图所示直到第六个元素才配对失败，由于子串的前三个元素都不相同，所以子串与主串中的二和三两个元素一定是不匹配的，可以直接和主串的第四个元素开始配对。
  

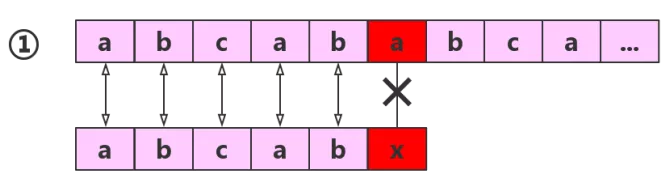
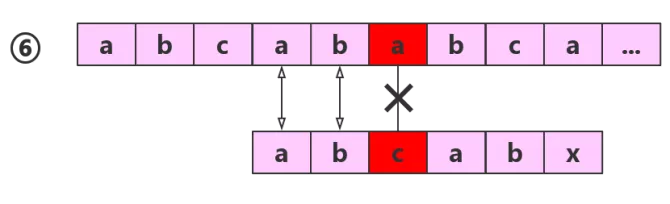
因为子串中的1和2元素和4和5元素是相同的，而且还和主串配对成功了，那么子串中1和2元素一定与主串的4和5元素配对，所以可以直接进行如下图的操作。

next数组
next数组是存放失配时，模式串下一次匹配位置，取值如图所示。

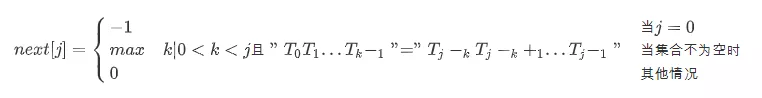
求next数组代码实现

void getNext(String t, int next[]) 
{
    int j = 0, k = -1;
    next[0] = -1;
    while (j < t.length - 1)
    {
        if ((k == -1) || t.data[j] == t.data[k])
        {
            j++;k++;
            next[j] = k;
        }
        else  k = next[k];
    }
}

KMP算法代码实现

int KMP(String s,String t)
{
    int next[Max],i=j=0;
    getNext(t,next);
    while(i<s.length&&j<t.length)
    {
       if(j==-1||s.data[i]==t.data[j])
       {
           i++;j++;
       }
       else  j=next[j];
    }
    if(j>=t.length)  return (i-t.length);
    else return -1;
}

nextval数组
next数组也有需要改进的地方，当匹配字串时，有连着的多个相同的字符时，会重复操作同一个字符，比如s为aaabaaaab，t为aaaa时，因为前三个都是一样的，就没有必要重复做一种操作，所以我们可以定义一个nextval数组，避免做相同的操作。
nextval数组代码

void getNextval(String t, int nextval[])
 {
    int i = 0, j = -1;
    nextVal[0] = -1;
    while (i < t.length)
    {
        if ((k == -1) || (t.data[i] == t.data[j]))
        {
            i++;j++;
            if (t.data[i] != t.data[j])
                nextval[i] = j;
            else
                nextval[i] = nextval[j];
        }
        else 
            j = nextval[j];
    }
}

修改后的KMP算法代码实现

int KMP(String s,String t)
{
    int nextval[Max],i=j=0;
    getNextval(t,nextval);
    while(i<s.length&&j<t.length)
    {
       if(j==-1||s.data[i]==t.data[j])
       {
           i++;j++;
       }
       else  j=nextval[j];
    }
    if(j>=t.length)  return (i-t.length);
    else return -1;
}

• 二叉树存储结构、建法、遍历及应用
• 二叉树存储结构：顺序存储结构，二叉链表
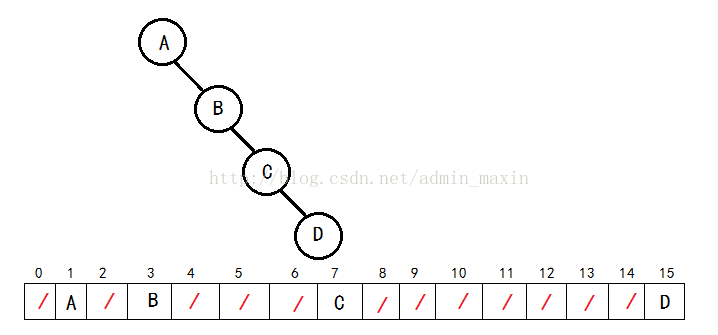
  顺序存储结构：顺序存储就是把一串字符串存储在数组里面，根据下标来确定父亲和孩子的关系，一般对于一个i结点来说，父亲是i/2，左孩子是2i，右孩子是2i+1。这种存储结构有一定的缺点，就是空间利用率太低，一般只适用于完全二叉树，如图。
  

二叉链表：因为二叉树每个结点都有左孩子、右孩子，所以可以用一种链式存储结构来存放数据，这种结构内有结点数据，左孩子指针和右孩子指针。

typedef struct BinTNode
{
	ElemType data;
	struct BinTNode *lchild,*rchild;
} BinTNode,*BinTree;

• 二叉树建法：顺序存储结构转二叉链，先序遍历，先序+中序序列，中序+后序序列
  顺序存储结构转二叉链：
  
  
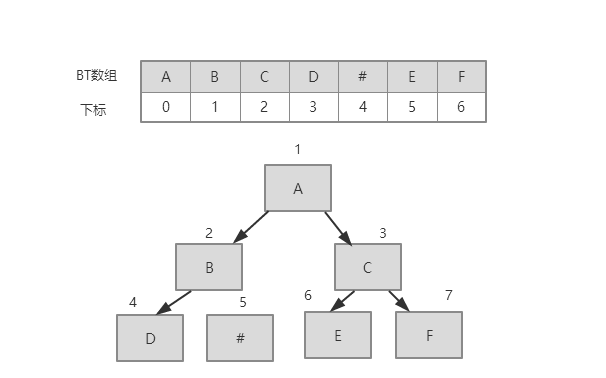
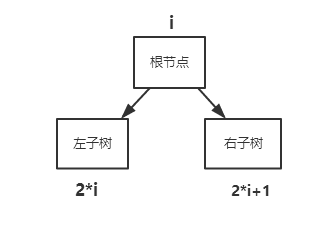
  根据根结点与两个孩子之间i的关系，可转换成二叉链建树。

void CreateBTree(BiTree& BT, string str, int i)
{
	int strlen;
	strlen = str.size();
	BT = new BiTNode;
	if (i > strlen - 1 || i < 1)
	{
		BT = NULL;
		return;
	}
	if (str[i] == '#')
	{
		BT = NULL;
		return;
	}
	BT->data = str[i];
	CreateBTree(BT->lchild, str, 2 * i);
	CreateBTree(BT->rchild, str, 2 * i + 1);
}

先序遍历：

BinTree CreatBinTree()
{
	char ch;
	BinTree T;
	scanf("%c", &ch);
	if (ch == '#')  T = NULL;
	else 
	{
		T = new TNode;
		T->Data = ch;
		T->Left = CreatBinTree();
		T->Right = CreatBinTree();			
	}

	return T;
}

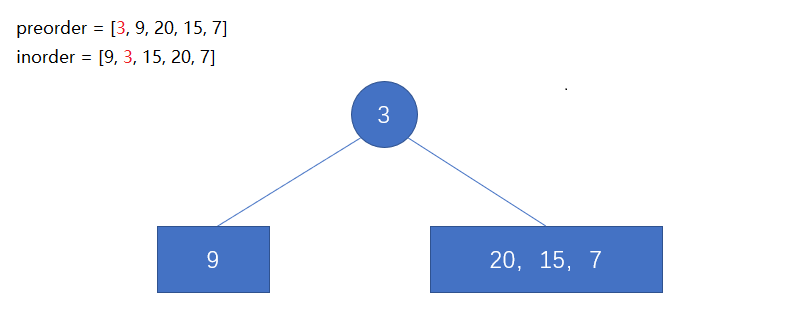
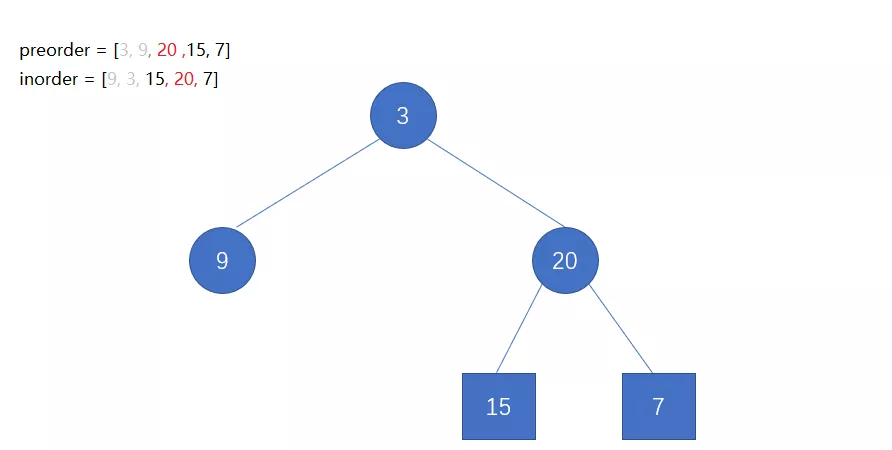
先序+中序序列：
前序遍历第一位数字一定是这个二叉树的根结点。中序遍历中，根结点讲序列分为了左右两个区间。左边的区间是左子树的结点集合，右边的区间是右子树的结点集合。

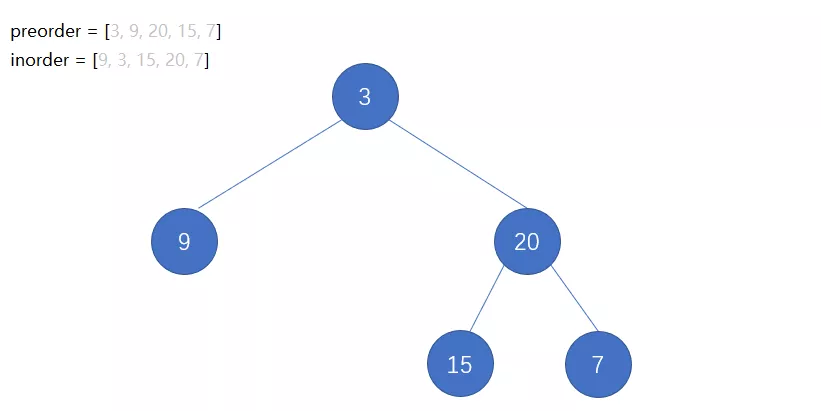
void CreateTree(BiTree& T, char* pre, char* infix, int n)
{
	int i;
	char* pi;
	if (n <= 0)
	{
		T = NULL;
		return;
	}
	T = new BiTNode;

	T->data = *pre;
	for (pi = infix; pi < infix + n; pi++)
	{
		if (*pi == T->data)
		{
			break;
		}
	}
	i = pi - infix;
	CreateTree(T->lchild, pre+1, infix, i);
	CreateTree(T->rchild, pre+i+1, pi + 1, n - i - 1);
}

中序+后序序列：
找到根结点（后序遍历的最后一位）在中序遍历中，找到根结点的位置，划分左右子树，递归构建二叉树。思路和先序+中序序列遍历一样。

void CreateTree(BiTree& T, int* post, int* infix, int n)
{
	int i;
	int* pi;
	if (n <= 0)
	{
		T = NULL;
		return;
	}
	T = new BiTNode;

	T->data = *(post + n - 1);
	for (pi = infix; pi < infix + n; pi++)
	{
		if (*pi == *(post + n - 1))
		{
			break;
		}
	}
	i = pi - infix;
	CreateTree(T->lchild, post, infix, i);
	CreateTree(T->rchild, post + i, pi + 1, n - i - 1);

}

• 二叉树的遍历：前序，中序，后序，层次
  前序：二叉树先序遍历的实现思想是：访问根节点；访问当前节点的左子树；若当前节点无左子树，则访问当前节点的右子树。

void PreOrderTraverse(BiTree T)
{
    if (T)
    {
        cout<<T->data<<" ";
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

中序：二叉树中序遍历的实现思想是：访问当前节点的左子树；访问根节点；访问当前节点的右子树。

void INOrderTraverse(BiTree T)
{
    if (T)
    {
        INOrderTraverse(T->lchild);
         cout<<T->data<<" ";
        INOrderTraverse(T->rchild);
    }
}

后序：二叉树后序遍历的实现思想是：从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。

void PostOrderTraverse(BiTree T)
{
    if (T) 
    {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        cout<<T->data<<" ";
    }
}

层次：层次遍历是从上到下、从左到右依次遍历每个结点。通过队列的应用，从根结点开始，将其左孩子和右孩子入队，然后根结点出队，重复次操作，直到队为空，出队顺序就是层次遍历的结果。

void LevelTravesal(BiTree T)
{
	queue<BiTree>qu;
	BiTree BT;
	int flag = 0;
	if (T == NULL)
	{
		cout << "NULL";
		return;
	}
	qu.push(T);
	while (!qu.empty())
	{
		BT = qu.front();
		if (flag == 0)
		{
			cout << BT->data;
			flag = 1;
		}
		else
		{
			cout << " " << BT->data;
		}
		qu.pop();
		if (BT->lchild != NULL)
		{
			qu.push(BT->lchild);
		}
		if (BT->rchild != NULL)
		{
			qu.push(BT->rchild);
		}
	}
}

• 二叉树的应用
  1．查找数据元素
  查找成功，返回该结点的指针；查找失败，返回空指针。

BiTree Search（BiTree bt，elemtype x）
{
    BiTree p;
    if (bt->data==x) return bt; /*查找成功返回*/
    if (bt->lchild!=NULL) return(Search(bt->lchild,x));
    if (bt->rchild!=NULL) return(Search(bt->rchild,x));
    return NULL; /*查找失败返回*/
}

2．统计出给定二叉树中叶子结点的数目

int CountLeaf2（BiTree bt）
{
    if (bt==NULL) return 0;
    if (bt->lchild==NULL && bt->rchild==NULL) return 1;
    return CountLeaf2(bt->lchild)+CountLeaf2(bt->rchild);
}

3．表达式运算
如图所示为表达式3x2+x-1/x+5的二叉树表示。树中的每个叶结点都是操作数，非叶结点都是运算符。

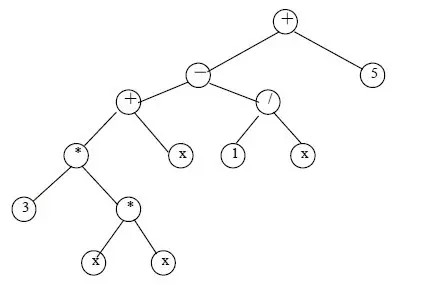
对该二叉树分别进行先序、中序和后序遍历，可以得到表达式的三种不同表示形式。
前缀表达式+-+3xxx/1x5
中缀表达式3xx+x-1/x+5
后缀表达式3xx**x+1x/-5+

• 树的结构、操作、遍历及应用
  树有双亲存储结构，孩子链存储结构，孩子兄弟链存储结构，我们常用的是最后一种。

typedef struct tnode
{
    ElemType data;
    struct tnode* son;
    struct tnode* brother;
}TSBNode;

树的遍历有先根遍历：若树不空，则先访问根结点，然后依次先根遍历各棵子树。后跟遍历：若树不空，则依次后根遍历各棵子树，然后访问根结点。层次遍历：若树不空，则自上而下，自左至右访问树中每个结点。具体代码和上面二叉树类似。
树的应用：可以求树的高度，建目录树。

• 线索二叉树
  二叉链存储结构时，每个结点都有两个指针，一共有2n个指针域，有效指针域为n-1个，空指针域有n+1个，可以利用空指针域指向该线性序列的前驱和后继指针，这称为线索。
  
  
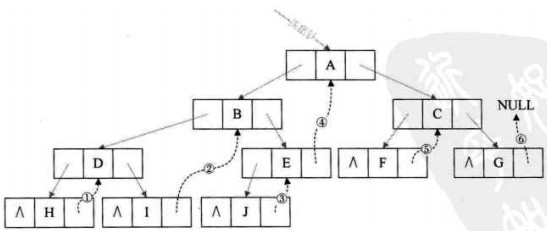
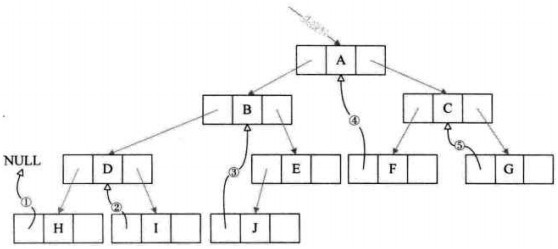
  线索二叉树：若结点有左子树，则其lchild域指向左孩子，否则指向直接前驱；若结点有右子树，则其rchild域指向右孩子，否则指向直接后继。
  为了避免混淆，再增加两个标志域LTag和RTag。若LTag=0，lchild域指向左孩子；若LTag=1，lchild域指向其前驱；若RTag=0，rchild域指向右孩子；若RTag=1，rchild域指向其后继。
  
  存储结构

typedef struct Node
 {
   ElemType data;
   int LTag,RTag;
   struct Node *lchild,*rchild; 
 }TBTNode;

• 哈夫曼树、并查集
  哈夫曼树
  带权路径长度：若有n个叶结点，每个叶结点的权值为Wk，从根结点到叶结点的长度为Lk，带权路径长度WPL=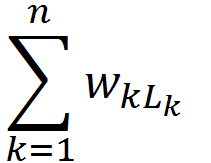
  哈夫曼树是最小带权路径长度的二叉树。哈夫曼树没有度为1的结点，如果有n个叶结点，则哈夫曼树的总结点数为2*n-1。
  构造哈夫曼树的原则：权值越大越靠近根结点，权值越小，离根结点越远。
  
  
  
  
  
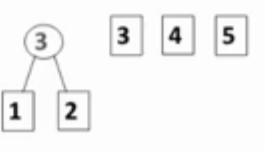
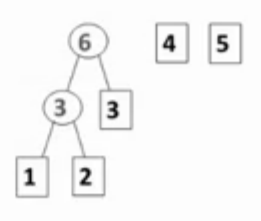
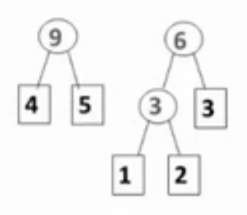
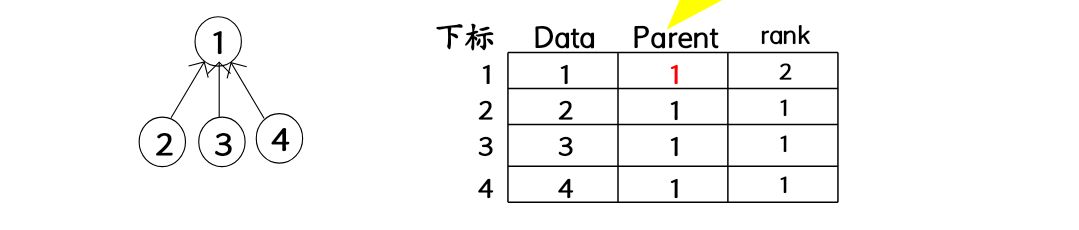
  并查集
  在并查集中，每个分离集合都算一棵树，并查集主要有集合查找，集合合并两个操作，采用顺序方法存储。

typedef struct node
{
     int data;
     int rank;
     int parent;
}UFSTree;

1.2.谈谈你对树的认识及学习体会。

本章主要学习了树的结构，属于非线性结构。线性结构是一对一关系，而树结构是一对多的关系。树结构有二叉树，线索二叉树和哈夫曼树，二叉树由一个根节点和左子树和右子树组成。线索二叉树是利用空余的指针指向结点前驱，而哈夫曼树利用带权路径解决最优问题。树结构的运算大部分都是递归运算，所以只有用好递归才能更加的熟悉树的操作。一般递归体分为左子树和右子树，递归口为结点为空或者其他条件。对树结构有了一定的学习后，发现代码调试时很困难，因为有些复杂了，但也为多对多关系打了基础。

2.阅读代码（0--5分）

2.1 题目及解题代码

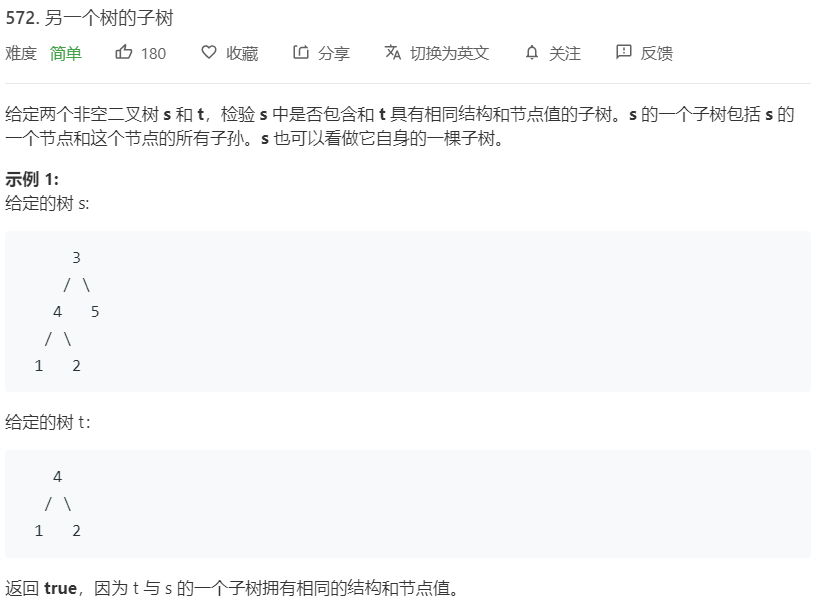
2.1.1 该题的设计思路

将树的每个节点t作为根，把相应子树和给定子树s进行比较，看是否相同。函数traverse(s,t)遍历树s，把每个节点都看成当前子树的根。equals(x,y) 函数检查两个子树是否相等。首先比较两个树的根是否相等，然后递归比较左子树和右子树是否都相等。

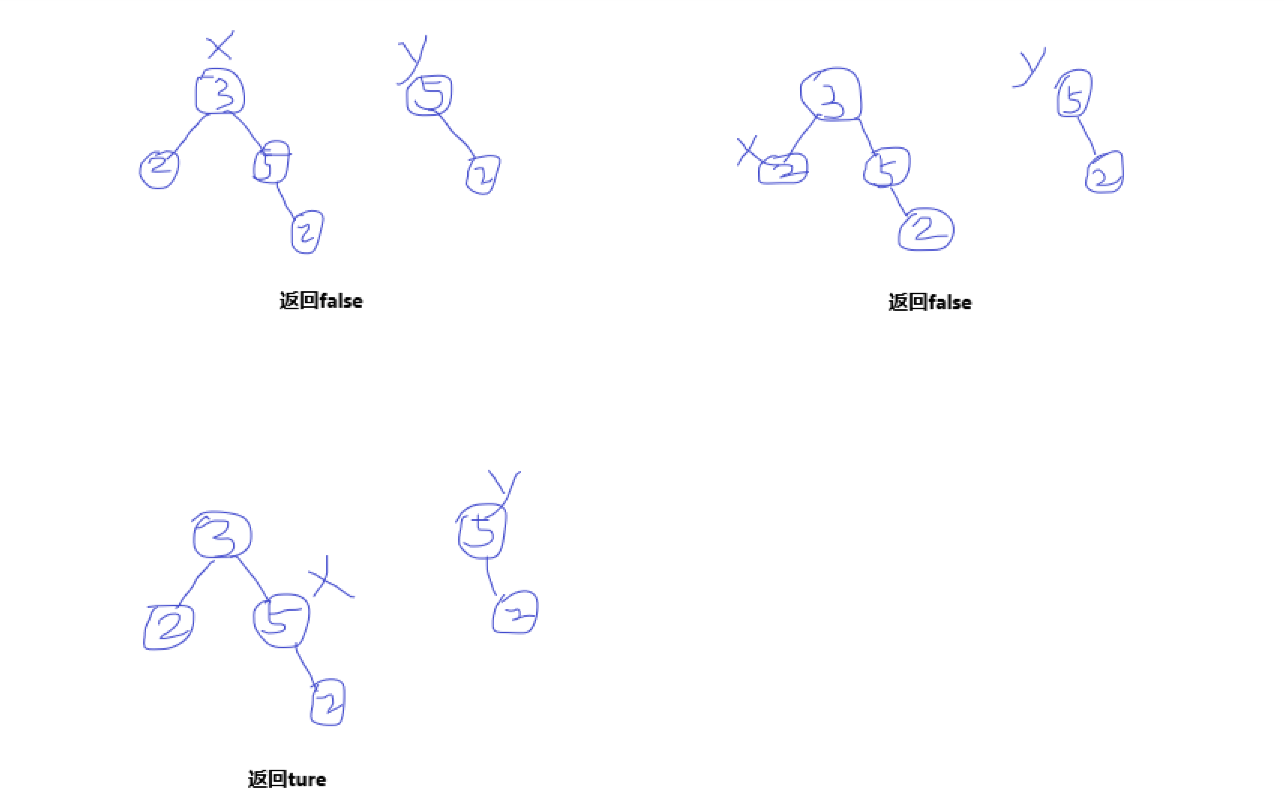
时间复杂度：O(mn)。
空间复杂度：O(n)。

2.1.2 该题的伪代码

    public boolean isSubtree(TreeNode s, TreeNode t) {
        返回调用的traverse(s, t)函数的值
    }
    private boolean traverse(TreeNode s, TreeNode t) {
        将每个节点视为当前正在考虑的子树的根，看是否为空，再调用equals()函数看是否相等
    }
    private boolean equals(TreeNode t1, TreeNode t2) {
        若相等 return true;
        否则 return false;
        递归判断左和右
    }
}

2.1.3 运行结果

2.1.4分析该题目解题优势及难点。

优势：时间复杂度和空间复杂度比较小
难点：在遍历给定的树s时，如何将每个节点视为当前正在考虑的子树的根，判断当前考虑的两个子树是否相等。

2.2 题目及解题代码

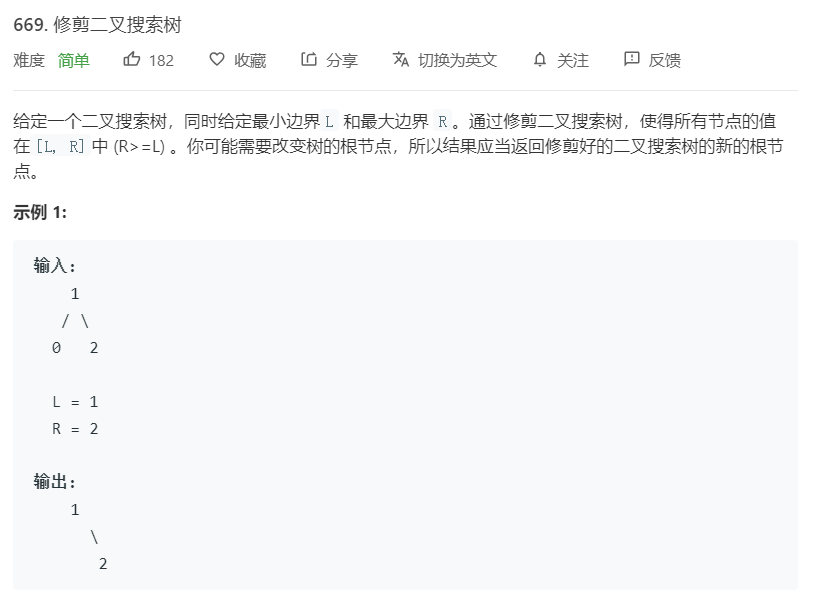
2.2.1 该题的设计思路

当 root.val > R，那么修剪后的二叉树会出现在节点的左边。当root.val < L时，那么修剪后的二叉树会出现在节点的右边。否则，修剪树的两边。
时间复杂度：O(N)。
空间复杂度：O(N)。

2.2.2 该题的伪代码

struct TreeNode* trimBST(struct TreeNode* root, int L, int R){
    root为空时，返回NULL
    若root->val < L
        返回trimBST(root->right, L, R);
    若R < root->val
        返回trimBST(root->left, L, R);
    接着找左孩子root->left = trimBST(root->left, L, R);
    接着找右孩子root->right = trimBST(root->right, L, R);
}

2.2.3 运行结果

2.2.4分析该题目解题优势及难点。

优势：利用递归的算法，减少了代码量，复杂度也相对较小。
难点：修减时如何替代前一个结点。

2.3 题目及解题代码

2.3.1 该题的设计思路

以树t1为基础，将t2合并到t1上。如果两棵树的根结点都不为空，则累加两个根结点的值；然后合并t1的左子树和t2的左子树；然后合并t1的右子树和t2的右子树；最后返回t1作为合并后的子树根结点。递归边界为：如果t1为空，则返回t2作为子树；如果t2为空，则返回t1作为子树。
空间复杂度和时间复杂度都为O(n)。

2.3.2 该题的伪代码

class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        若t1为空  return t2;
        若t2为空  return t1;
        两个根结点累加
        分别合并两棵树的左子树和右子树
    }
}

2.3.3 运行结果

2.3.4分析该题目解题优势及难点。

优势：不用新建一个树，而是在t1的基础上进行改动。
难点：根结点要怎么返回。

2.4 题目及解题代码

2.4.1 该题的设计思路

如果对一个节点的左孩子向下遍历最多有L个结点，右孩子向下遍历最多有R个结点，那么经过的节点数就为 L+R+1，记作dnode，则二叉树的直径就是dnode减一。函数depth(node）计算dnode。先求子树的深度L和R，则dnode为L+R+1，而全局变量ans记录dnode的最大值，最后返回的ans-1就是二叉树的直径。

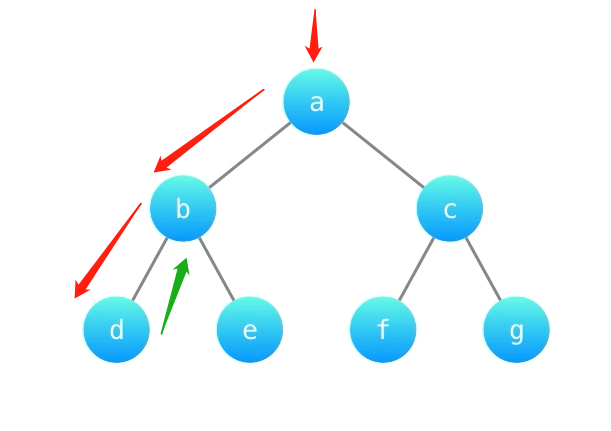
时间复杂度：O(N)，其中 N为二叉树的节点数。
空间复杂度：O(H)，其中 H为二叉树的高度。

2.4.2 该题的伪代码

class Solution {
    定义全局遍历ans;
    int depth(TreeNode* rt){
        若rt为空，返回0
        求左孩子为根的子树的深度
        求右孩子为根的子树的深度
        计算dnode
    }
};

2.4.3 运行结果

2.4.4分析该题目解题优势及难点。

优势：采用递归调用，把一个大问题，分成了若干个相似的小问题，即找以孩子为结点树的高度。
难点：如何来计算ans的值并更新。