0.PTA得分截图

1.本周学习总结(0-4分)
1.1 总结栈和队列内容
- 栈的存储结构及操作
1.顺序栈
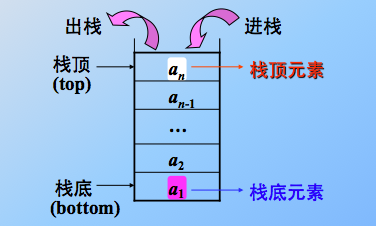
- 采用顺序存储结构可以模拟栈存储数据的特点,从而实现栈存储结构;利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针 top 指示栈顶元素在顺序栈中的位置,附设指针 front 指示栈底前一个的位置。 同样,应该采用可以动态增长存储容量的结构。且注意,如果栈已经空了,再继续出栈操作,则发生元素下溢,如果栈满了,再继续入栈操作,则发生元素上溢。栈底指针初始为空,说明栈不存在,栈顶指针 top 初始指向front,则说明栈空,元素入栈,则 top++,元素出栈,则top--。
- 入栈
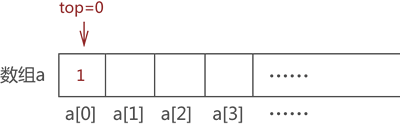
//元素elem进栈,a为数组,top值为当前栈的栈顶位置
int push(int* a,int top,int e)
{
a[++top]=e;
return top;
}
- 出栈
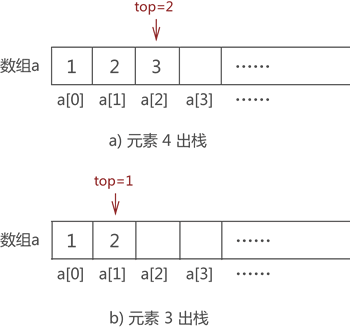
int pop(int * a,int top)
{
if (top==-1)
{
printf("空栈");
return -1;
}
printf("出栈元素:%d
",a[top]);
top--;
return top;
}
2.链栈

- 采用链式存储结构实现栈结构。
typedef struct SNode //链栈的结构体
{
int data;
struct SNode* next;
} SNode, * LinkStack;
Status InitStack(LinkStack& S) //初始化栈
{
S = NULL;
return OK;
}
bool StackEmpty(LinkStack S) //判断是否为空
{
if (!S)
return true;
return false;
}
Status Push(LinkStack& S, int e) //入栈
{
LinkStack p;
p = new SNode;
if (!p)
{
return OVERFLOW;
}
p->data = e;
p->next = S;
S = p;
return OK;
}
Status Pop(LinkStack& S, int& e) //出栈
{
LinkStack p;
if (!S)
return ERROR;
e = S->data;
p = S;
S = S->next;
delete p;
return OK;
}
- 栈的应用
基于栈结构对数据存取采用 "先进后出" 原则的特点,它可以用于实现很多功能。例如,我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A,然后关闭了页面 A 跳转到页面 B,随后又关闭页面 B 跳转到了页面 C。而此时,我们如果想重新回到页面 A,有两个选择:重新搜索找到页面 A;使用浏览器的"回退"功能。浏览器会先回退到页面 B,而后再回退到页面 A。浏览器 "回退" 功能的实现,底层使用的就是栈存储结构。当你关闭页面 A 时,浏览器会将页面 A 入栈;同样,当你关闭页面 B 时,浏览器也会将 B入栈。因此,当你执行回退操作时,才会首先看到的是页面 B,然后是页面 A,这是栈中数据依次出栈的效果。不仅如此,栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用到括号(小括号、中括号和大括号),括号的错误使用(通常是丢右括号)会导致程序编译错误,而很多开发工具中都有检测代码是否有编辑错误的功能,其中就包含检测代码中的括号匹配问题,此功能的底层实现使用的就是栈结构。 - 队列的存储结构及操作
- 队列的顺序存储结构又称为顺序队列,它也是利用一组地址连续的存储单元存放队列中的元素。由于队中元素的插入和删除限定在表的两端进行,因此设置队头指针和队尾指针,分别指示出当前的队首元素和队尾元素。在顺序队列中,为了降低运算的复杂度,元素入队时,只修改队尾指针;元素出对时,只修改队头指针。由于顺序队列的存储空间是提前设定的,因此队尾指针会有一个上限值,当队尾指针达到其上限时,就不能只通过修改队尾指针来实现新元素的入队操作了。此时,可将顺序队列假象成一个环状结构,称之为循环列表。
- 队列的链式存储也称为链队列。为了便于操作,可给链队列添加一个头结点,并令头指针指向头结点。队列为空的判断条件是头指针和尾指针的值相同,且均指向头结点。
1.顺序队列
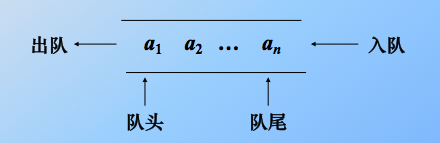
typedef struct {
int data[MAXQSIZE];
int front; //头指针
int rear; //尾指针
} Queue;
int EnQueue(SqQueue& Q, Person e)//加入队列
{
if (Q->rear + 1 == MAXQSIZE)
{
return 0;
}
else
{
Q->rear++;
Q->data[Q->rear] = e;
return 1;
}
}
int QueueEmpty(SqQueue& Q)//队列是否为空
{
return (Q->front == Q->rear);
}
int DeQueue(SqQueue& Q, Person& e)//出队列
{
if (Q->front == Q->rear)
return -1;
else
{
Q->front++;
e = Q->data[Q->front];
return 1;
}
}
2.循环队列
顺序队列的 “假溢出” 问题:队列的存储空间未满,却发生了溢出。很好理解,比如 rear 现在虽然指向了最后一个位置的下一位置,但是之前队头也删除了一些元素,那么队头指针经历若干次的 +1 之后,遗留下了很多空位置,但是顺序队列还在傻乎乎的以为再有元素入队,就溢出呢!肯定不合理。故循环队列诞生!
队空
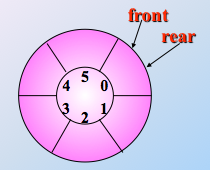
队满
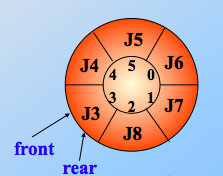
由于队空和队满的条件相同,为了解决这一问题,可以少用一个元素的空间,约定入队前测试尾指针在循环下加 1 后是否等于头指针,若相等则认为队满。
//求长度
int getLength(CirularQueue queue)
{
//这样把所以的情况都考虑到了
return (queue.rear - queue.front + MAX_SIZE) % MAX_SIZE;
}
void deleteQueue(CirularQueue *queue)//出队
{
if (queue->front == queue->rear)
{
puts("队列是空的!");
}
else
{
queue->front = (queue->front + 1) % MAX_SIZE;
}
}
void insertQueue(CirularQueue *queue, int e)//入队
{
if ((queue->rear + 1) % MAX_SIZE == queue->front) {
puts("循环队列是满的!");
}
else
{
queue->base[queue->rear] = e;
queue->rear = (queue->rear + 1) % MAX_SIZE;
}
}
3.链队
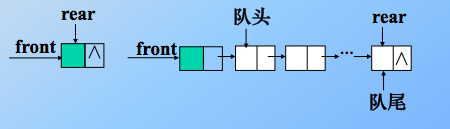
用链表表示的队列,限制仅在表头删除和表尾插入的单链表。一个链队列由一个头指针和一个尾指针唯一确定。(因为仅有头指针不便于在表尾做插入操作)。
typedef struct Node//链队结构体
{
int data;
struct Node *next;
} Node, *Queue;
bool isEmpty(LinkQueue queue)//判空
{
return queue.rear == queue.front ? true : false;
}
//入队,只在一端入队,另一端出队,同样入队不需要判满
void insertQueue(LinkQueue &queue, int temp)
{
Queue q = (Queue)malloc(sizeof(Node));
if (NULL == q)
{
exit(0);
}
q->data = temp;
q->next = NULL;
queue->rear->next = q;
queue->rear = q;
}
//出队,需要判空
void deleteQueue(LinkQueue &queue)
{
Queue q = NULL;
if (!queue.empty())
{
q = queue->front->next;
queue->front->next = q->next;
if (queue->rear == q)
{
queue->rear = queue->front;
}
free(q);
}
}
- 队列应用
队列数据结构常用于计算机操作系统。它们在多用户/多任务环境中尤为重要,在这种环境中,多个用户或任务可能同时请求同一资源。例如,打印由队列控制,因为一次只能打印一个文档。队列用于保存由系统用户提交的打印作业,而打印机则一次处理一个作业。通信软件也会使用队列来保存通过网络和拨号连接方式接收到的信息。有时,信息传输到系统的速度比它能处理的要快,因此在收到信息时会先将其放入队列中。
对于迷宫问题,我们可以使用队列来求解,假设当前点位为(x, y),在队列中的索引为front,遍历该位置的四个方位,如果方位可走则入队,并记录这个方位元素的前驱为front。如下图所示,当前点位上方的点位不可走,不入队;右方可走,入队;下方可走入队;左方可走入队;然后将front++,这时候当前点位变成(x, y+1),继续遍历它的四个方位,淘汰掉不可走的,可走的方位都会入队。这样一层一层向外扩展可走的点,所有可走的点位各个方向都会尝试,而且机会相等,直到找到出口为止,这个方法称为“广度搜索方法”。

1.2.谈谈你对栈和队列的认识及学习体会。
- 栈和队列是两种常用的数据结构,栈和队列是操作受限的线性表,栈和队列的数据元素具有单一的前驱和后继的线性关系;栈和队列又是两种重要的抽象数据类型。栈是限定在表尾进行插入和删除操作的线性表允许插入和删除的一端为栈顶,另一端为栈底,出栈元素只能是栈顶元素,后进先出,相邻元素具有前驱与后继关系。队列是只允许在一端进行插入操作,在另一端进行删除操作的线性表。允许插入的一端为队尾,允许删除的一端为队头,先进先出,相邻元素具有前驱与后继关系。栈可用于符号配对,走迷宫和计算后缀表达式等。栈可以分为顺序栈和链栈,运用于不同的情况。队列是先进先出,可在队头删除,也可以在队尾插入。队列也可分为顺序队和链队,在顺序队中,为了防止假溢出,又增加了循环队列。在C++中的stack、queue类模板中,已经有写好的一些操作的基本函数,可以直接使用,比较方便。通过对栈和队列的学习,感觉应用十分广泛,可以很奇妙的解决很多问题,非常好用。
2.PTA实验作业(0-2分)
2.1.题目1:7-3 jmu-ds-符号配对 (15分)
2.1.1代码截图(注意,截图,截图,截图。不要粘贴博客上。)
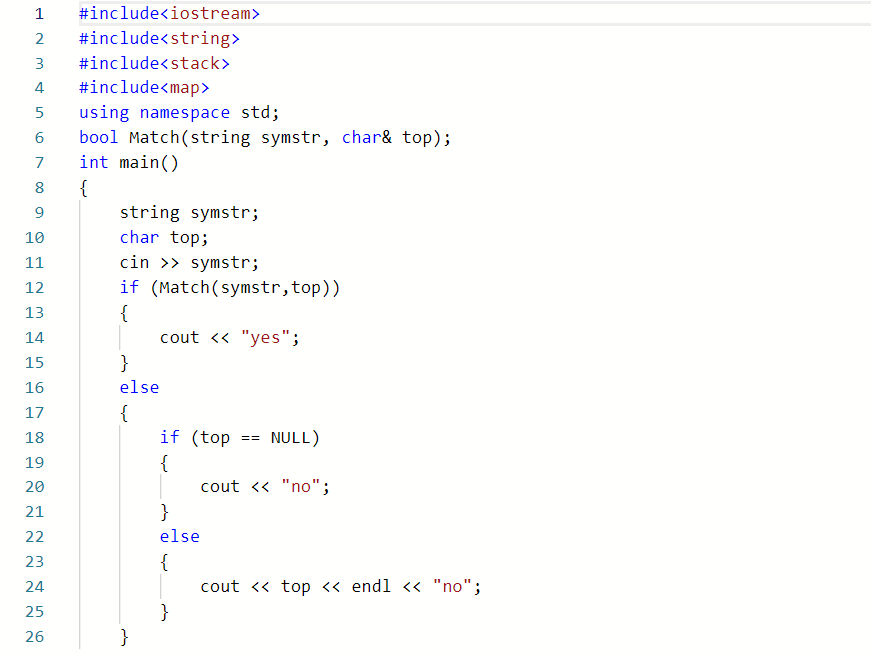
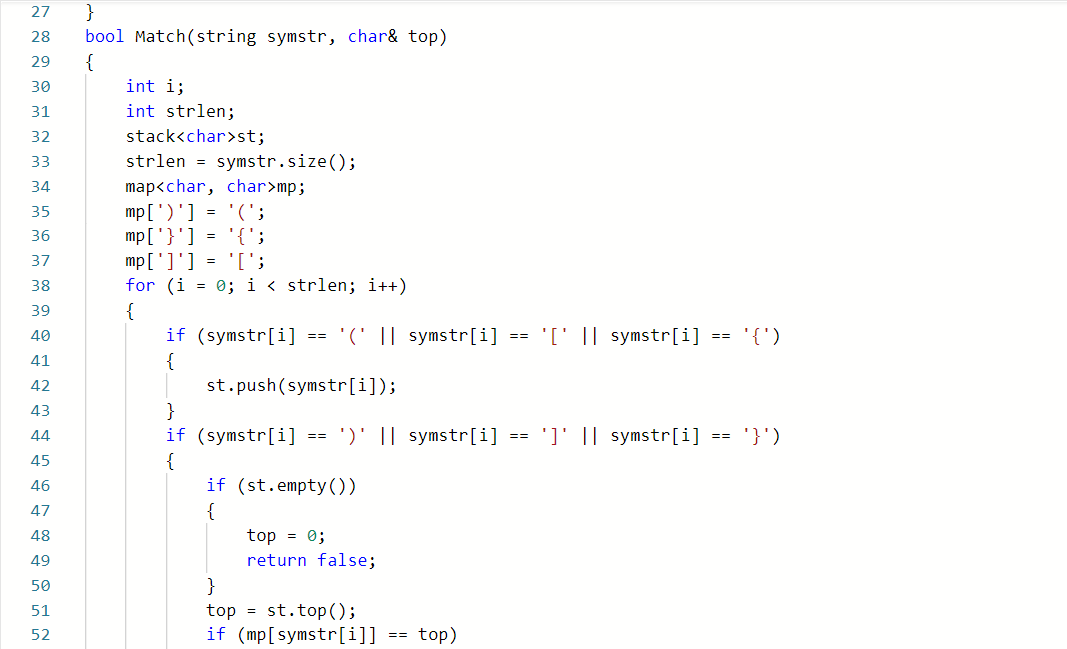

2.1.2本题PTA提交列表说明。##

因为是老师讲过的代码,有印象。第一次错,是符合不匹配且栈空时错误,多输出了一个换行。解决办法是,在返回时,考虑top为空的情况单独输出。
2.2.题目1:7-6 jmu-报数游戏 (15分)
2.2.1代码截图(注意,截图,截图,截图。不要粘贴博客上。)
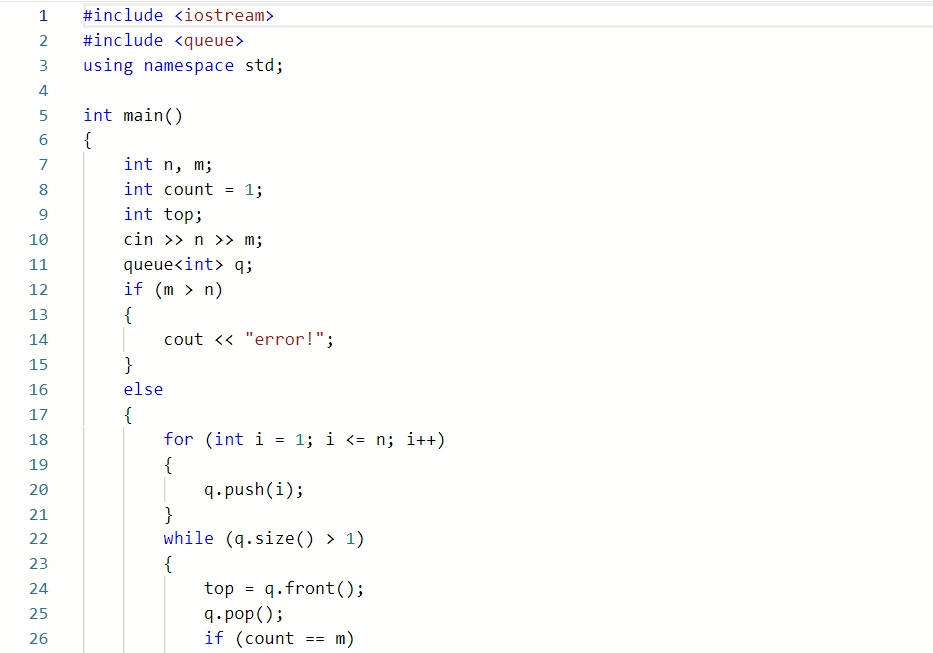

2.2.2本题PTA提交列表说明。

刚开始部分正确是因为少了一种情况。解决方法是把n<m的这种情况写了一个条件。
3.阅读代码(0--4分)
3.1 题目及解题代码
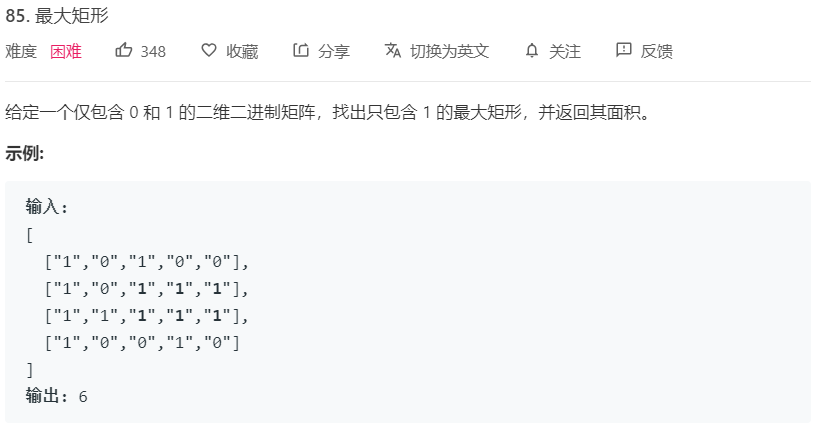
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if(!matrix.size()) return 0;
vector<int> dp(matrix[0].size(),0);
int maxArea = 0;
for(int i=0;i<matrix.size();++i)
{
for(int j=0;j<matrix[0].size();++j)
{
dp[j] = (matrix[i][j]=='1') ? dp[j]+1 : 0;
}
maxArea=max(maxArea,maxRectangleArea(dp));
}
return maxArea;
}
private:
int maxRectangleArea(vector<int> &nums)
{
stack<int> s;
nums.push_back(0);
int maxArea = 0;
for(int i=0;i<nums.size();++i)
{
while(!s.empty() && nums[i]<=nums[s.top()])
{
int top = s.top();s.pop();
maxArea = max(maxArea,nums[top]*(s.empty()?i:i-s.top()-1));
}
s.push(i);
}
nums.pop_back();
return maxArea;
}
};
3.1.1 该题的设计思路
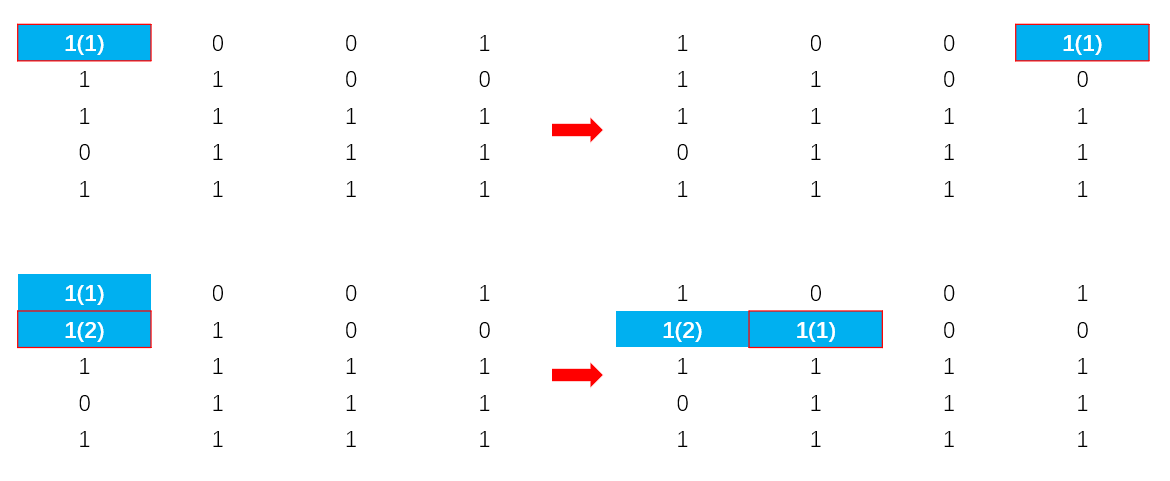
红色边框勾出矩阵遍历过程,表格中数字旁边的括号标出当前dp[i]的值,蓝色填充区域表示矩阵中以当前结点为右下角,能完全包含该结点高度的矩形最大面积。
用动态规划的思想,从上层得到下一层能建立的柱体的最大高度,然后在每一层借用单调栈求出以该柱体为高的最大矩形面积。
时间复杂度为O(MN),空间复杂度为O(M),M,N分别为矩阵长,宽。
3.1.2 该题的伪代码
int maximalRectangle(vector<vector<char>>& matrix)
{
判断是否为空
记录以某一层为底,与之前的所有上层可以形成的连续高度
int maxArea = 0;
for(遍历)
循环中调用amxRectangleArea()算法,
用于找到在一层中结点matrix[i][j]完整包含dp[j]高度的最大宽度
面积就等于找到的长 * 宽
end for
}
int maxRectangleArea(vector<int> &nums)//用于找到nums中完整包含当前高度的最长宽度
{
定义栈
设置一个哨兵,让nums遍历到最后时,获得的柱体高度可让单调栈前面的所有元素出栈
int maxArea = 0;
for(遍历)
while(不为空且nums[i]小于等于nums[s.top()])
取栈顶并出栈
得到最大区域
end while
入栈
end for
}
};
3.1.3 运行结果


3.1.4分析该题目解题优势及难点。
- 本题解题优势是利用了一个哨兵和动态规划的思想,利用单调栈的解题思路。难点在于如何找到矩形。
3.2 题目及解题代码

class Solution {
public:
enum { MAXN = 80001 };
int mark[MAXN] = {0};
int minIncrementForUnique(vector<int>& A) {
if(A.size() <= 0){
return 0;
}
int maxValue = 0;
for(size_t i = 0, n = A.size(); i < n; ++i){
++mark[A[i]];
maxValue = max(maxValue, A[i]);
}
int ans = 0;
maxValue <<= 1;
for(int i = 0; i <= maxValue; ++i){
if(mark[i] > 1){
ans += mark[i] - 1;
mark[i+1] += mark[i]-1;
mark[i] = 1;
}
}
return ans;
}
};
3.2.1 该题的设计思路
- 如果一个数 x 出现了 c 次,当 c > 1 时,必然要对 c-1 个 x 执行 move 操作,以使得 x 在整个数组中具有唯一性。
那么对于 c-1 个 x+1 按照上述步骤继续处理,直到数组中的元素两两不相等:
当 c-1 > 1 时,必然对 c-2 个 x+1 执行move操作,以使得 x+1 在整个数组中具有唯一性。
因为给出的元素不会超过 40000,所以操作之后的最大元素不会超过80000。
设 maxValue 为操作之后的最大值。鉴于 maxValue 并不大我们可以使用hash数组来统计数组中每个元素的格数。之后我们遍历该数组并记录move操作的次数即可。
以 [3,2,1,2,1,5] 为例, 首先对次数进行统计,如下图所示:
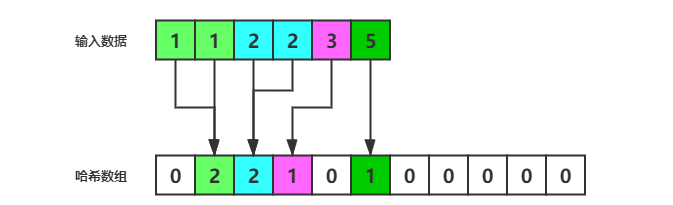
统计完成后,遍历得到的哈希数组以计算操作次数,如下图所示:
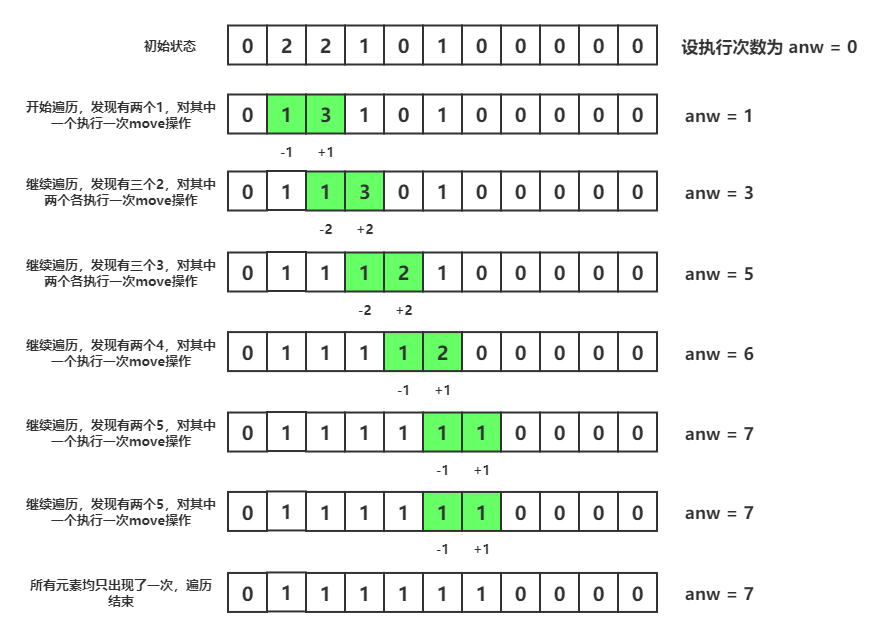
时间复杂度为O(n),空间复杂度为O(n)。
3.2.2 该题的伪代码
定义一个很大的mark数组
int minIncrementForUnique(vector<int>& A)
{
判断是否为空
int maxValue = 0;
for(遍历)
++mark[A[i]];
maxValue取较大数
end for
int ans = 0;
maxValue <<= 1;
for(遍历)
if(mark[i] 大于 1)
统计ans
下一个位置加上当前位置的数再减一
mark[i] 等于1
end if
end for
}
3.2.3 运行结果



3.2.4分析该题目解题优势及难点。
- 虽然 A[i] 的范围为 [0, 40000),但我们有可能会将数据递增到 40000 的两倍 80000。这是因为在最坏情况下,数组 A 中有 40000 个 40000,这样要使得数组值唯一,需要将其递增为 [40000, 40001, ..., 79999],因此用来统计的数组需要开到 80000。优势在于减少了时间复杂度,但增加了空间复杂度。难点在于用哈希数组的统计不好理解,看了好长时间才明白一点。