点多边形测试

什么叫点多边形检测

测试一个点是否在给定的多边形内部，边缘或者外部

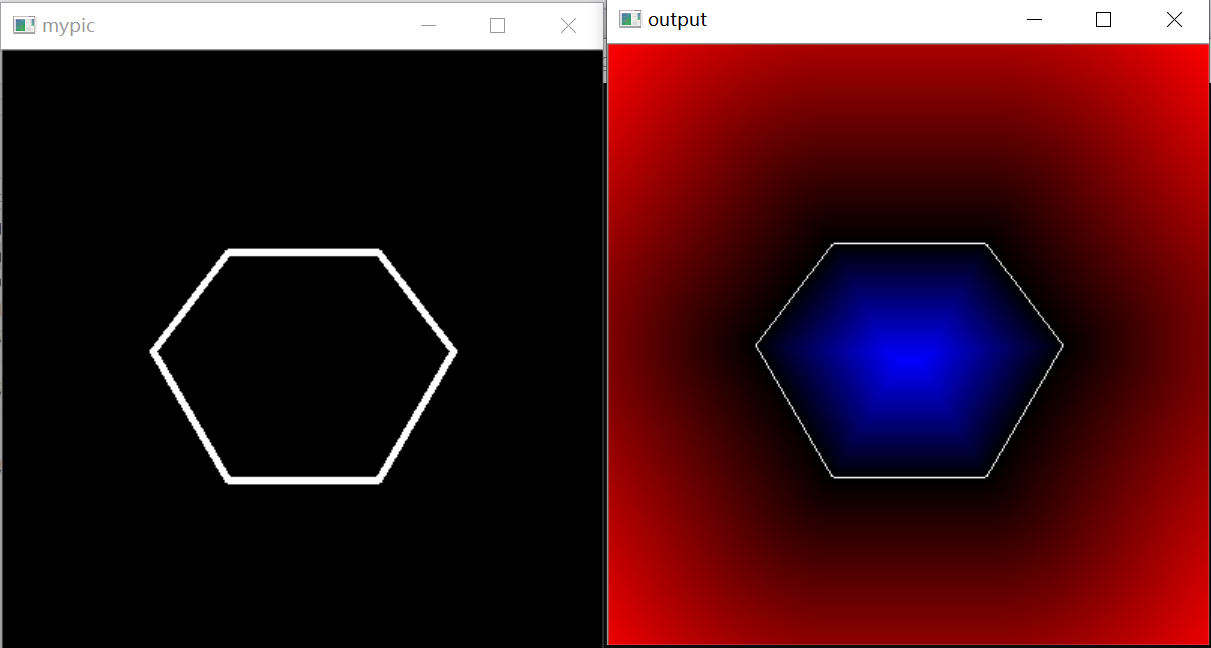
根据所有点到多边形中心距离可以生成一幅图像（测试图）

cv::pointPolygonTest

InputArray contour 输入的轮廓

Point2f pt 测试点

bool measureDist 是否返回距离值，否的话返回三个值1在内部，0在边界，-1在外面

步骤

构建一张400x400八通道的图像

画一个闭合六边形

发现轮廓

对图像中所有的点做点多边形测试，得到距离，归一化后显示

#include<iostream>
#include"pch.h"
#include<opencv2/opencv.hpp>
#include<math.h>

using namespace std;
using namespace cv;

int main(int argc, char**argv)
{
    const int r = 100; 
    Mat src = Mat::zeros(r * 4, r * 4, CV_8UC1);
    vector<Point2f> vert(6);
    vert[0] = Point(3 * r / 2, static_cast<int>(1.34*r));
    vert[1] = Point(1 * r, 2 * r);
    vert[2] = Point(3 * r / 2, static_cast<int>(2.866*r));
    vert[3] = Point(5 * r / 2, static_cast<int>(2.866*r));
    vert[4] = Point(3 * r, 2 * r);
    vert[5] = Point(5 * r / 2, static_cast<int>(1.34*r));

    for (int i = 0; i < 6; ++i)
    {
        line(src, vert[i], vert[(i + 1) % 6], Scalar(255), 3, 8, 0);
    }

    imshow("mypic", src);

    vector<vector<Point>> contours;
    vector<Vec4i> hierachy;

    Mat csrc;
    src.copyTo(csrc);
    findContours(csrc, contours, hierachy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0));

    Mat raw_dist = Mat::zeros(csrc.size(), CV_32FC1);
    for (int row = 0; row < raw_dist.rows; ++row)
        for (int col = 0; col < raw_dist.cols; ++col)
        {
            double dist = pointPolygonTest(contours[0], Point2f(static_cast<float>(col), static_cast<float>(row)), true);
            raw_dist.at<float>(row, col) = static_cast<float>(dist);//用距离大小替代像素值
        }

    double minValue, maxValue;
    minMaxLoc(raw_dist, &minValue, &maxValue, 0, 0, Mat());
    Mat drawImg = Mat::zeros(src.size(), CV_8UC3);
    for (int row = 0; row < drawImg.rows; ++row)
        for (int col = 0; col < drawImg.cols; ++col)
        {
            float dist = raw_dist.at<float>(row, col);
            if (dist > 0)
            {
                drawImg.at<Vec3b>(row, col)[0] = (uchar)(abs(dist / maxValue) * 255);
            }
            else if (dist < 0)
            {
                drawImg.at<Vec3b>(row, col)[2] = (uchar)(abs(dist / minValue) * 255);
            }
            else
            {
                drawImg.at<Vec3b>(row, col)[0] = (uchar)(abs(255-dist));
                drawImg.at<Vec3b>(row, col)[1] = (uchar)(abs(255 - dist));
                drawImg.at<Vec3b>(row, col)[2] = (uchar)(abs(255 - dist));
            }
        }

    imshow("output", drawImg);
    waitKey(0);
    return 0;
}