72. 编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符
示例 1:

输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:

输入: word1 = "intention", word2 = "execution"
输出: 5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

动态规划：
dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数

所以，

当 word1[i] == word2[j]，dp[i][j] = dp[i-1][j-1]；

当 word1[i] != word2[j]，dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1

其中，dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。

注意，针对第一行，第一列要单独考虑，我们引入 '' 下图所示：

 

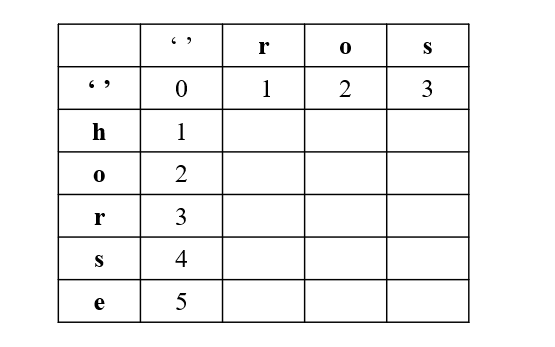
第一行，是 word1 为空变成 word2 最少步数，就是插入操作

第一列，是 word2 为空，需要的最少步数，就是删除操作

class Solution {
public:
    int minDistance(string word1, string word2) {
        if(word1.size()==0)
            return word2.size();
        if(word2.size()==0)
            return word1.size();
        vector<vector<int>>vec_vec(word1.size()+1,vector<int>(word2.size()+1,0));
        for(int i=1;i<=word2.size();i++)
        {
            vec_vec[0][i]=i;
        }
        for(int i=1;i<=word1.size();i++)
        {
            vec_vec[i][0]=i;
        }

        for(int i=1;i<=word1.size();i++)
        {
            for(int j=1;j<=word2.size();j++)
            {
                if(word1[i-1]==word2[j-1])
                {
                    vec_vec[i][j]=vec_vec[i-1][j-1];
                }
                else
                {
                    vec_vec[i][j]=min(min(vec_vec[i-1][j],vec_vec[i-1][j-1]),vec_vec[i][j-1])+1;
                }
            }
        }
        return vec_vec[word1.size()][word2.size()];
    }
};

 另外一种递归的写法，从上向下，记得要加一个二维数组保存已经计算过的结果，否则会超时

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> vec_vec(word1.size(),vector<int>(word2.size(),0));
        return dp(word1.size()-1,word2.size()-1,word1,word2,vec_vec);
    }

    int dp(int i,int j,string word1, string word2,vector<vector<int>>&vec)
    {
        //一个小于0，说明另外一个剩下的都需要删除
        if(i<0)
        {
            return j+1;
        }
        if(j<0)
        {
            return i+1;
        }
        if(vec[i][j]!=0)
        {
            return vec[i][j];
        }
        if(word1[i]==word2[j])
        {
            vec[i][j]= dp(i-1,j-1,word1,word2,vec);
        }
        else
        {
            vec[i][j]=min(min(dp(i-1,j-1,word1,word2,vec),dp(i-1,j,word1,word2,vec)),dp(i,j-1,word1,word2,vec))+1;
        }
        return vec[i][j];
    }
};