DeepWalk
Background
使用机器学习的算法解决问题需要有大量的信息,但是现实世界中的网络中的信息往往比较少,这就导致传统机器学习算法不能在网络中广泛使用。
(Ps: 传统机器学习分类问题是学习一种假设,将样本的属性映射到样本的类标签,但是现实网络中的结点属性信息往往比较少,所以传统机器学习方法不适用与网络。)
Introduce
deepWalk是网络表征学习的比较基本的算法,用于学习网络中顶点的向量表示(即学习图的结构特征即属性,并且属性个数为向量的维数),使得能够应用传统机器学习算法解决相关的问题。
Algorithm Theory
-
input:邻接表
每行代表一个顶点的所有边
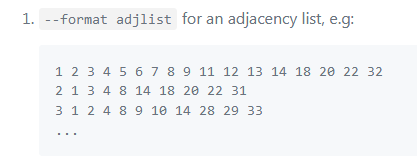
-
output:
第一行为结点个数和向量维数,后面每行为一个结点的向量表示,第一列为nodeId**
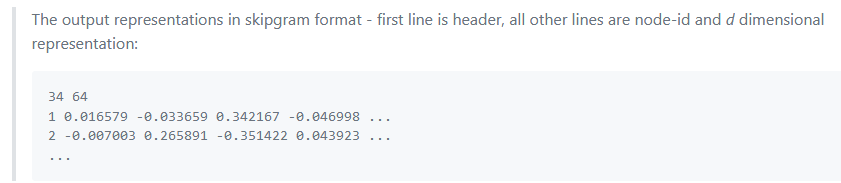
-
innovation:
借助语言建模word2vec中的一个模型,skip-gram来学习结点的向量表示。将网络中的结点模拟为语言模型中的单词,而结点的序列(可由随机游走得到)模拟为语言中的句子,作为skip-gram的输入。
-
feasibility:
以上假设的可行性证明,当图中结点的度遵循幂律分布(通俗讲即度数大的节点比较少,度数小的节点比较多)时,短随机游走中顶点出现的频率也将遵循幂律分布(即出现频率低的结点多),又因为自然语言中单词出现的频率遵循类似的分布,因此以上假设可行。(Ps: 为证明有效性,作者针对YouTube的社交网络与Wikipedia的文章进行了研究,比较了在短的随机游走中节点出现的频度与文章中单词的频度进行了比较,可以得出二者基本上类似。(幂率分布))
-
process:
随机游走+skip-gram 语言模型

通过随机游走得到短的结点序列,通过skip-gram更新结点向量表示。 -
Random Walk
Random Walk从截断的随机游走序列中得到网络的局部信息,并以此来学习结点的向量表示。
deepwalk中的实现是完全随机的,根据Random Walk的不同,后面又衍生出了node2vec算法,解决了deepwalk定义的结点相似度不能很好反映原网络结构的问题。
-
skip-gram 语言模型
skip-gram 是使用单词来预测上下文的一个模型,通过最大化窗口内单词之间的共现概率来学习向量表示,在这里扩展之后便是使用结点来预测上下文,并且不考虑句子中结点出现的顺序,具有相同上下文的结点的表示相似。(Ps:两个node同时出现在一个序列中的频率越高,两个node的相似度越高。)
结点相似性度量: 上下文的相似程度(LINE中的二阶相似度)
共现概率根据独立性假设可以转化为各条件概率之积即
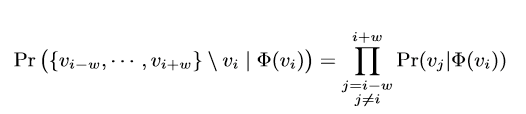
对序列中的每个顶点,计算条件概率,即该结点出现的情况下序列中其他结点出现的概率的log值并借助随机梯度下降算法更新该结点的向量表示。

Φ(vj)为当前结点的向量表示。Hierarchical Softmax用于分解并加快计算第三行的条件概率。
Advantage
- 并行性:同时进行多个随机游走。
- 适应性:当图变化后,不需要全局重新计算,可迭代更新,因此可以为大规模、稀疏的图创建有意义的表示。
Experiment
本次实验在人工网络上进行(平均度为20,最大度为50,一个社区小包含结点数minc为10,最大maxc为100),deepwalk参数为默认值,训练向量维数为64。分别在mu(混合度)为0.1,0.2,0.3,0.4,0.5,0.6,并且节点规模N为2k,4k,6k,8k,10k上进行。使用sklearn库的K-means进行聚类,K进行人工调整在实际值,重复每个实验10次并且计算每个实验的平均NMI值。
| NMI | N=2k | N=4k | N=6k | N=8k | N=10k |
|---|---|---|---|---|---|
| u=0.1 | 0.955741 | 0.965896 | 0.973577 | 0.973319 | 0.969941 |
| u=0.2 | 0.958258 | 0.958192 | 0.960152 | 0.955094 | 0.957447 |
| u=0.3 | 0.955079 | 0.941854 | 0.933403 | 0.929904 | 0.932717 |
| u=0.4 | 0.953002 | 0.924042 | 0.908161 | 0.916834 | 0.913081 |
| u=0.5 | 0.949694 | 0.895752 | 0.876676 | 0.878265 | 0.876310 |
| u=0.6 | 0.897372 | 0.872618 | 0.852643 | 0.838807 | 0.835484 |
存在问题:
聚类参数k的确定问题对实验的影响很大。
本实验未探究deepwalk参数即训练的向量维数,随机游走长度,迭代次数,skip-gram窗口大小对聚类精度的影响。