马拉车模板

马拉车算法介绍

马拉车算法：得到以i为中心的最长子串的半径、找最长子串、找有多少个子串。

详解

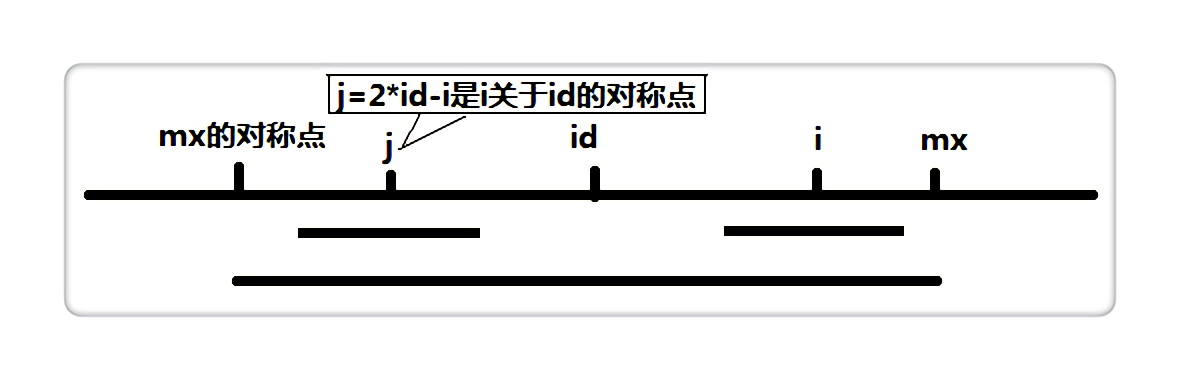
用mx和id两个中间量来加快回文串匹配的过程，并且更新mx的最大值。mx为最大右边界，id为其中心，当i<mx时可以缩短求解过程

例题

模板
1482: 简单的回文串计数

代码

char a[12000000];
int R[23000000];
int manacher()
{
	string s="$#";
	int l1=strlen(a);
	for(int i=0;i<l1;i++)
	{
		s+=a[i];
		s+='#';
	}
	int len=2*l1+1;
	int mx=0,id=0;
	int max_len=0;

	for(int i=1;i<len;i++)
	{
		
		if(i<mx)
		{
			R[i]=min(R[2*id-i],mx-i);
		}
		else
		R[i]=1;
		while(s[i-R[i]]==s[i+R[i]])
		{
			R[i]++;
		}
		if(mx<i+R[i])
		{
			id=i;
			mx=i+R[i];
		}
		max_len=max(max_len,R[i]-1);
	}
	return max_len;
}
main(void)
{
	scanf("%s",&a);
	cout<<manacher();
}

简单回文计数

#include<bits/stdc++.h>
#define int long long
using namespace std;
char a[3000004];
int ans1[3000004];
int cha1[3000004];
int cha2[3000004];
int ans[3000004];
int l,n,m;
void manacher()
{
 
	string res; 
    res="$#";
    for(int i=0;i<n;++i)
    {
        res+=a[i];
        res+="#";
    }
	 
    vector<int> P(l,0);
    int mi=0,right=0;   
    int maxLen=0,maxPoint=0; 
    for(int i=1;i<l;++i)
    {
     
        if(right>i)
            P[i]=min(P[2*mi-i],right-i);
        else
            P[i]=1;
  
        while(res[i+P[i]]==res[i-P[i]])
            ++P[i];
        
        if(right<i+P[i])  
        {
            right=i+P[i];
            mi=i;
        }

        if(maxLen<P[i])   
        {
            maxLen=P[i];
            maxPoint=i;
        }
       	cha2[i-P[i]+1]++;
		cha2[i+1]-=2;
		cha2[i+P[i]+1]++;
    }
     	
}
main(void)
{
	
	scanf("%lld%lld",&n,&m);
	l=2*n+2;
	for(int i=0;i<m;i++)
	{
		for(int k=0;k<=l;k++)
		{
			cha1[k]=0;
			cha2[k]=0;
			ans1[k]=0;
		}
		getchar();
		for(int j=0;j<n;j++)
		{
			a[j]=getchar();
			
		}
		manacher();
		for(int j=1;j<l;j++)
		{
			cha1[j]=cha1[j-1]+cha2[j]; 
			ans1[j]=ans1[j-1]+cha1[j];
			ans[j]+=ans1[j];
		}
	
		
	}
	for(int i=2;i<l;i=i+2)
    {
    	 if(i==2)
    	 {
    	   printf("%lld",ans[i]/2);
    	 }
    	 else
    	 {
    	 	printf(" %lld",ans[i]/2);
    	 }
	}
}