Python基础-递归函数

 1. 初始递归

1.1 递归的定义

　　在一个函数的再调用里调用这个函数本身，这种使用函数的方法叫做递归。

1.2 递归的最大深度--997

　　归函数如果不受到外力的阻止会一直执行下去。但是我们之前已经说过关于函数调用的问题，每一次函数调用都会产生一个属于它自己的名称空间，如果一直调用下去，就会造成名称空间占用太多内存的问题，于是python为了杜绝此类现象，强制的将递归层数控制在了997

验证代码--测试最大递归深度

def foo(n):
    print(n)
    n += 1
    foo(n)
foo(1)

　　由此我们可以看出，未报错之前能看到的最大数字就是997.当然了，997是python为了我们程序的内存优化所设定的一个默认值，我们当然还可以通过一些手段去修改它：

import sys
print(sys.setrecursionlimit(100000))

　　我们可以通过这种方式来修改递归的最大深度，刚刚我们将python允许的递归深度设置为了10w，至于实际可以达到的深度就取决于计算机的性能了。不过我们还是不推荐修改这个默认的递归深度，因为如果用997层递归都没有解决的问题要么是不适合使用递归来解决要么是你代码写的太烂了

2. 递归函数的使用

2.1 递归函数与三级菜单

menu = {
    '北京': {
        '海淀': {
            '五道口': {
                'soho': {},
                '网易': {},
                'google': {}
            },
            '中关村': {
                '爱奇艺': {},
                '汽车之家': {},
                'youku': {},
            },
            '上地': {
                '百度': {},
            },
        },
        '昌平': {
            '沙河': {
                '老男孩': {},
                '北航': {},
            },
            '天通苑': {},
            '回龙观': {},
        },
        '朝阳': {},
        '东城': {},
    },
    '上海': {
        '闵行': {
            "人民广场": {
                '炸鸡店': {}
            }
        },
        '闸北': {
            '火车战': {
                '携程': {}
            }
        },
        '浦东': {},
    },
    '山东': {},
}

menu

2.2 递归函数与二分查找法

有如下列表，让你从这个列表中找到66的位置，你要怎么做？

 l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

l.index(66).. soeasy的方法。现在如果没有了index方法，你改怎么实现呢？

方法一：

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

i = 0
for i in l:
    if i == 66:
        print(i)
    i+=1

这种方法是用for循环，去遍历这个列表，直到找到66的位置。假如这个列表非常的长，那么使用这种方法，效率就太低了。

二分查找算法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

 观察这个列表会发现，这是一个从小到大排列的有序列表

假如我要找的数与列表中间的数相比，如果比较大，那么就在列表的后半部找，如果比较小，就在列表的前半部找：

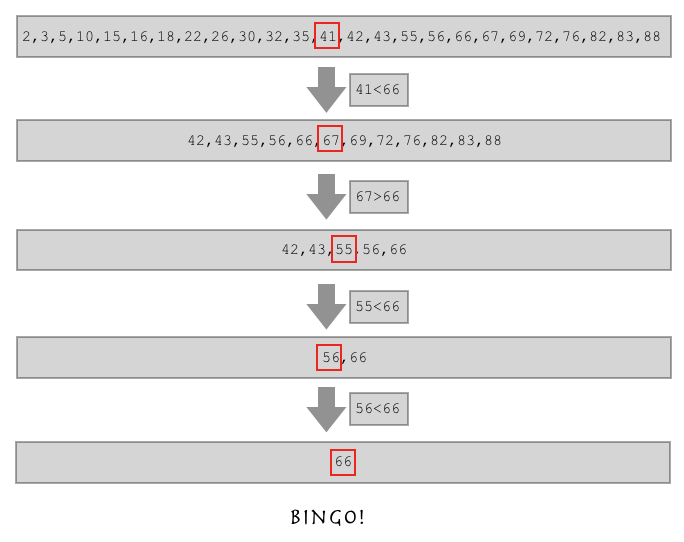
这就是二分查找算法

缺陷版：

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

def cal(num = 66):
    global l
    length = len(l)
    mid = (length-1)//2
    if num > l[mid]:
        l = l[mid+1:]
        cal(num)
    elif num < l[mid]:
        l = l[:mid]
        cal(num)
    else:
        print('找到了',l[mid],'的位置是',mid)

cal(66)

 这种方法可以找到66，但是索引的位置改变了。因为我们在查找的过程中对列表l做了切片处理。

而且查找一个不存在的数字会报错。

优化版：

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

def cal(num = 66):
    global l
    length = len(l)
    mid = (length-1)//2
    if l:
        if num > l[mid]:
            l = l[mid+1:]
            cal(num)
        elif num < l[mid]:
            l = l[:mid]
            cal(num)
        elif num == l[mid]:
            print('找到了',l[mid],'的位置是',mid)
    else:
        print('没找到')

cal(65)

接下来解决索引改变的问题： 

定义start 和 end两个位置点，并在接下来的过程中，不停的缩小间距，达到快速定位的结果

l = [2, 3, 5, 10, 15, 16, 18, 22, 26, 30, 32, 35, 41, 42, 43, 55, 56, 66, 67, 69, 72, 76, 82, 83, 88]

def cal(num=66, start=0, end=None):   ## 在参数定义阶段 不能给end赋值，否则每次递归调用的时候end都会获取到这个值
    end = len(l) - 1 if end is None else end   ## 
    if start <= end:
        mid = (end - start) // 2 + start
        if l[mid] > num:
            return cal(num,start,mid-1)   # 每次改变文件的位置
        elif l[mid] < num:
            return cal(num,mid+1,end)
        else:
            return mid
    else:                ## 解决对象不存在的问题
        return None

print(cal())