论文名称:用于异步时间序列的自回归卷积神经网络
论文摘要:
金融时间序列通常包含多个维度,不同维度数据的采样频率也不一致,例如螺纹钢研究员通常关心螺纹钢的因素有日频更新的现货螺纹钢价格,周频更新的螺纹钢价格,高炉开工率和线螺采购量,而月频更新的则有商品房销售面积等,如果其中某些可观测因子发生变化,投资则对未来螺纹钢的预期也应发生变化,但是如何处理这些不同频率的数据是量化模型的一个难题,一种比较简单的方法是降低数据的采样频率,例如把日频数据统一为周频,再基于周频进行预测,但这种方法的缺点也很明显,期货本身波动就比较大,通过低频采样的数据只能按照低频进行预测,如果在一周中期货价格发生了变化,也无法根据量化模型做出合理的应对,另外影响期货价格的数据也并非在周末统一更新,例如周频发布的螺纹钢库存通常在周四更新而同是周频发布的线螺采购量则可能是周五更新,如果模型统一为周频则有可能错过了最佳的投资入场点。
基于此问题,此篇论文介绍了一种可以处理混频时间序列的神经网络架构,显著-偏置卷积神经网络,并成功用到多个混频金融数据集中,他们发现使用这种网络架构处理混频数据比经典的向量自回归、卷积神经网络和长短期记忆神经网络的效果要好,虽然次中方法还尚在研究阶段,但是由于其新颖的网络构造方法和应用前景而值得了解。
论文介绍:
本篇paper首先介绍了显著-偏执卷积神经网络架构,然后尝试利用周频的螺纹钢库存数据和日频的螺纹钢期货主力数据进行预测,发现这种网络架构在处理混频数据上具有一定的潜力。
在同频率时间序列的处理上,宏观经济或者计量用的较多的是自回归或者是向量回归和向量自回归移动平均等线性模型,这类模型的优势是模型的参数是可观测因子的系数,通过检测因子的统计显著性可以分析出因子对待预测变量的影响,因而能够显著研究人员与经济变量直接的因果关系。在混频时间序列的处理上,则通常会使用状态空间模型,即假设存在一系列不可观测的状态,这些不可观测状态往往代表的是低频因子,再通过可观测的高频数据对不可观测的状态进行推断,最后根据这些状态进行预测。虽然这些传统的经济学模型具有良好的可解释性,但是其简单的线性关系在预测的准确度上往往有一定的欠缺。
当前在预测方面的研究热点是深度神经网络模型,这类模型在nlp和cv等领域都取得了较好的预测效果,但是这类模型的一个缺点是模型不具备可解释性,将它直接应用到期货市场上有一定的风险,因为在经济学中强调的是变量之间的因果关系,但是期货市场更加强调的是预测的准确性。如果在预测的时候模型能够具备可解释性和准确性这两个方面,那么对于金融数据的预测将是一个突破性的发展,同时金融时间序列的预测与语言序列的特征并非完全一致,这意味着直接把经典的深度学习模型应用在金融序列上仍需要进行改进。
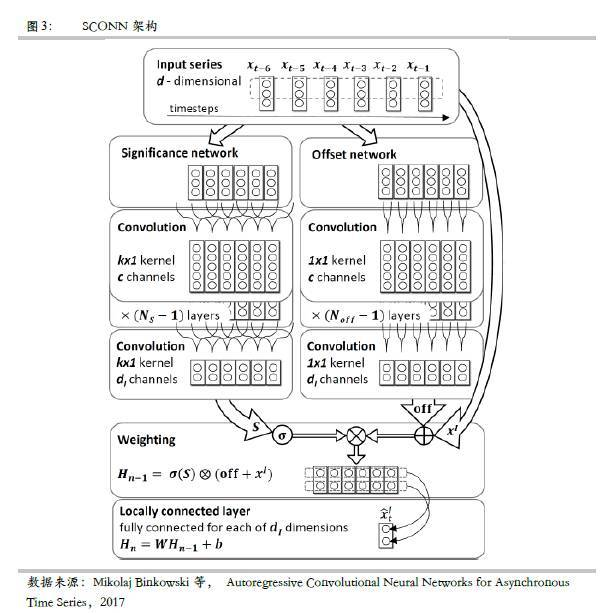
在这种背景下,作者提出了显著-偏置卷积神经网络,这种网络架构把传统的经济学自回归模型与深度学习相结合用于处理混频时间序列的预测。这种模型的原理是仿照自回归模型保留预测变量的时间序列特征,而该时间序列的权重不再是简单的固定系数,而是一个卷积神经网络,同时此网络也具有神经网络的选通机制。

模型原理:
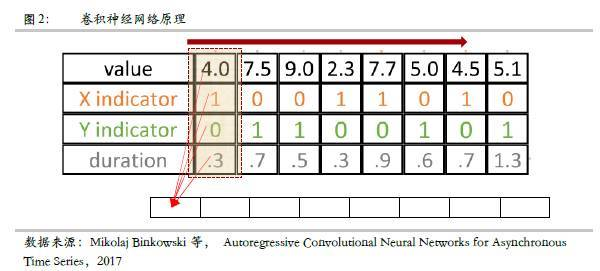
在期货预测中使用到的变量因子通常都是在不同时间点观测得到的,例如螺纹钢期货的收盘价在每天收盘后获得,而螺纹钢库存则通常在周四下午公布,如果周四是非交易日,则没有螺纹钢期货的收盘价,而库存的发布由于节假日等的原因有可能延迟发布。这些不同频率的时间序列很难利用传统的同频率模型进行处理。所以作者在处理这个问题时,他们首先把多维混频的时间序列使用一种新的方法表示,如下图所示,图中包含了X和Y两个不同频率采样的时间序列。由于采样时间完全不一样,这两个时间序列的值可以合并到一个维度,然后再分别使用X和Y两个指标来表示当前列的意义,还有一个维度就是用来表示该值持续的时间间隔。例如第一列中X指示的值为1,Y指示的值为0表明的是当前时间序列上的值为X= 4.0,持续时间间隔为0.3,第二列X指示的值为0,Y指示的值为1,表明当前时间序列上的值为Y=7.5,持续时间为0.7,(这里的持续时间表明的是一个因子的观测时间可能是不同的,那么就会产生时间差,在计算这样的的时间差的时候,比如一个因子的值发布在周三,另外一个因子的值发布在周四,那个可以看成这里的时间差为1个单位)

采用这种混频数据格式的一个好处就是混频数据的表示更加紧凑,每个数据维度不需要单独的时间表示,取而代之的是用0和1标记数据的维度,即使不同维度的数据长度可能不同,这种数据仍然可以紧凑的用矩阵表示。
卷积神经网络的基本原理:
显著-偏置神经网络由卷积网络堆积而成,上面标识的这种网络可以直接作为输入读入,在这里使用的是一维的卷积核,长度为4,该卷积核相当于一个4维的向量,然后点乘下表中,每一列的值,由左往右进行,如果输入的时间序列有8列则经过这一层卷积后序列本来有32个数据,经过一个filter之后,序列的数据变成了8个,如果同时有两个filter,则序列的数据变成了16,然后再经过一层激活函数激活,则构成了深度神经网络。

SOCNN应用实例
与经典的卷积神经网络相比,SOCNN没有使用pooling layer,所以输入的 时间序列的长度能够一直保持到最后的全连接层。正是这种做法才部分保留了神经网络最终输出的可解释性,即可以使用显著网络的权重对某个时间点上变量的显著性做出分析。但另一个方面如果选取的时间序列的长度过长的话,则包含的数据实际的维度再每个样本中可能不一致。
本文主要使用的是SOCNN预测螺纹钢期货主力合约的收益率,预测是基于每周发布的螺纹钢库存以及主力期货合约的日度收盘价这两个因子,训练样本的长度维10个交易日,通常包含一到两个周频数据,数据的格式已经在图一中展示,用于预测下个交易日期货的收益率,使用的数据维螺纹钢主力期货的日收益率和库存的周度变化率,使用的数据是螺纹钢主力期货的日收益率和库存的周度变化率,数据日期从3009年3月至2017年11月,约2500个交易日。SOCNN的训练使用简单的交叉验证法,约70%的样本用于训练,10%的样本用于验证集,20%的样本用作测试集。神经网络训练时使用提早停止的方法,即验证集误差开始增大时停止,神经网络的超参数包括隐藏层神经元数量,学习速度和主成分个数。
结果讨论:
本报告首先对作者提出的SOCNN瓦盖罗解释了原理、框架和数据组织方法。这种网络架构主要是为了适应混频的金融时间序列,其主要原理是使用了多重卷积网络对混频时间序列进行提取,然后计算时间序列上各个节点的权重,所以构造出的神经网络作者认为是部分可解释的。