scikit-learning教程（二）统计学习科学数据处理的教程

统计学习：scikit学习中的设置和估计对象

数据集

Scikit学习处理来自以2D数组表示的一个或多个数据集的学习信息。它们可以被理解为多维观察的列表。我们说这些阵列的第一个轴是样本轴，而第二个轴是特征轴。

scikit：iris数据集附带的一个简单示例

>>>
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> data = iris.data
>>> data.shape
(150, 4)

它由150个鸢尾观察组成，每个由4个特征描述：它们的萼片和花瓣的长度和宽度，详见 iris.DESCR。

当数据最初不是形状时，需要进行预处理才能被scikit学习使用。(n_samples, n_features)

重新组合数据的示例将是数字数据集

../../_images/sphx_glr_plot_digits_last_image_001.png

数字数据集由手写数字的1797 8×8图像组成

>>>
>>> digits = datasets.load_digits()
>>> digits.images.shape
(1797, 8, 8)
>>> import matplotlib.pyplot as plt 
>>> plt.imshow(digits.images[-1], cmap=plt.cm.gray_r) 
<matplotlib.image.AxesImage object at ...>

要将此数据集与scikit一起使用，我们将每个8x8图像转换为长度为64的特征向量

>>>
>>> data = digits.images.reshape((digits.images.shape[0], -1))

估计对象¶

拟合数据：由scikit学习实现的主要API是估计量。估计是从数据中学到的任何对象; 它可以是从原始数据中提取/过滤有用特征的分类，回归或聚类算法或变换器。

所有估计器对象都会公开一个fit采用数据集（通常为2-d数组）的方法：

>>>
>>> estimator.fit(data)

估计器参数：估计器的所有参数可以在实例化时设置，或通过修改相应的属性：

>>>
>>> estimator = Estimator(param1=1, param2=2)
>>> estimator.param1
1

估计参数：当数据与估计器配合时，根据手头的数据估算参数。所有估计的参数是以下划线结尾的估计对象的属性：

>>>
>>> estimator.estimated_param_ 

监督学习：从高维观察中预测输出变量

在监督学习中解决了这个问题

受监督的学习包括学习两个数据集之间的联系：观察数据X和y我们试图预测的外部变量，通常称为“目标”或“标签”。最常见的 y是长度为1D的1D阵列n_samples。

scikit-learn中的所有监督估计都实施了一种适合模型的方法，并且给出了未标记观察值返回预测标签的方法。fit(X, y)predict(X)Xy

词汇：分类和回归

如果预测任务是将一组有限标签中的观测值进行分类，换句话说，将“观察到”对象命名为该任务，则该任务被称为分类任务。另一方面，如果目标是预测连续的目标变量，那么这被称为回归任务。

在scikit学习中进行分类时，y是整数或字符串的向量。

注意：有关scikit学习中使用的基本机器学习词汇的快速浏览，请参阅使用scikit-learning教程的机器学习简介。

最近的邻居和维度的诅咒

虹膜分类：

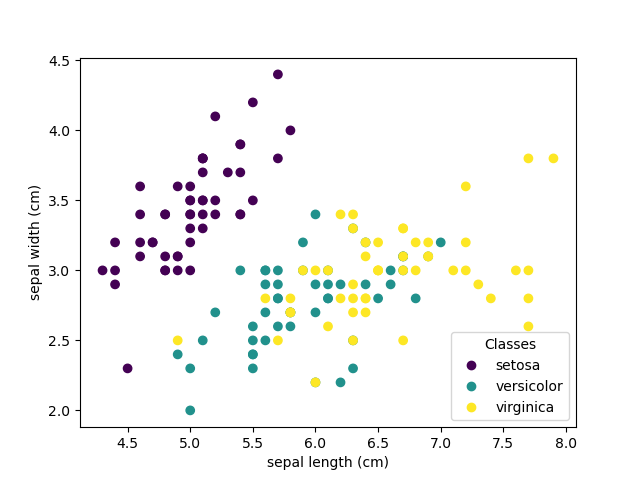
../../_images/sphx_glr_plot_iris_dataset_001.png

虹膜数据集是一个分类任务，包括从花瓣和萼片长度和宽度确定3种不同类型的虹膜（Setosa，Versichelour和Virginica）：

>>>
>>> import numpy as np
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris_X = iris.data
>>> iris_y = iris.target
>>> np.unique(iris_y)
array([0, 1, 2])

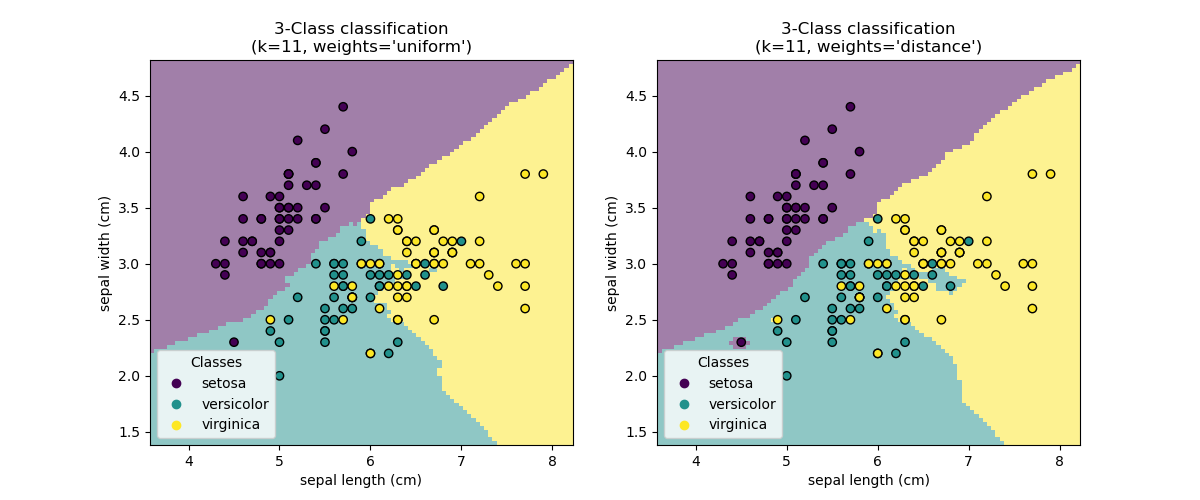
k最近邻居分类器

最简单的分类器是最近的邻居：给出一个新的观察X_test结果，在最近的特征向量的训练集（即用于训练估计的数据）中找到观察值。（有关此类型的分类器的更多信息，请参阅在线Scikit学习文档的最近邻居部分。）

培训集和测试集

在对任何学习算法进行实验的同时，重要的是不要测试估计器对用于拟合估计器的数据的预测，因为这不会评估估计器对新数据的性能。这就是为什么数据集通常被分为列车和测试数据。

KNN（k最近邻）分类示例：

../../_images/sphx_glr_plot_classification_001.png

>>>
>>> # Split iris data in train and test data
>>> # A random permutation, to split the data randomly
>>> np.random.seed(0)
>>> indices = np.random.permutation(len(iris_X))
>>> iris_X_train = iris_X[indices[:-10]]
>>> iris_y_train = iris_y[indices[:-10]]
>>> iris_X_test  = iris_X[indices[-10:]]
>>> iris_y_test  = iris_y[indices[-10:]]
>>> # Create and fit a nearest-neighbor classifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier()
>>> knn.fit(iris_X_train, iris_y_train) 
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
           weights='uniform')
>>> knn.predict(iris_X_test)
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
>>> iris_y_test
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])

维度的诅咒

要使估计器有效，您需要相邻点之间的距离小于某个值 $ð$ ，这取决于问题。在一个维度上，这需要平均 $n〜1 / d$ 分。在上述 $ķ$ -NN示例的上下文中，如果仅通过一个值从0到1和 $ñ$ 训练观察值来描述数据，则新数据将不再远离 $1 / n的$ 。因此，与 $1 / n的$ 类之间特征变化的规模相比，最近的邻居决策规则将很小。

如果功能的数量是 $p$ ，您现在需要 $n〜1 / d ^ p$ 积分。假设我们在一个维度上需要10点：现在 $10 ^ P$ 需要 $p$ 维度的点来铺平 $[0，1]$ 空间。随着 $p$ 数量的增加，良好的估计量所需的培训点数量呈指数增长。

例如，如果每个点只是一个单个数字（8个字节），那么在 $ķ$ 微小 $P〜20$ 维度上的有效-NN估计器将需要比当前估计的整个互联网大小（±1000 埃字节数）更多的训练数据。

这被称为维度的诅咒，是机器学习地址的核心问题。

线性模型：从回归到稀疏

糖尿病数据集

糖尿病数据组包括442例患者的10个生理变量（年龄，性别，体重，血压），以及一年后疾病进展的指标：

>>>
>>> diabetes = datasets.load_diabetes()
>>> diabetes_X_train = diabetes.data[:-20]
>>> diabetes_X_test  = diabetes.data[-20:]
>>> diabetes_y_train = diabetes.target[:-20]
>>> diabetes_y_test  = diabetes.target[-20:]

手头的任务是预测生理变量的疾病进展。

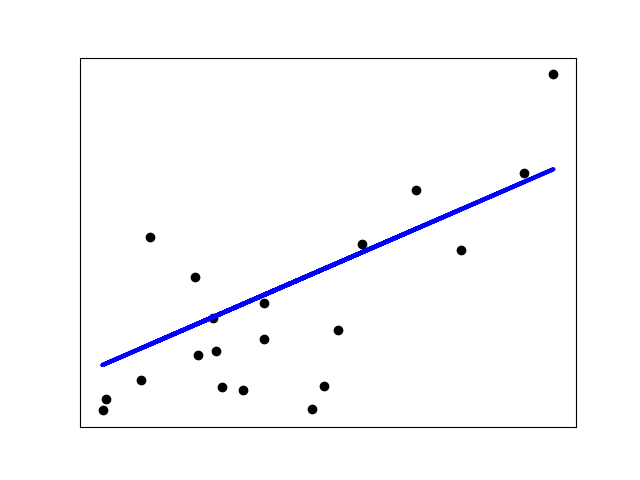
线性回归

LinearRegression在其最简单的形式中，通过调整一组参数将线性模型适用于数据集，以使模型的平方残差之和尽可能小。

线性模型： $y = X beta + epsilon$

$X$ ：数据

$ÿ$ ：目标变量

$公测$ ：系数

$小量$ ：观察噪音

>>>
>>> from sklearn import linear_model
>>> regr = linear_model.LinearRegression()
>>> regr.fit(diabetes_X_train, diabetes_y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> print(regr.coef_)
[   0.30349955 -237.63931533  510.53060544  327.73698041 -814.13170937
  492.81458798  102.84845219  184.60648906  743.51961675   76.09517222]

>>> # The mean square error
>>> np.mean((regr.predict(diabetes_X_test)-diabetes_y_test)**2)
2004.56760268...

>>> # Explained variance score: 1 is perfect prediction
>>> # and 0 means that there is no linear relationship
>>> # between X and y.
>>> regr.score(diabetes_X_test, diabetes_y_test) 
0.5850753022690...

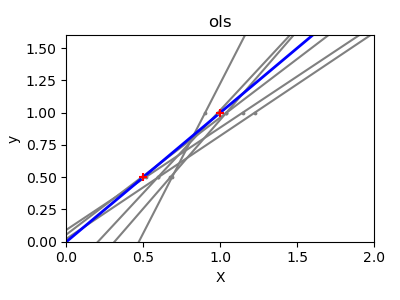
收缩

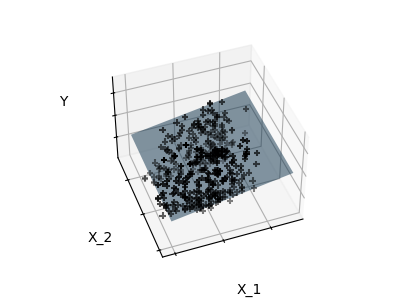
如果每个维度上的数据点很少，则观测值中的噪声会导致高方差：

../../_images/sphx_glr_plot_ols_ridge_variance_001.png

>>>
>>> X = np.c_[ .5, 1].T
>>> y = [.5, 1]
>>> test = np.c_[ 0, 2].T
>>> regr = linear_model.LinearRegression()

>>> import matplotlib.pyplot as plt 
>>> plt.figure() 

>>> np.random.seed(0)
>>> for _ in range(6): 
...    this_X = .1*np.random.normal(size=(2, 1)) + X
...    regr.fit(this_X, y)
...    plt.plot(test, regr.predict(test)) 
...    plt.scatter(this_X, y, s=3)  

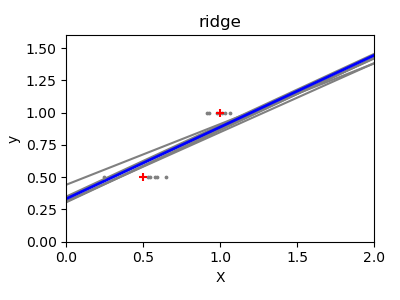
高维统计学习的一个解决方案是将回归系数缩小到零：任意两个随机选择的一组观察值可能是不相关的。这被称为Ridge 回归：

../../_images/sphx_glr_plot_ols_ridge_variance_002.png

>>>
>>> regr = linear_model.Ridge(alpha=.1)

>>> plt.figure() 

>>> np.random.seed(0)
>>> for _ in range(6): 
...    this_X = .1*np.random.normal(size=(2, 1)) + X
...    regr.fit(this_X, y)
...    plt.plot(test, regr.predict(test)) 
...    plt.scatter(this_X, y, s=3) 

这是偏差/方差折衷的一个例子：脊 alpha参数越大，偏差越高，方差越小。

我们可以选择alpha最小化遗漏错误，这次使用糖尿病数据集而不是我们的合成数据：

>>>
>>> alphas = np.logspace(-4, -1, 6)
>>> from __future__ import print_function
>>> print([regr.set_params(alpha=alpha
...             ).fit(diabetes_X_train, diabetes_y_train,
...             ).score(diabetes_X_test, diabetes_y_test) for alpha in alphas]) 
[0.5851110683883..., 0.5852073015444..., 0.5854677540698..., 0.5855512036503..., 0.5830717085554..., 0.57058999437...]

注意

捕获适合的参数噪声阻止模型推广到新数据称为过拟合。由山脊回归引入的偏差称为正则化。

稀疏

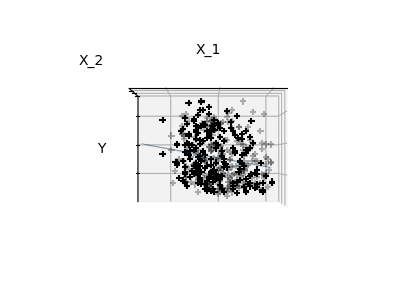
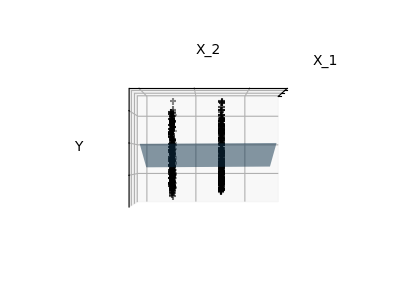
配件只有功能1和2

注意

完整的糖尿病数据集的表示将涉及11个维度（10个特征维度和目标变量之一）。很难在这种表现上形成一种直觉，但是请记住，这将是一个相当空白的空间，这可能是有用的。

我们可以看到，虽然功能2在整个模型上具有很强的系数，但它在y功能1考虑的时候传达了很少的信息。

为了改善问题的调节（即减轻维度的诅咒），只需选择信息特征并设置非信息特征（如特征2至0）将是有趣的。脊回归将减少其贡献，但不设置他们为零。另一种惩罚方法叫做Lasso（最小绝对收缩和选择算子）可以将一些系数设置为零。这种方法被称为稀疏方法，稀疏性可以看作是奥卡姆剃须刀的一个应用：更喜欢更简单的模型。

>>>
>>> regr = linear_model.Lasso()
>>> scores = [regr.set_params(alpha=alpha
...             ).fit(diabetes_X_train, diabetes_y_train
...             ).score(diabetes_X_test, diabetes_y_test)
...        for alpha in alphas]
>>> best_alpha = alphas[scores.index(max(scores))]
>>> regr.alpha = best_alpha
>>> regr.fit(diabetes_X_train, diabetes_y_train)
Lasso(alpha=0.025118864315095794, copy_X=True, fit_intercept=True,
   max_iter=1000, normalize=False, positive=False, precompute=False,
   random_state=None, selection='cyclic', tol=0.0001, warm_start=False)
>>> print(regr.coef_)
[   0.         -212.43764548  517.19478111  313.77959962 -160.8303982    -0.
 -187.19554705   69.38229038  508.66011217   71.84239008]

不同的算法相同的问题

可以使用不同的算法来解决相同的数学问题。例如Lasso，scikit-learn中的对象使用坐标方法解决了套索回归问题，这对大型数据集是有效的。然而，scikit学习还LassoLars使用LARS algorthm 来提供对象，这对于估计的权重向量非常稀疏的问题（即，很少观察的问题）是非常有效的。

分类

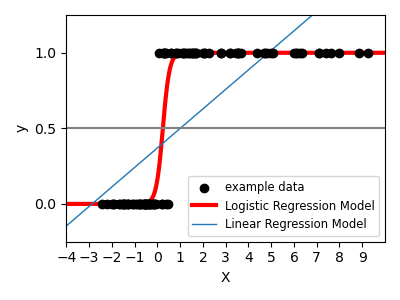
../../_images/sphx_glr_plot_logistic_001.png

对于分类，如在标签虹膜任务中，线性回归不是正确的方法，因为它将对决策前沿的数据给予太多的重视。线性方法是拟合S形函数或逻辑函数：

$y = textrm {sigmoid}（X beta - textrm {offset}）+ epsilon = frac {1} {1 + textrm {exp}（ - X beta + textrm {offset}）} + 小量$

>>>
>>> logistic = linear_model.LogisticRegression(C=1e5)
>>> logistic.fit(iris_X_train, iris_y_train)
LogisticRegression(C=100000.0, class_weight=None, dual=False,
          fit_intercept=True, intercept_scaling=1, max_iter=100,
          multi_class='ovr', n_jobs=1, penalty='l2', random_state=None,
          solver='liblinear', tol=0.0001, verbose=0, warm_start=False)

这被称为LogisticRegression。

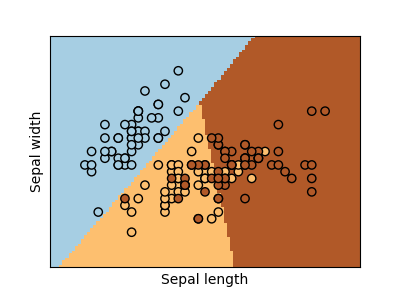
../../_images/sphx_glr_plot_iris_logistic_001.png

多类分类

如果您有几个类来预测，通常使用的选项是适合一对所有分类器，然后使用投票启发式进行最终决策。

收缩和稀疏与逻辑回归

该C参数控制LogisticRegression对象中的正则化量：一个较大的值，C导致较少的正则化。 penalty="l2"给出收缩（即非稀疏系数），同时 penalty="l1"给出稀疏性。

行使

尝试用最近的邻居和线性模型对数字数据集进行分类。留下最后10％，并对这些观察结果进行测试。

from sklearn import datasets, neighbors, linear_model

digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target

解： ../../auto_examples/exercises/digits_classification_exercise.py

支持向量机（SVM）

线性支持向量机

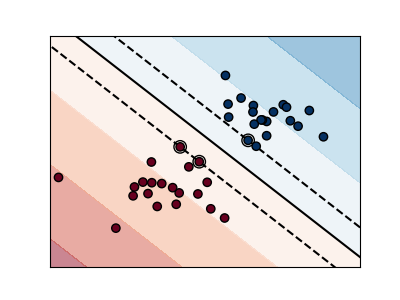
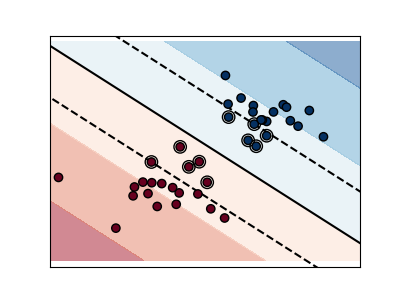
支持向量机属于判别模型族：他们试图找到样本的组合，以构建最大化两个类之间的边界的平面。正则化由C参数设置：一个小值C表示使用分隔线周围的许多或全部观测值计算边际（更正则化）; C意味着利用靠近分离线的观测值计算边际值（较小的正则化）。

非规则SVM	正则SVM（默认）

例：

在虹膜数据集中绘制不同的SVM分类器

SVM可用于回归 - SVR（支持向量回归） - 或分类 - SVC（支持向量分类）。

>>>
>>> from sklearn import svm
>>> svc = svm.SVC(kernel='linear')
>>> svc.fit(iris_X_train, iris_y_train)    
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)

警告

归一化数据

对于包含SVM的许多估计器，具有每个特征的单位标准偏差的数据集对于获得良好的预测是重要的。

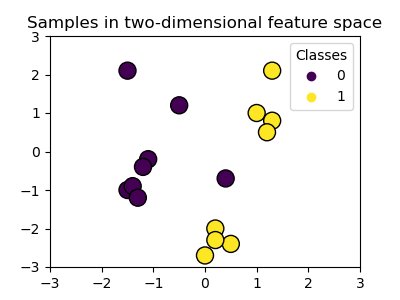
使用内核

在特征空间中，类并不总是线性分离。解决方案是构建不是线性的但可以是多项式的决策函数。这是通过使用内核技巧来完成的，可以通过将内核定位在观察结果上来创建决策能量：

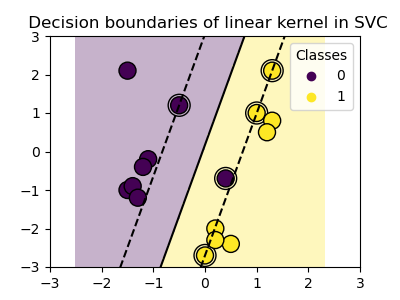
线性内核	多项式内核

>>> >>> svc = svm 。SVC （kernel = 'linear' ）	>>> >>> svc = svm 。SVC （kernel = 'poly' ， ... degree = 3 ） >>> ＃度：多项式度

RBF核（径向基函数）

>>>
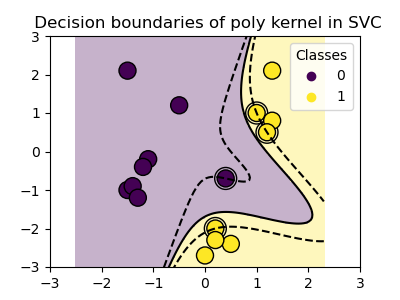>>> svc  =  svm 。SVC （kernel = 'rbf' ）
>>> ＃gamma：
>>> ＃径向内核的大小的倒数

互动的例子

请参阅SVM GUI下载 svm_gui.py; 使用右键和左键添加两个类的数据点，适合模型并更改参数和数据。

行使

尝试从具有SVM的虹膜数据集中分类1和2类，具有2个第一个特征。排除每个类别的10％，并对这些观察结果进行测试预测。

警告：课程是有序的，不要遗漏最后的10％，你只能在一个班上进行测试。

提示：您可以使用decision_function网格上的方法来获得直觉。

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y != 0, :2]
y = y[y != 0]

解： ../../auto_examples/exercises/plot_iris_exercise.py

相关阅读:
排球教练积分程序
 排球积分程序
 排球积分程序
 14周总结
 本周总结
 排球计分规则
 我与计算机
 排球计分程序
 《如何成为一个高手》观后感
 十八周总结
原文地址：https://www.cnblogs.com/wanglei0103/p/7240170.html