1. 前言
集合是由一组无序且唯一(即不能重复)的项组成的。你可以把集合想象成一个既没有重复元素,也没有顺序概念的数组。在ES6中已经内置了集合这一数据结构——Set。接下来,我们就用原生JS来实现这一数据结构。
2. 创建集合类
首先,我们先创建一个集合类,并且为其声明一些实例方法,如下:
class Set {
constructor() {
this.items = {}
}
has(value) {}
add(value) {}
remove(value) {}
clear() {}
size() {}
values() {}
union(otherSet) {}
intersection(otherSet) {}
difference(otherSet){}
isSubset(otherSet){}
}
在上述代码中,我们使用对象而不是数组来表示集合(items),这是因为集合中的元素都是唯一的,而JavaScript的对象不允许一个键指向两个不同的属性,刚好满足集合这一性质。在创建好Set类后,我们还为其声明了一些方法:
- add(value):向集合添加一个新的项。
- remove(value):从集合删除一个值。
- has(value):判断一个值是否存在于集合中,返回
true,否则返回false。 - clear():清空集合。
- size():返回集合所包含元素的数量。
- values():返回一个包含集合中所有值的数组。
- union(otherSet) :求当前集合与给定集合
otherSet的并集。 - intersection(otherSet):求当前集合与给定集合
otherSet的交集。 - difference(otherSet):求当前集合与给定集合
otherSet的差集。 - isSubset(otherSet):判断当前集合是否为给定集合
otherSet的子集。
3. 方法实现
3.1 has(value)
首先要实现的是has(value)方法。这是因为它会被其他方法调用。该方法用来判断一个值是否存在于集合中,返回true,否则返回false。如下:
// 判断value是否存在于集合内,返回true或false
has(value) {
return this.items.hasOwnProperty(value)
}
我们将集合内所有元素在items中都以如下方式存储:
this.items = {
'元素1':'元素1',
'元素2':'元素3',
'元素3':'元素3',
//...
}
我们对象内的让每一对key和value都相等,表示一个元素。当我们需要判断一个值是否存在于集合中,我们只需判断该值是否为对象的属性即可,所以我们可以直接调用hasOwnProperty方法。
3.2 add(value)
该方法用来向集合内添加一个新的项,实现如下:
// 向集合内添加一个数据,成功返回true,失败返回false
add(value) {
if (this.has(value)) {
return false
}
this.items[value] = value
return true
}
由于集合内不允许有重复元素,所以在添加之前先判断要添加的元素是否已经存在于集合内,如果已存在,则返回false,不让添加。否则,将新元素通过对象赋值的方式加入集合内。
3.3 remove(value)
该方法用来从集合删除一个值。实现如下:
// 从集合内删除一个数据
remove(value) {
if (this.has(value)) {
delete this.items[value]
return true;
}
return false;
}
删除之前先判断要删除的元素是否存在于集合内,如果存在,就采用对象删除自身属性的方式将该元素从集合内删除,最后返回true。如果不存在,则返回false。
3.4 size()
该方法用来获取集合中元素的数量。实现如下:
size() {
return Object.keys(this.items).length
}
Object类有一个keys方法,它返回一个包含给定对象所有属性的数组。我们可以通过这个数组的length属性来获取到items对象的属性个数。
3.5 values()
该方法用于获取一个包含集合中所有值的数组。实现如下:
// 以数组形式返回集合内的所有元素
values() {
return Object.keys(this.items)
}
同size()方法实现一样,Object.keys方法返回一个包含给定对象所有属性的数组。
3.6 clear()
该方法用于将集合清空,即删除集合内的所有元素。实现如下:
// 清空集合
clear() {
this.items = {}
}
清空集合,即就是把this.itmes变成空对象,那我们直接将空对象{}赋值给this.items即可。
3.7 union(otherSet)
该方法用于求当前集合与给定集合otherSet的并集。
并集的数学概念是集合A和集合B的并集,表示为:
该集合定义如下:
意思是x(元素)存在于A中,或x存在于B中。下图展示了并集操作:
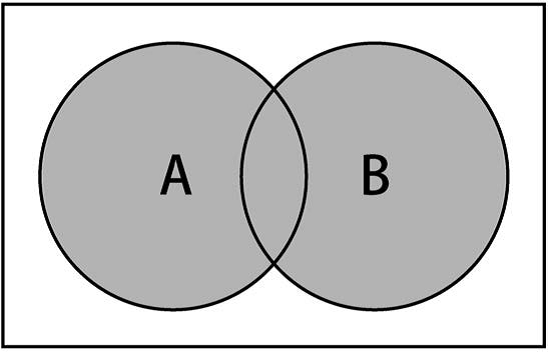
实现如下:
// 求并集
union(otherSet) {
let unionSet = new Set() // 创建一个新的集合,用于存储两个集合的并集
let values = this.values(); //获取第一个集合(当前的Set类实例)所有的值
for (let i = 0; i < values.length; i++) { // 遍历并全部添加到代表并集的集合中
unionSet.add(values[i]);
}
values = otherSet.values(); // 第二个集合同理
for (let i = 0; i < values.length; i++) {
unionSet.add(values[i]);
}
return unionSet;
}
首先需要创建一个新的集合,代表两个集合的并集。接下来,获取第一个集合(当前的Set类实例)所有的值,遍历并全部添加到代表并集的集合中。然后对第二个集合做同样的事。最后返回结果。
3.8 intersection(otherSet)
该方法用于求当前集合与给定集合otherSet的交集。
交集的数学概念是集合A和集合B的交集,表示为:
该集合定义如下:
意思是x(元素)存在于A中,且x存在于B中。下图展示了交集操作:
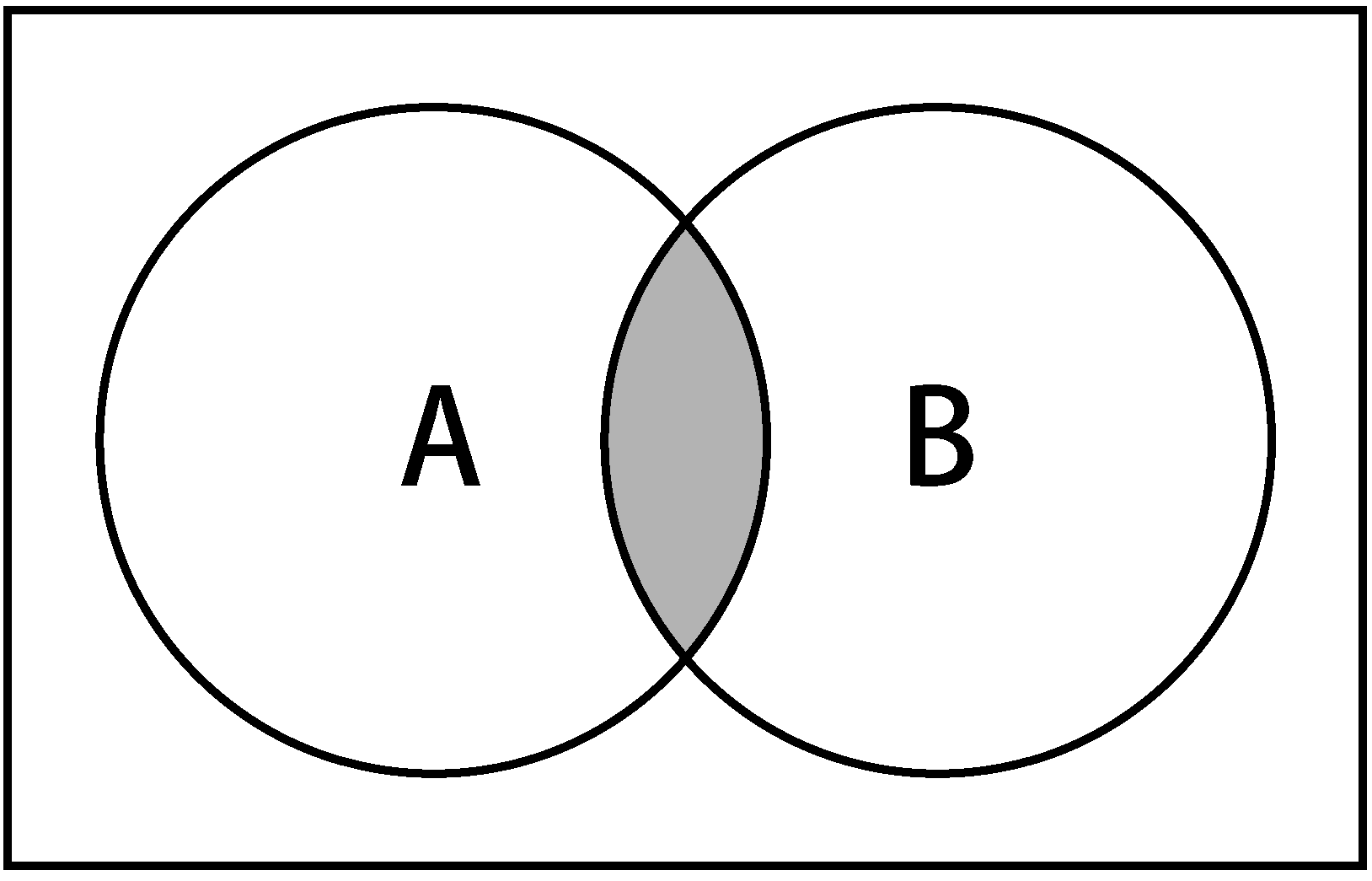
实现如下:
// 求交集
intersection(otherSet) {
let intersectionSet = new Set() // 创建一个新的集合,用于存储两个集合的交集结果
let values = this.values();
for (let i = 0; i < values.length; i++) { // 遍历当前的集合中的元素,如果这个元素也存在与otherSet,则将该元素存入intersectionSet
if (otherSet.has(values[i])) {
intersectionSet.add(values[i])
}
}
return intersectionSet
}
首先需要创建一个新的集合intersectionSet,代表两个集合的交集。接下来,获取第一个集合(当前的Set类实例)所有的值,遍历并判断每个元素是否存在于集合otherSet中,如果存在,则表示该元素既存在于第一个集合,又存在于第二个集合otherSet中,将其添加到代表交集的集合intersectionSet中。最后返回结果。
3.9 difference(otherSet)
该方法用于求当前集合与给定集合otherSet的差集。
差集的数学概念是集合A和集合B的差集,表示为:
定义如下:
意思是x(元素)存在于A中,且x不存在于B中。下图展示了集合A和B的差集操作:
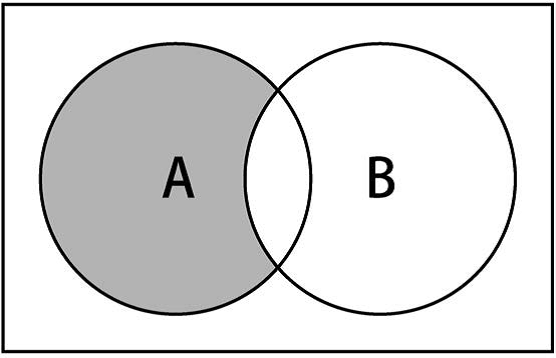
实现如下:
// 求差集
difference(otherSet){
let differenceSet = new Set() // 创建一个新的集合,用于存储两个集合的交集结果
let values = this.values();
for (let i = 0; i < values.length; i++) { // 遍历当前的集合中的元素,如果这个元素不存在于otherSet中,则将该元素存入differenceSet
if (!otherSet.has(values[i])) {
differenceSet.add(values[i])
}
}
return differenceSet
}
首先需要创建一个新的集合differenceSet,代表两个集合的差集。接下来,获取第一个集合(当前的Set类实例)所有的值,遍历并判断每个元素是否存在于集合otherSet中,如果不存在,则表示该元素只存在于第一个集合中,将其添加到代表交集的集合differenceSet中。最后返回结果。
3.10 isSubset(otherSet)
该方法用于判断当前集合是否为给定集合otherSet的子集。
子集的数学概念是集合A是集合B的子集(或集合B包含了A),表示为:
定义如下:
意思是集合A中的每一个x(元素),也需要存在于B中。下图展示了集合A是集合B的子集:
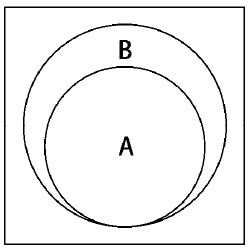
实现如下:
// 判断当前集合是否为otherSet的子集
isSubset(otherSet){
//如果当前实例中的元素比otherSet实例更多,它就不是一个子集。
// 子集的元素个数需要小于或等于要比较的集合。
if (this.size() > otherSet.size()){
return false
}
let values = this.values();
for (let i = 0; i < values.length; i++) { // 遍历当前的集合中的元素,判断这个元素是否存在于otherSet中,
// 如果有一个元素不存在于otherSet中,则表明不是子集
if (!otherSet.has(values[i])) {
return false
}
}
return true
}
首先判断当前集合的长度是否大于给定集合的长度,如果大于,则肯定不是给定集合的子集,因为子集的元素个数必须小于或等于要比较的集合。接下来要遍历集合中的所有元素,验证这些元素也存在于otherSet中。如果有任何元素不存在于otherSet中,就意味着它不是一个子集,返回false。如果所有元素都存在于otherSet中,则表明当前集合是给定集合的子集,返回true。
4. 总结
以上就是实现了集合这一数据类型,包括其6个实例方法:has(value) 、 add(value) 、 remove(value) 、 clear() 、size() 、values() ;和3个集合操作方法: union(otherSet) 、intersection(otherSet) 、 difference(otherSet) 、isSubset(otherSet) 。完整代码请戳☞☞☞Set
(完)