---------------------------------
大数定律:大量样本数据的均值(样本值之和除以样本个数),近似于随机变量的期望(标准概率*样本次数)。(样本(部分)趋近于总体)
中心极限定理:大量样本数据的均值(或者样本和众数、极差等等,或者任意的非正态的分布都可以)的频率分布,服从正态分布(样本越大,越吻合正态分布)。
大数定律研究的是在什么条件下,这组数据依概率收敛于他们的均值。
中心极限定理研究的是在什么条件下,这些样本依分布收敛于正太分布。
依概率收敛就是强收敛,随机过程中成为强平稳。依分布收敛就是弱收敛,随机过程中成为弱平稳。
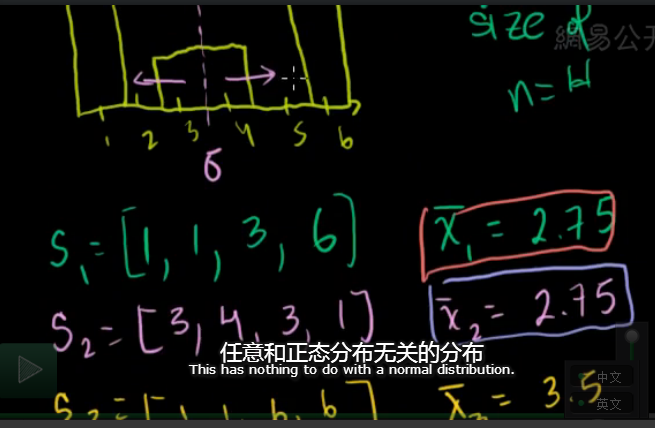

the size of sample is 4,and mean of it is as aboved.
size--> infinit. approach of normal distribution.
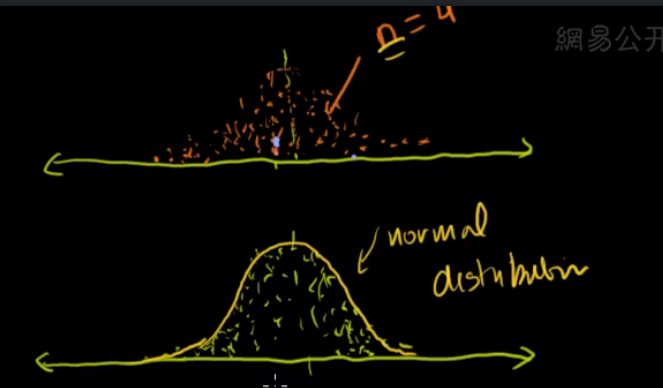
--------------------------------------------------------
如何证明“分布函数右连续”

关于分布函数右连续,不是特别理解,求助_概率论与数理统计吧_百度贴吧
https://tieba.baidu.com/p/4522353705
整理图片

------------------------
我们学过的各种分布的应用有:
0-1分布:抛一次硬币,新生儿的性别登记,产品质量的合格与否,电力消耗是否超负荷;
二项分布:射击击中与否的概率,机器是否发生故障;
泊松分布:主要描述大量重复实验中稀有事件发生的次数,即小概率事件,如一本书一页的印刷的错误数、某地区一天邮递遗失的信件数、某一天医院的急诊病人数、一段时间发生交通事故的概率;
几何分布:为了刷到某一分数而参加考试的次数,刷到理想分数就停止;
均匀分布:人工栽培的有一定的均匀间距的树木,从头到尾的排队的人数等;
指数分布:旅客进入机场的时间间隔、许多电子产品的寿命,但人的寿命不属于指数分布;
正态分布:一个地区的男性成年人的身高、测量某零件长度的误差,海洋波浪的高度、半导体器件中的热噪声电流或电压。
需要补的知识点:
课程中所讲授的这几类分布在生活中都有着广泛的应用,譬如:某国家的人的身高、某个省的各个高程值以及 12 岁学生的数学考试分数,这些都是正态分布的应用样例;如果多次抛掷硬币,则在一连串抛币动作中硬币正面朝上的次数也将接近正态分布。在模拟模型中对气体浓度建模时、对某十字路口发生交通事故的时间间隔建模时,以及使用“创建随机点”工具放置随机点时都可以使用均匀分布。在十字路口接连发生的两次交通事故的时间间隔、夜晚在天空两次看到流星的时间间隔,以及街道上各坑洼处之间的距离,这些都是指数分布的典型例子。泊松分布的应用事件可以是十字路口的事故发生次数、出生缺陷数量或一平方公里内驼鹿的数量;此外,泊松分布可以对小概率事件进行建模。
据我了解,概率统计中使用到的分布还有:
整数分布,这是一种离散形式的均匀分布,是指定区间内所有离散值都具有相同概率的一种概率分布状态。
Gamma分布,这是一种连续型概率分布,用于对多个呈指数分布的独立变量的总和建模,可将它视为是指数分布的特例。
负二项分布,这是一种离散型概率分布。负二项分布是在伯努利试验的基础上得出的。负二项分布可以用来分析要抛掷硬币多少次才能使其连续五次都正面朝上。因此,负二项分布的建模对象是
互为对偶的离散型分布与连续型分布,可以看作是由同一个函数——源函数产生的。源函数的正线性组合、乘积和负导数,仍然是源函数。源函数揭示了互为对偶的分布的分布函数之间的相互关系,并能用来求随机变量的数字特征、特征函数、概率母函数、分布的最大值和参数的极大似然估计.
成功之前的失败次数。
-----------------------
贝叶斯公式针对的是某一个过程中已知结果发生求出事件过程的某个条件成立的概率
全概率公式针对的是某一个过程中已知条件求出最后结果的概率
全概率公式是在分块和总的有条件概率的基础上运作的
条件概率相关联与相互独立的关系
相互独立a虽然发生了但是对b不产生任何影响
相互独立:a事件的发生不影响b事件的发生概率
不相容: a事件发生,b一定不发生
独立:没关系
不相容:有关系,互斥
事件A和B的交集为空,A与B就是互斥事件,也叫互不相容事件.指两事件不可能同时发生.
事件A和B的交集不为空,A与B相容.指两事件可能同时发生.
注 意 : (1 1 ) 独 立 事 件 的 条 件 概 率 与 条 件 无 关 ,
(2 2 ) 独 立 事 件 计 算 概 率 尽 可 能 表 示 为 乘 积 事 件.
F(x) 随机变量的分布函数,定义是一个概率;大于等于0,小于等于1
密度函数仅仅要求大于等于零;负无穷到正无穷的积分等于1就可以了,并不要求函数是小于1的
泊松分布最常见的一个应用就是,它作为了排队论的一个输入。
比如在一段时间t(比如 1 个小时)内来到食堂就餐的学生数量肯定不会是一个常数(比如一直是 200 人),而应该符合某种随机规律:
假如在 1 个小时内来 200 个学生的概率是 10%,来 180 个学生的概率是 20%……一般认为,这种随机规律服从的就是泊松分布。

这个
分布是S.-D.泊松研究二项分布的渐近公式时提出来的。泊松分布P (λ)中只有一个参数λ ,它既是泊松分布的均值,也是泊松分布的方差。生活中,当一个随机事件,例如来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布。

其实泊松分布在日常中还是很好辨别的,因为他有一个累计的过程。曾看到一篇用泊松分布来分析美国治安的例子,引来给大家看看: 美国枪击案假定它们满足"泊松分布"的三个条件:
(1)枪击案是小概率事件。
(2)枪击案是独立的,不会互相影响。
(3)枪击案的发生概率是稳定的。
显然,第三个条件是关键。如果成立,就说明美国的治安没有恶化;如果不成立,就说明枪击案的发生概率不稳定,正在提高,美国治安恶化。根据资料,1982--2012年枪击案的分布情况如下:

计算得到,平均每年发生2起枪击案,所以 λ = 2 。

上图中,
蓝色的条形柱是实际的观察值,
红色的虚线是理论的预期值。
可以看到,
观察值与期望值还是相当接近的。
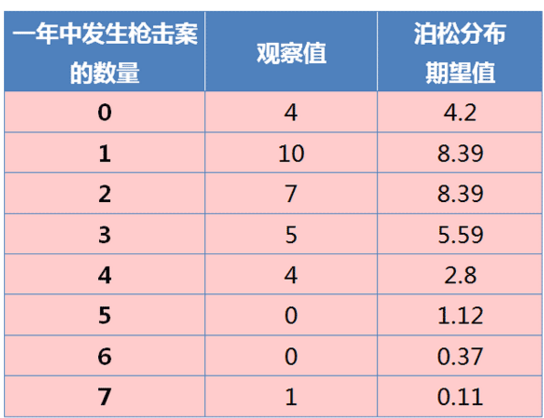
我们用"卡方检验",检验观察值与期望值之间是否存在显著差异。卡方统计量 = Σ[(观察值-期望值)^2/期望值]
计算得到,卡方统计量等于9.82。查表后得到,置信水平0.90、自由度7的卡方分布临界值为12.017。因此,卡方统计量小于临界值,这表明枪击案的观察值与期望值之间没有显著差异。所以,可以接受"发生枪击案的概率是稳定的"假设,也就是说,从统计学上无法得到美国治安正在恶化的结论。
但是,也必须看到,卡方统计量9.82离临界值很接近,p-value只有0.18。也就是说,对于"美国治安没有恶化"的结论,我们只有82%的把握,还有18%的可能是我们错了,美国治安实际上正在恶化。因此,这就需要看今后两年中,是否还有大量枪击案发生。如果确实发生了,泊松分布就不成立了。



PMF( 概率质量函数 ): 是对 离散随机变量 的定义. 是 离散随机变量 在各个特定取值的概率. 该函数通俗来说,就是 对于一个离散型概率事件来说, 使用这个函数来求它的各个成功事件结果的概率.
PDF ( 概率密度函数 ): 是对 连续性随机变量 的定义. 与PMF不同的是 PDF 在特定点上的值并不是该点的概率, 连续随机概率事件只能求一段区域内发生事件的概率, 通过对这段区间进行积分来求. 通俗来说, 使用这个概率密度函数 将 想要求概率的区间的临界点( 最大值和最小值)带入求积分. 就是该区间的概率.
各种分布及应用场合(建模对象)
http://www.360doc.com/content/14/0110/18/15459877_344179498.shtml
在一个时间段内事件平均发生的次数服从泊松分布,这个次数在泊松分布中用lambda表示。这个lambda在指数分布里面的意义基本是一样的,也是在一个时间段内事件平均发生的次数。
泊松分布表示的是事件发生的次数,“次数”这个是离散变量,所以泊松分布是离散随机变量的分布。
指数分布是两件事情发生的平均间隔时间,“时间”是连续变量,所以指数分布是一种连续随机变量的分布。
可以用等公交车作为例子:某个公交站台一个小时内出现了的公交车的数量 就用泊松分布来表示
某个公交站台任意两辆公交车出现的间隔时间 就用指数分布来表示