在机器学习中,有很多的问题并没有解析形式的解,或者有解析形式的解但是计算量很大(譬如,超定问题的最小二乘解),对于此类问题,通常我们会选择采用一种迭代的优化方式进行求解。
这些常用的优化算法包括:梯度下降法(Gradient Descent),共轭梯度法(Conjugate Gradient),Momentum算法及其变体,牛顿法和拟牛顿法(包括L-BFGS),AdaGrad,Adadelta,RMSprop,Adam及其变体,Nadam。
1.梯度下降法(SGD)
梯度下降法的核心思想就是:通过每次在当前梯度方向(最陡的方向)向前前进一步,来逐渐逼近函数的最小值。类似于你站在山峰上,怎样才能最快的下到山脚呢?当然是选择坡度最陡的方向下山最快,这个坡度最陡正是数学上的“导数”概念,但导数没有方向,对此出来了“梯度”z,所以才叫做“梯度下降法”
首先对于机器学习而言,存在模型函数h(θ),以及损失函数J(θ)
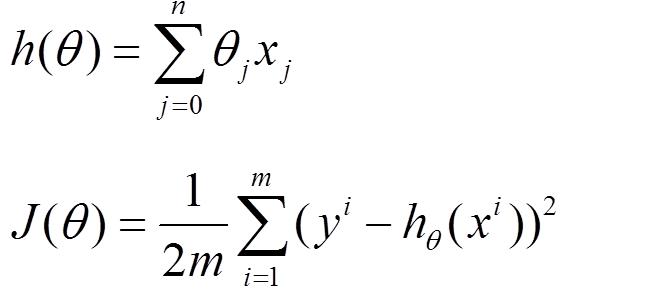
我们将损失函数在θi进行一阶泰勒展开:
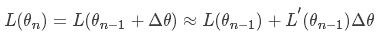
对于大多数博文而言,对应的梯度下降函数会是
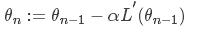
可能大家没有注意到,这里为什么后面变成了负的导数,不应该是正的嘛,这是为什么呢?????其实这里存在的负号很重要
首先,对于损失函数而言,我们的目标是减小损失函数的值,上式中,前面一项不需要解释,后面一项是梯度下降的系数*导数。
损失函数是关于θ的函数,当导数大于0时,损失函数随着θ的减小而减小。对上式而言,此时θ在减小(后面一项小于0),那么相应的损失函数也会相应的减小。
当导数小于0时,损失函数随着θ的增大而减小。对上式而言,此时的θ是在增大的(后面一项大于0),那么相应的损失函数也会相应的减小。
所以这就是为什么这个地方一定是负号,看似简单的数学推到,实则里面蕴藏着数学家很多的心血。
对于梯度下降法,它其实就是在m个样本中,找寻那个使得当前损失函数(不管以后,只看眼睛前)下降最快的方向来进行θ参数的迭代。
但是这种梯度下降法目前使用不多了,因为当数据量非常大时,那么相应的进行一步迭代会非常吃力(需要遍历所有样本,每一次迭代时,每一个样本都要计算,成本太高了)。相应的便产生了随机梯度下降法和批量梯度下降法。引入随机梯度下降法与批量梯度下降法是为了应对大数据量的计算而实现一种快速的求解。
随机梯度下降法:在梯度下降法的基础上,它在每次迭代时,只找一个样本来进行迭代,这样计算量就会减少很多。比如对于一个有几十万的大数据集,使用随机梯度下降法,或许只需要使用几千个数据就可以得到最优的θ,那么此时计算就会快很多,但相应的也存在噪音的干扰,如果出现一些脏数据样本,那么就会对θ的优化产生影响。这种做法相对于梯度下降而言十分极端,因此现在普遍使用批量梯度下降法。
批量梯度下降法:批量梯度下降法中m替换成mini-batch,在此将mini-bach的size远小于m的大小,同时m也是远大于1的。
(1)首先J(θ)对θ求导,得到每个θ对应的梯度:
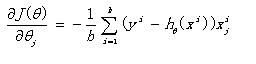
(2)由于最小化损失函数,座椅按照每个参数θ的梯度负方向,来更新θ:
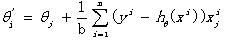
从上面的公式可以看出,每次迭代的时候都是得到局部最优的近似解,然后在进行下一轮的迭代,虽然不是得到全局最优,但是从计算力上却减小了不少的计算量,方便实际操作。(不要太理想化,要投入到实际中去)。
梯度下降(SGD)的评价
优点:操作简单,计算量小,在损失函数是凸函数的情况下能够保证收敛到一个较好的全局最优解。
缺点:1.α是个定值(在最原始的版本),它的选取直接决定了解的好坏,过小会导致收敛太慢,过大会导致震荡而无法收敛到最优解。
2.对于非凸问题,只能收敛到局部最优,并且没有任何摆脱局部最优的能力(一旦梯度为0就不会再有任何变化)。
PS:对于非凸的优化问题,我们可以将其转化为对偶问题,对偶函数一定是凹函数,但是这样求出来的解并不等价于原函数的解,只是原函数的一个确下界
2.Momentum
Momentum的思想就是:模拟物体运动的惯性,比如,当我们跑步要拐弯的时候,我们的拐弯方向是由我们前面跑直线的方向和转弯时的切线方向共同决定,Momentum每次迭代时,会保留上次一部分更新的方向:
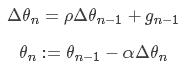
这里ρ值决定了保留多少上次更新方向的信息,值为0~1,初始时可以取0.5,随着迭代逐渐增大;α为学习率,同SGD。
Momentum评价
优点:一定程度上缓解了SGD收敛不稳定的问题,并且有一定的摆脱局部最优的能力(当前梯度为0时,仍可能按照上次迭代的方向冲出局部最优点),直观上理解,它可以让每次迭代的“掉头方向不是那个大“。左图为SGD,右图为Momentum。
缺点:又多了另外一个超参数ρρ需要我们设置,它的选取同样会影响到结果
