Circle Loss: A Unified Perspective of Pair Similarity Optimization
Abstract
本文提出了一种在深度特征学习中使用的成对相似度优化的观点,旨在使类内相似度sp最大化,类间相似度sn最小化。我们发现大多数损失函数,包括triplet损失和softmax交叉熵损失,将sn和sp嵌入到相似对中,并尽力减少(sn−sp)。这种优化方法是不够灵活的,因为每个相似度评分上的惩罚强度都是相等的。我们的直觉是,如果相似度与最佳值相差甚远,就应该予以强调,即惩罚强度应该更大点。为此,我们简单地重新加权每个相似度来突出未优化的相似度分数。由于它的判定边界是圆的,故称Circle loss。对于两种基本深度特征学习范式,即class-level标签学习(即softmax交叉熵损失这种学习方式)和pair-wise标签学习(即triplet损失这种需要构造对的学习方式),Circle loss都有一个统一的公式。通过分析,我们表明,与损失函数优化(sn−sp)相比,Circle loss提供了一种更灵活的优化方法,可以获得更明确的收敛目标。通过实验,我们证明了在各种深度特征学习任务中Circle loss的优越性。在人脸识别、行人再识别以及几个细粒度图像检索数据集上,所取得的性能与目前的技术水平相当。
1. Introduction
本文对两种基本深度特征学习范式——class-level特征学习和pair-wise特征学习——持有同一个相似度优化观点。前者使用分类损失函数(如softmax交叉熵损失[25,16,36])来优化样本与权重向量之间的相似性。后者利用度量损失函数(例如,triplet损失[9,22])来优化样本之间的相似性。在我们的理解中,这两种学习方式并没有本质上的区别。它们都要求类间相似度sn最小,类内相似度sp最大。
从这一观点出发,我们发现许多流行的损失函数(如triplet损失[9,22]、softmax交叉熵损失及其变体[25,16,36,29,32,2])共享类似的优化模式。它们都将sn和sp嵌入到相似对中,并尽力减少(sn−sp)。在(sn−sp)中,增加sp等价于减少sn。我们认为这种对称优化方式容易产生以下两个问题。
- Lack of flexibility for optimization. sn和sp上的惩罚强度是相等的。给定特定的损失函数,sn和sp的梯度具有相同的振幅(详见第2节)。在一些极端情况下,例如,sp很小,sn已经接近0(如图1 (a)中的“A”),它还是继续用较大的梯度来惩罚sn(因为sn已经接近于0了,所以此时的目的应该是增大sp,sn应该梯度较小,sp才应该梯度大)。这是低效和不合理的。

- Ambiguous convergence status. 优化(sn - sp)通常导致决策边界为sp - sn = m (m为边际)。该判定边界允许收敛的模糊(如图1 (a)中的“T”和“ T' ”)。例如,T有{sn, sp} = {0.4, 0.7}, T' 有{s'n, s'p} ={0.2, 0.5}。它们都得到了边际m = 0.3,都被认为是一个好的收敛效果。但是,将它们相互比较,我们发现sn和s'p之间的差距只有0.1。这就导致了A、B、C在收敛时就可以朝着绿色边际线上多个点的方向去收敛,方向不够明确。因此,模糊收敛对特征空间的可分离性进行了妥协。
有了这些见解,我们就有了一种直觉,即不同相似度的分数应有不同的惩罚力度。如果相似度分数与最佳值相差甚远,就应该受到严厉惩罚。否则,如果一个相似度评分已经接近最优,则应该进行温和的优化。为此,我们首先将(sn−sp)推广为(αn sn−αp sp),其中αn和αp是独立加权因子,允许sn和sp以不同的速度学习。然后将αn和αp分别作为sn和sp的线性函数,使学习速度适应优化状态:相似度分数偏离最优值越远(即sp远离1,或sn远离0),权重因子越大。这样的优化导致决策边界αn sn−αp sp = m,在(sn, sp)空间产生一个圆形状,因此我们将所提出的损失函数命名为Circle loss。
简单来说,Circle loss本质上是从以下三个方面重塑了深度特征学习的特征:
First, a unified loss function. 从统一相似对优化的角度出发,我们提出了两种基本学习范式的统一损失函数:class-level标签学习和pair-wise标签学习。
Second, flexible optimization. 在训练过程中,反向传播到sn (sp)的梯度将被αn (αp)放大。那些未优化的相似度分数将有更大的权重因子,从而得到更大的梯度。如图1 (b)所示,A、B、C的优化是不同的。
Third, definite convergence status. 在圆决策边界上,Circle loss支持特定的收敛状态(如图1 (b)中的“T”),见3.3节。相应地设定了明确的优化目标,有利于分离。(即可见图(b)中的T和T'点,T有{sn, sp} = {0.4, 0.7}, T' 有{s'n, s'p} ={0.15, 0.55},与决策边界上的其他点相比,T的sp与sn之间的间隙最小。也就是说,T'在sp和sn之间的间隙更大,本身就更难以维持。因此A、B、C都会朝着T的方向去收敛,十分明确)
本文的主要贡献总结如下:
- 我们提出了Circle loss,一个用于深度特征学习的简单损失函数。通过在监督下对每个相似度分数进行重新加权,Circle loss有利于深度特征学习,优化灵活,收敛目标明确。
- 我们提出了与class-level标签和pair-wise标签兼容的Circle loss。经过轻微的修改,Circle loss可退化为triplet损失或softmax交叉熵损失。
- 我们在各种深度特征学习任务中进行了广泛的实验,如人脸识别、行人再识别、汽车图像检索等。在所有这些任务中,我们展示了Circle loss的优越性,性能与目前的技术水平相当。
2. A Unified Perspective
深度特征学习的目标是最大化类内相似度sp,最小化类间相似度sn。例如,在余弦相似度度量下,我们期望sp→1和sn→0。
为此,使用class-level标签学习和使用pair-wise标签学习是两个基本的范式。它们通常是分开考虑的,从损失函数的角度来看,它们彼此之间有很大的不同。给定class-level标签,首先是学会使用一个分类损失将每个训练样本分类到其目标类别,如L2-Softmax[21]、Large-margin Softmax[15]、Angular Softmax[16]、NormFace[30]、AM-Softmax[29]、CosFace[32]、ArcFace[2]。这些方法也被称为基于代理的学习,因为它们优化了样本和代表每个类的一组代理之间的相似性。相反给定pair-wise标签,直接学习特征空间中的pair-wise相似度(即样本之间的相似性),因此不需要代理,例如,constrastive loss[5,1], triplet loss[9、22], Lifted-Structure loss[19], N-pair loss[24], Histogram loss[27], Angular loss[33], Margin based loss[38], Multi-Similarity loss[34]等等。
本文从统一的角度看待这两种学习方法,既不偏好基于代理的相似度,也不偏好pair-wise相似度。给定特征空间中的单个样本x,假设这里有与x相关的K个类内相似度分数,L个类间相似度分数。我们将该相似度分数分别表示为![]()
![]() 和
和![]()
为了最小化每个![]() 和最大化每个
和最大化每个![]()
![]()
![]() ,我们提出了统一的损失函数:
,我们提出了统一的损失函数:
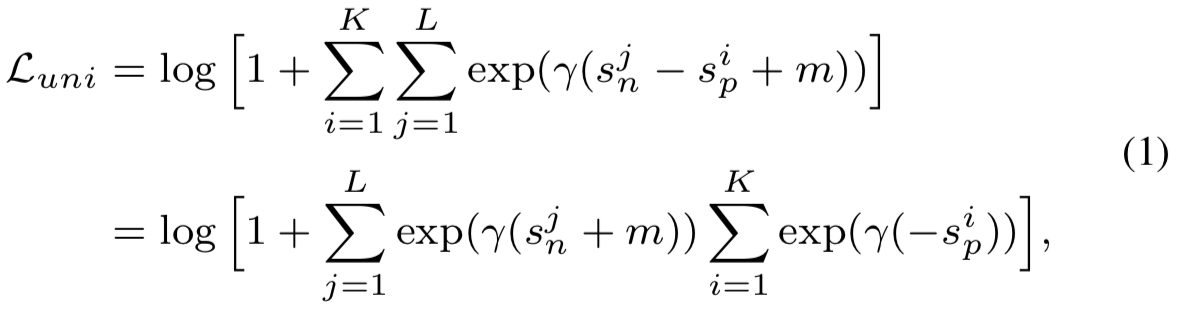
其中![]() 是一个扩展因子,m是用于相似度分离的边际
是一个扩展因子,m是用于相似度分离的边际
等式(1)是直观的。其通过迭代每个相似对去减少(![]() -
- ![]() )。我们注意到,通过简单的调整,可以将其降级为triplet loss或分类损失
)。我们注意到,通过简单的调整,可以将其降级为triplet loss或分类损失
Given class-level labels, 我们计算x和权重向量![]() (N是训练类的数量)的相似度分数。具体说来,我们通过
(N是训练类的数量)的相似度分数。具体说来,我们通过![]()
![]() 得到(N-1)个类间相似度分数。除此之外,我们还使用
得到(N-1)个类间相似度分数。除此之外,我们还使用![]() 得到一个类内相似度分数(省略上标)。有了这些先决条件后,等式(1)降级为了AM-Softmax[29,32],其是Softmax损失(即softmax交叉熵损失)的一个重要变体:
得到一个类内相似度分数(省略上标)。有了这些先决条件后,等式(1)降级为了AM-Softmax[29,32],其是Softmax损失(即softmax交叉熵损失)的一个重要变体:

而且,当m=0时,等式(2)则进一步降级为Normface[30]。通过使用内积和设置![]() =1来替换cosine相似度,其最终将降级为Softmax损失
=1来替换cosine相似度,其最终将降级为Softmax损失
Given pair-wise labels, 我们计算mini-batch中x和其他特征之间的相似度分数。具体来说,就是计算![]()
![]()
![]()
![]() 。相应地,
。相应地,![]() 。等式(1)将降级为使用hard mining[22,8]的triplet损失:
。等式(1)将降级为使用hard mining[22,8]的triplet损失:

(这个式子就是通过求极限,使用洛必达法则上下求导得到最终结果为![]() ,如果是欧式距离,优化方向就是Maximize,如果是余弦相似度,优化方向就是Minimize)
,如果是欧式距离,优化方向就是Maximize,如果是余弦相似度,优化方向就是Minimize)
具体来说,我们注意到在等式(3)中,被Lifted-Structure loss[19], N-pair loss[24], Multi-Similarity loss[34]等实现的![]() 操作实现了样本中的"soft"hard mining。逐渐增大
操作实现了样本中的"soft"hard mining。逐渐增大![]() 会加大mining的强度,当
会加大mining的强度,当![]() 时,则实现的是[22,8]中标准的hard mining。
时,则实现的是[22,8]中标准的hard mining。
Gradient analysis. 等式(2)和等式(3)说明了triplet损失,Softmax损失及其几种变体可以解释为等式(1)的具体情况。换句话说,它们都优化(sn−sp)。在只有单一sp和sn的toy场景下,我们将图2 (a)和(b)中的triplet loss和AM-Softmax loss的梯度可视化,从中我们得到以下观察结果:
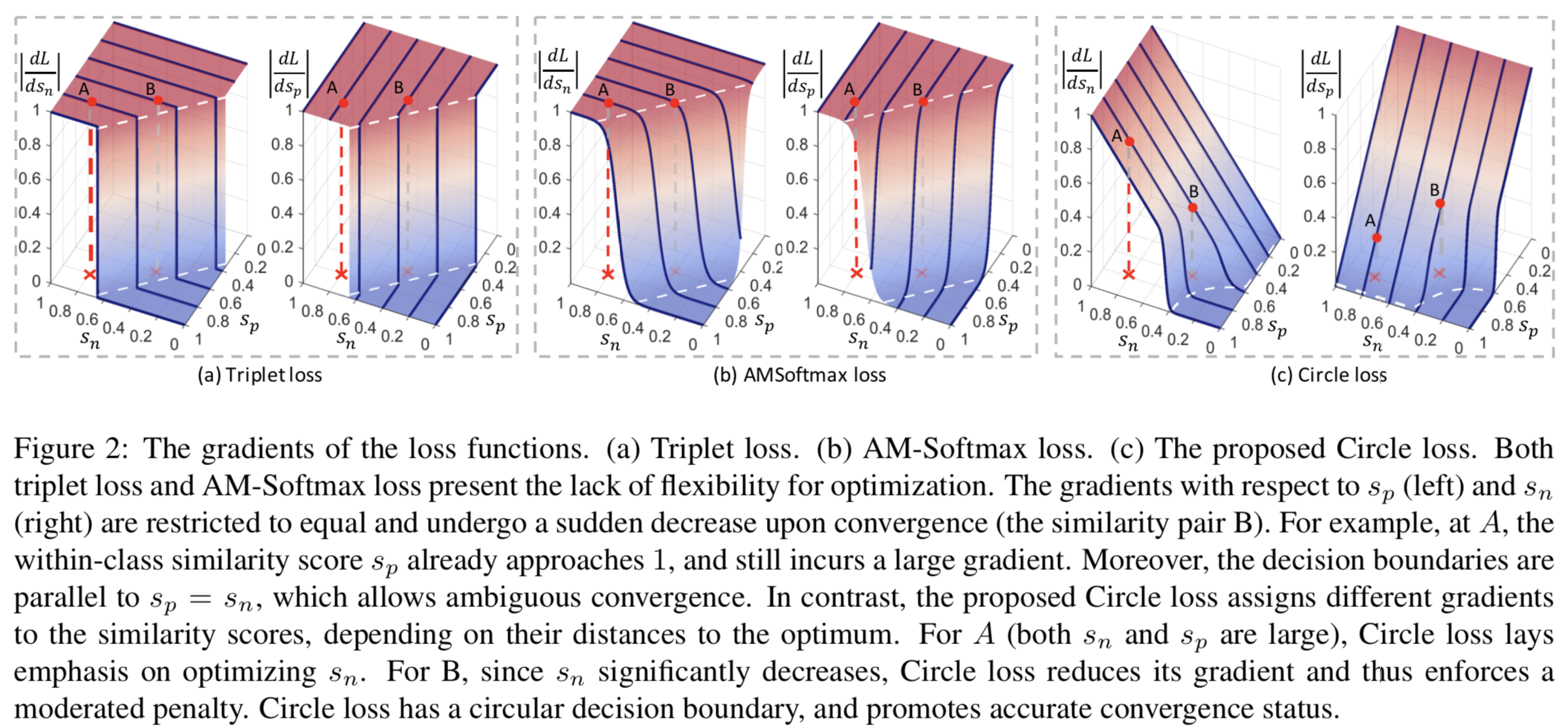
- 首先,在损失达到决策边界(梯度消失)之前,sp和sn的梯度是相同的。状态A有{sn, sp} ={0.8, 0.8},表示类内是紧凑的。但是A的sp仍然有较大的梯度,导致优化时缺乏灵活性。
- 其次,梯度在收敛前保持(大致)不变,收敛后突然下降。状态B更接近于决策边界,并且比A优化得更好。然而,损失函数(包括triplet损失和AM-Softmax损失)对A和B执行了近似相等的惩罚。这是另一个缺乏灵活性的证据。
- 最后,决策边界(白色虚线)
 与
与 平行。边界上任意两点(如图1中的T和T')有着相等的m大小的相似度gap,因此,实现起来也同样困难。从另一方面说来,为了收敛,损失函数最小化
平行。边界上任意两点(如图1中的T和T')有着相等的m大小的相似度gap,因此,实现起来也同样困难。从另一方面说来,为了收敛,损失函数最小化 时,对T和T'并没有任何偏好,倾向于模糊收敛。该问题的实验证明可见第4.6节。
时,对T和T'并没有任何偏好,倾向于模糊收敛。该问题的实验证明可见第4.6节。
这些问题源于最小化(sn−sp)的优化方式,减少sn等价于增加sp。在接下来的第3节中,我们将把这种优化方式转化为更一般的优化方式,以提高灵活性。
3. A New Loss Function
3.1. Self-paced Weighting
我们考虑通过允许每个相似度分数以自己的速度去学习来增强优化灵活性,速度取决于其当前的优化状态。我们首先忽略等式(1)中的边际项m,将统一的损失函数转化为所提出的Circle loss:

其中![]() 和
和![]() 是非负的加权因子
是非负的加权因子
等式(4)源自等式(1),将![]() 转换成
转换成![]() 。在训练中,当后向传播到
。在训练中,当后向传播到![]() 时,
时,![]() 的梯度将乘以
的梯度将乘以![]() 。当相似度分数偏离最优值时(即
。当相似度分数偏离最优值时(即![]() 的
的![]() 和
和![]() 的
的![]() ),其应该得到一个大的加权因子以使用大的梯度得到有效的更新。总之,我们以self-paced的方式定义
),其应该得到一个大的加权因子以使用大的梯度得到有效的更新。总之,我们以self-paced的方式定义![]() 和
和![]() :
:

其中![]() 是"截止为0"操作(即小于0的数则设置为0),以保证
是"截止为0"操作(即小于0的数则设置为0),以保证![]() 和
和![]() 是非负的
是非负的
Discussions. 在监督下对余弦相似度进行再缩放是现代分类损失的一种常见做法[21,30,29,32,39,40]。通常,所有相似分数共享一个相等的缩放因子γ。当我们把分类损失函数中的softmax值视为样本属于某个类别的概率时,等量再缩放是很自然的。相反,Circle loss在再缩放之前,将每个相似度分数与一个独立的加权因子相乘。因此,它摆脱了等量再缩放的限制,允许更灵活的优化。除了更好的优化的好处之外,这种重新加权(或再缩放)策略的另一个重要意义涉及到潜在的解释。Circle loss放弃了用大概率将样本分类到目标类别的解释。相反,它持有相似对优化的观点,其可兼容两种学习范式。
3.2. Within-class and Between-class Margins
在损失函数优化![]() 中添加一个边际m来增强优化效果 [15, 16, 29, 32]。由于sn和−sp处于对称位置,所以sn的正边际相当于sp的负边际,因此只需要一个边际m。在Circle loss中,sn和sp处于不对称位置。自然,sn和sp需要各自的边际值,公式为:
中添加一个边际m来增强优化效果 [15, 16, 29, 32]。由于sn和−sp处于对称位置,所以sn的正边际相当于sp的负边际,因此只需要一个边际m。在Circle loss中,sn和sp处于不对称位置。自然,sn和sp需要各自的边际值,公式为:

其中![]() 和
和![]() 分别为类间和类内边际。
分别为类间和类内边际。
基本上,等式(6)的Circle loss期待![]() 和
和![]() 。我们通过推导决策边界来进一步分析
。我们通过推导决策边界来进一步分析![]() 和
和![]() 的设置。为了简化,我们考虑二分类的情况,其决策边界为
的设置。为了简化,我们考虑二分类的情况,其决策边界为![]() 。与等式(5)结合,决策边界为:
。与等式(5)结合,决策边界为:
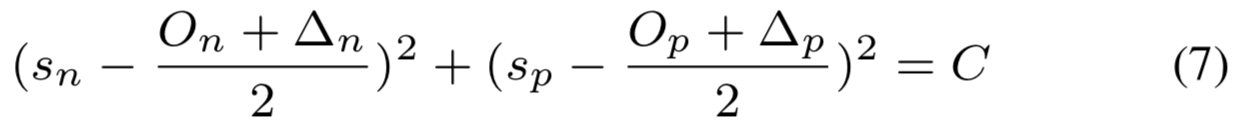
其中![]()
等式(7)表明决策边界为圆弧,如图1(b)所示。圆的中心为![]() ,半径为
,半径为![]()
Circle loss中有5个超参数,即等式(5)中的![]() 和
和![]() ,以及等式(6)中的
,以及等式(6)中的![]() 、
、![]() 和
和![]() 。我们通过设置
。我们通过设置![]() 和
和![]() 来减少超参数的数量。最后,等式(7)的决策边界为:
来减少超参数的数量。最后,等式(7)的决策边界为:
![]()
根据等式(8)中定义的决策边界,我们对Circle loss有了另一种直观的解释。其目的是优化sp→1和sn→0。参数m控制着决策边界的半径,可以看作是一个松弛因子。另一种说法则是Circle loss期望![]() 。
。
因此,现在仅有两个超参数,即缩放因子![]() 和松弛边际m。我们将在第4.5节分析m和
和松弛边际m。我们将在第4.5节分析m和![]() 的影响。
的影响。
3.3. The Advantages of Circle Loss
Circle loss关于![]() 和
和![]() 的梯度可以如下推导得到:
的梯度可以如下推导得到:
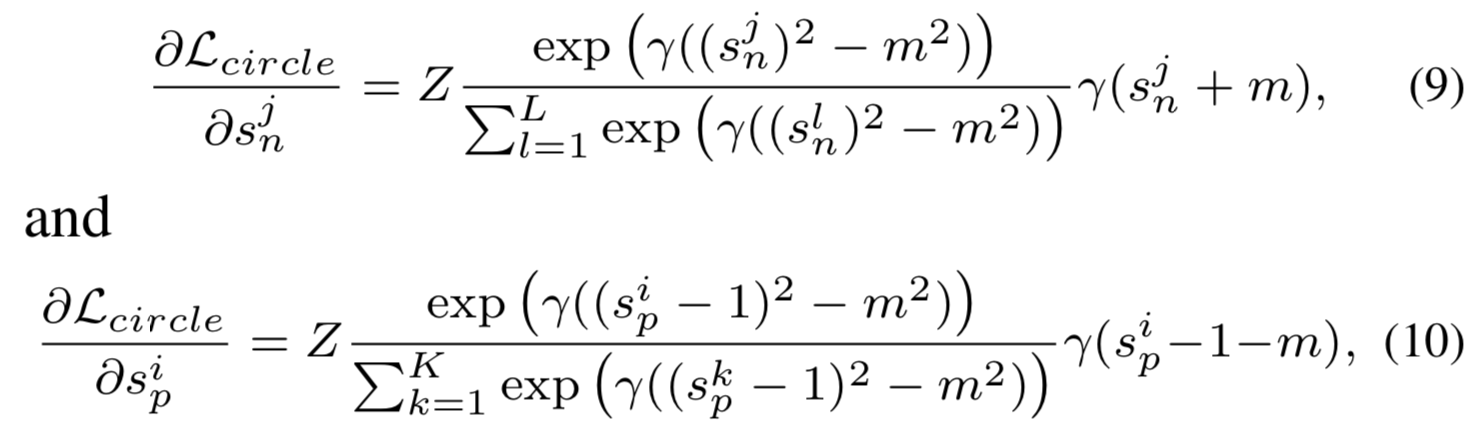
其中![]()
在二分类的toy场景下(或者只有一个sn和sp时),我们在图2 (c)中可视化在不同m设置下的梯度,从中我们得到以下三个观察结果:
Balanced optimization on sn and sp. 我们回想一下,损失函数最小化(sn−sp)在sp和sn上总是有相同的梯度,并且是不灵活的。而Circle loss则呈现出动态的惩罚强度。在指定的相似对{sn, sp}中,如果sp比sn优化得更好(如图2 (c)中A ={0.8, 0.8}),则Circle loss会给sn分配更大的梯度(反之亦然),从而以更高的优先级减小sn。均衡优化的实验证据将在4.6节中给出。
Gradually-attenuated gradients. 在训练开始时,相似度分数偏离最优值,并获得较大的梯度(如图2 (c)中的“A”)。随着训练逐渐趋于收敛,相似度分数上的梯度也相应衰减(如图2 (c)中的“B”),进行比较温和的优化。4.5节的实验结果表明,![]() 设置为任何值,其学习效果都是鲁棒的(在等式(6)中),我们将其归因于自动衰减的梯度。
设置为任何值,其学习效果都是鲁棒的(在等式(6)中),我们将其归因于自动衰减的梯度。
A (more) definite convergence target. Circle loss有一个圆的决策边界,在收敛时其更倾向于T而不是T'(图1)。这是因为与决策边界上的其他点相比,T的sp与sn之间的间隙最小。也就是说,T'在sp和sn之间的间隙更大,本身就更难以维持。而最小化(sn−sp)的损失具有均匀的决策边界,即决策边界上的每个点都具有相同的到达难度。通过实验,我们观察到Circle loss导致收敛后的相似度分布更加集中,具体见4.6节和图5。
4. Experiments
我们综合评估了两种基本的学习方法,即使用class-level标签学习和使用pair-wise标签学习下的Circle loss的有效性。对于前一种方法,我们在人脸识别(第4.2节)和行人再识别(第4.3节)任务上评估了我们的方法。对于后一种方法,我们使用细粒度图像检索数据集(第4.4节),这些数据集相对较小,鼓励使用pair-wise标签进行学习。我们证明了在这两种设置下Circle loss是可行的。第4.5节分析了两个超参数的影响,即等式(6)中的缩放因子![]() 和等式(8)中的松弛因子m。我们证明了在合理的设置下,Circle loss是鲁棒的。最后,第4.6节实验验证了Circle loss的特性。
和等式(8)中的松弛因子m。我们证明了在合理的设置下,Circle loss是鲁棒的。最后,第4.6节实验验证了Circle loss的特性。
4.1. Settings
Face recognition. 我们使用流行的数据集MS-Celeb-1M[4]进行训练。原生的MS-Celeb-1M数据是有噪声的,并且具有长尾数据分布。我们清理脏样本,并排除少数tail身份(即每个身份≤3个图像)。它会产生360万张图片和79.9K的身份信息。采用Megaface Challenge 1 (MF1)[12]、IJB-C[17]、LFW[10]、YTF[37]和CFP-FP[23]数据集进行评估,并采用官方评估协议。在[2]之后,我们还在MF1上改进了probe集和1M干扰物,以便进行更可靠的评估。对于数据预处理,我们将对齐后的人脸图像大小调整为112 × 112,将RGB图像的像素值线性归一化为[−1,1][36,15,32]。我们只通过随机水平翻转来增强训练样本。我们选择流行的残差网络[6]作为我们的backbone。所有的模型都经过182k次迭代训练。学习率从0.1开始,分别在总迭代次数的50%、70%和90%处降低10倍。如果没有指定,我们方法的默认超参数是![]() = 256,m = 0.25。对于所有的模型推理,我们提取512维特征嵌入,并使用余弦距离作为度量。
= 256,m = 0.25。对于所有的模型推理,我们提取512维特征嵌入,并使用余弦距离作为度量。
person re-identification. 人的再识别(re-ID)的目的是在不同的观察中发现同一个人的出现。我们在两个流行的数据集上评估我们的方法,即Market-1501[41]和MSMT17[35]。Market-1501包含1,501个身份,12,936张训练图像和19,732张gallery图像,这些图像是用6台相机拍摄的。MSMT17包含4101个身份,126411个图像,这些图像是用15个摄像头进行捕捉的,并呈现长尾样本分布。我们采用了两种网络结构,即以ResNet50为backbone的全局特征学习模型和名为MGN[31]的part特征模型。我们使用MGN是考虑到它的有竞争力的性能和相对简洁的结构。最初的MGN在每个part特征分支上使用Sofmax损失进行训练。为了简单起见,我们的实现将所有部分特性连接到一个单一的特性向量。对于Circle loss,设![]() = 128, m = 0.25。
= 128, m = 0.25。
Fine-grained image retrieval. 我们使用三个数据集CUB-200-2011[28]、Cars196[14]和Stanford Online Products[19]对细粒度图像检索进行评价。CARS-196包含16,183个图像,它们属于196个汽车类别。前98个类用于训练,后98个类用于测试。CUB-200-2010有200种不同的鸟类。我们使用带有5864张图像的前100个类进行训练,使用带有5924张图像的最后100个类进行测试。SOP是一个大型数据集,包含120,053张图像,属于22,634个在线产品类。训练集包含11,318类,包括59,551张图像,其余11,316类,包括60,499张图像用于测试。实验设置遵循[19]。我们使用BN-Inception[11]作为backbone来学习512维嵌入。我们采用P-K采样策略[8]构造P = 16, K = 5的mini-batch。对于Circle loss,设![]() = 80, m = 0.4。
= 80, m = 0.4。
4.2. Face Recognition
在人脸识别任务中,我们比较了几种常用的分类损失函数,即vanilla Softmax、NormFace[30]、AM-Softmax[29](或CosFace[32])、ArcFace[2]。根据原始文献[29,2],我们AM-Softmax设置为![]() = 64, m = 0.35,ArcFace设置为
= 64, m = 0.35,ArcFace设置为![]() = 64, m = 0.5。
= 64, m = 0.5。
我们在表1中报告了Megaface Challenge 1数据集(MFC1)的识别和验证结果。Circle loss的表现略优于不同backbone下的对照物。例如,以ResNet34为backbone,Circle loss在rank-1 accuracy上超出最具竞争力的对照物(ArcFace)0.13%。以ResNet100为backbone,虽然ArcFace达到了98.36%的rank-1 accuracy,但Circle loss仍然比它高出0.14%。同样的观察结果也适用于验证度量。

表2总结了LFW[10]、YTF[37]、CFP-FP[23]人脸验证结果。我们注意到,这些数据集的性能已经接近饱和。其中ArcFace在三个数据集上分别比AM-Softmax高出0.05%、0.03%、0.07%。Circle loss效果哦仍然是最好的,分别超过ArcFace 0.05%, 0.06%和0.18%。

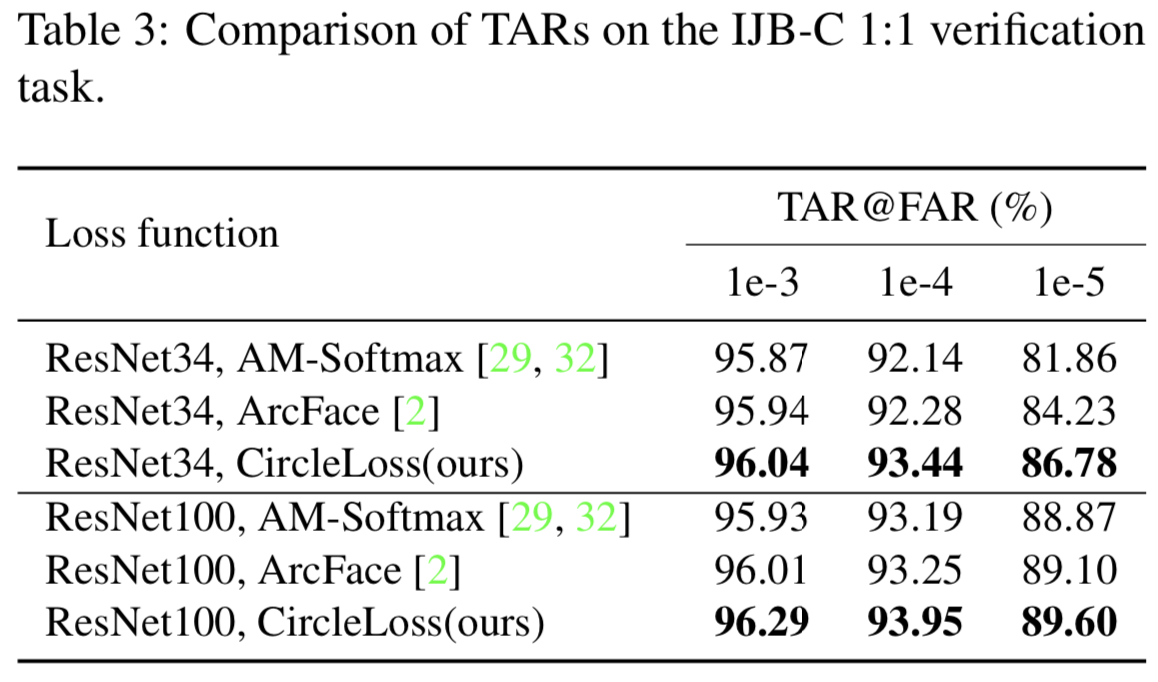
在表3的IJB-C 1:1验证任务中,我们进一步将Circle loss与AM-Softmax和ArcFace进行了比较。在ResNet34和ResNet100 backbone下,Circle loss都表现出相当的优越性。例如,使用ResNet34,在“TAR@FAR=1e-4”和“TAR@FAR=1e-5”上的Circle loss显著高过ArcFace 1.16%和2.55%。
4.3. person Re-identification
我们在表4中评估了re-ID任务上的Circle loss。MGN[31]是最先进的方法之一,用于学习多粒度的part-level特征。最初,它同时使用Softmax损失和triplet损失,以实现joint优化。为了简化,我们的“MGN (ResNet50)+ AM-Softmax”和“MGN (ResNet50)+ Circle loss”的实现只使用了一个单一的损失函数。
我们从表4中得出三个结论。首先,我们发现,Circle loss可以得到能与最先进的方法竞争的再识别准确性。我们注意到在MSMT17[35]上“JDGL”略高于“MGN +Circle loss”。JDGL[42]使用生成模型来扩充训练数据,并显著改善长尾数据集的re-ID。其次,将Circle loss与AM-Softmax进行比较,观察Circle loss的优越性,这与人脸识别任务的实验结果一致。第三,对比“ResNet50 + Circle loss”和“MGN + Circle loss”,我们发现怕恶 level特征对Circle loss有渐进的改善。这意味着Circle loss与专为re-ID设计的part模型是兼容的。

4.4. Fine-grained Image Retrieval
我们在三个细粒度图像检索数据集CUB-200-2011、Cars196和Standford Online Products上评估Circle loss与pair-wise标记数据的兼容性。在这些数据集上,大多数方法[19,18,3,20,13,34]采用鼓励设置pair-wise标签的学习。我们在表5中比较了这些最先进的方法的Circle loss。我们观察到,在所有三个数据集上,Circle loss获得了具有竞争力的性能。在这些方法中,LiftedStruct[19]和Multi-Simi[34]是专门设计的用于pair-wise标签学习的方法,其带有复杂的hard mining策略。HDC[18]、ABIER[20]、ABE[13]受益于模型集成。相比之下,提出的Circle loss能达到与当前最先进的方法同级别的性能。

4.5. Impact of the Hyper-parameters
我们分析了两个超参数,即等式(6)中的缩放因子![]() 和等式(8)中的松弛因子m对人脸识别任务的影响。
和等式(8)中的松弛因子m对人脸识别任务的影响。
缩放因子γ决定了各相似度分数的最大尺度。缩放因子的概念在Softmax损失的许多变体中是至关重要的。我们对其对Circle loss的影响进行了实验评估,并与其他几种涉及缩放因子的损失函数进行了比较。我们将AM-Softmax和Circle loss的![]() 从32变到1024。对于ArcFace,我们只将
从32变到1024。对于ArcFace,我们只将![]() 设置为32、64和128,因为在我们的实现中
设置为32、64和128,因为在我们的实现中![]() 越大,它就变得不稳定。结果如图3所示。与AM-Softmax和ArcFace相比,Circle loss对
越大,它就变得不稳定。结果如图3所示。与AM-Softmax和ArcFace相比,Circle loss对![]() 具有较高的鲁棒性。梯度的自动衰减是Circle loss对
具有较高的鲁棒性。梯度的自动衰减是Circle loss对![]() 鲁棒的主要原因。随着训练过程中相似度分数趋近最优值,加权因子将逐渐减小。因此,梯度会自动衰减,以此得到适度的优化。
鲁棒的主要原因。随着训练过程中相似度分数趋近最优值,加权因子将逐渐减小。因此,梯度会自动衰减,以此得到适度的优化。

松弛因子m决定了圆形决策边界的半径。我们将m设为−0.2 ~ 0.3(区间为0.05),结果如图3 (b)所示。可以看到,在−0.05 ~ 0.25的所有设置下,Circle loss都超过了Arcface和AM-Softmax的最佳性能,表现出相当程度的鲁棒性。
4.6. Investigation of the Characteristics
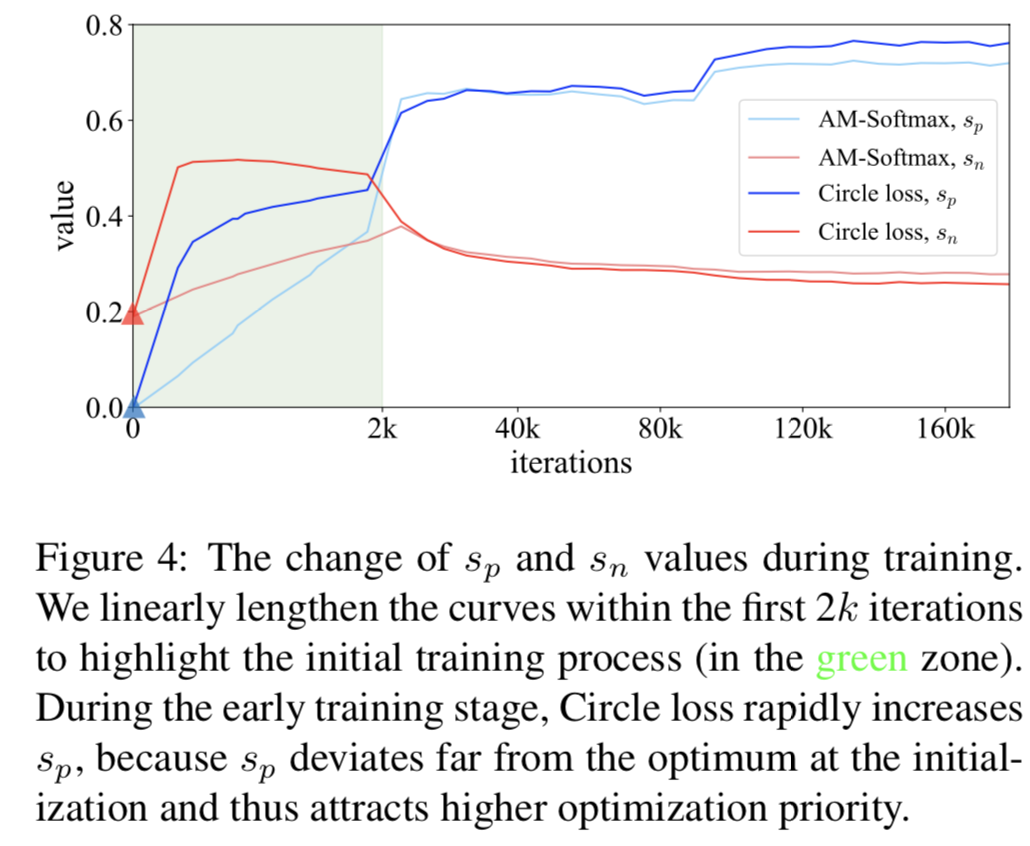
Analysis of the optimization process. 为了直观的了解学习过程,我们在图4中展示了sn和sp在整个训练过程中的变化,从中我们得到了两个观察结果:
首先,在初始化时,所有的sn和sp分数都很小。这是因为随机化的特征在高维特征空间中容易彼此相距很远[40,7]。相应地,sp得到的权重(相对于sn)显著增大,对sp的优化在训练中占主导地位,相似值快速增加,如图4所示。这一现象表明,Circle loss保持了一种灵活、均衡的优化。
其次,在训练结束时,与AM-Softmax相比,Circle loss在训练集上取得了更好的类内紧凑和类间差异。因为Circle loss在测试集上获得了更高的性能,我们认为这意味着更好的优化。
Analysis of the convergence. 图5中我们分析了Circle loss的收敛状态。我们研究了两个问题:由sn和sp组成的相似对在训练过程中如何跨越决策边界,以及它们收敛后如何在(sn, sp)空间中分布。结果如图5所示。在图5 (a)中,AM-Softmax损失采用m = 0.35的最优设置。在图5 (b)中,Circle loss采用折中设置m = 0.325。(a)和(b)的决策边界彼此相切,可以进行直观的比较。在图5 (c)中,Circle loss采用m = 0.25的最佳设置。将图5 (b)和(c)与图5 (a)进行比较,可以发现Circle loss在决策边界上的通道相对狭窄,收敛分布更加集中(特别是m = 0.25时)。这表明,与AM-Softmax损失相比,Circle loss有利于所有相似对的收敛更加一致。这一现象证实了Circle loss具有更明确的收敛目标,从而促进了特征空间的可分性。

5. Conclusion
本文对深度特征学习的优化过程提供了两个见解。首先,大部分的损失函数,包括triplet损失和流行的分类损失,通过将类间和类内的相似度嵌入到相似对中进行优化。其次,在一个被监督的相似对内,每个相似度分数应根据其与最优相似度的距离不同而得到不同的惩罚强度。根据这些见解得到了Circle loss,从而允许相似性分数以不同的速度学习。Circle loss有利于深度特征学习,优化灵活性高,收敛目标更明确。对于两种基本的学习方法,即使用class-level标签学习和使用pair-wise标签学习,它都有一个统一的公式。在各种深度特征学习任务中,如人脸识别、行人再识别和细粒度图像检索,Circle loss的性能达到了与目前的最先进的技术相当的水平。