函数概念
函数的概念有两个,其一为初中的定义,称为传统定义,其二为高中的定义,称为近代定义。
传统定义:设在某变化过程中有两个变量(x)、(y),如果对于(x)在某一范围内的每一个确定的值,(y)都有唯一确定的值与它对应,那么就称(y)是(x)的函数,(x)叫做自变量。我们将自变量(x)取值的集合叫做函数的定义域,和自变量(x)对应的(y)的值叫做函数值,函数值的集合叫做函数的值域。
近代定义:设(A),(B)都是非空的数集,(f:x→y)是从(A)到(B)的一个对应法则,那么从(A)到(B)的映射(f:A→B)就叫做函数,记作(y=f(x)),其中(x∈A),(y∈B),原象集合(A)叫做函数(f(x))的定义域,象集合(C)叫做函数(f(x))的值域,显然有(Csubseteq B)。
- 对函数概念的理解
函数的两个定义本质是一致的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。这样,就不难得知函数实质是从非空数集A到非空数集B的一个特殊的映射。
概念理解
二、基于对应基础的函数概念的理解[近代定义]
(1)首先需要先搞清楚对应的概念,
关于对应的概念,我们基于蜜蜂采蜜的生活常识来理解,可以一只蜜蜂采一朵花(称为“一对一”的对应),
可以一只蜜蜂采多朵花(称为“一对多”的对应),还可以多只蜜蜂采一朵花(称为“多对一”的对应)
即对应有一对一,一对多和多对一三种对应关系。
(2)映射
能够称为映射的对应只有一对一和多对一两种,其中一对多不能称为映射,
映射(f:A ightarrow B)和映射(f:B ightarrow A)是不一样的。
集合(A,B)不一定是数集,可以是图形集,式集,点集,向量集等,
(3)函数
非空数集(A)到非空数集(B)的映射(f:A ightarrow B)就称为函数,记为(y=f(x))。
- 符号(y=f(x))即是“(y)是(x)的函数”的数学表示,
应理解为:(x)是自变量,它是法则所施加的对象;(f)是对应法则,它可以是一个或几个解析式,可以是图象、表格,也可以是文字描述;
(y)是自变量的函数,当(x)为允许的某一具体值时,相应的(y)值为与该自变量值对应的函数值,
当(f)用解析式表示时,则解析式为函数解析式。(y=f(x))仅仅是函数符号,不是表示“(y)等于(f)与(x)的乘积”,
(f(x))也不一定是解析式,在研究函数时,除用符号(f(x))外,还常用(g(x)),(F(x)),(G(x))等符号来表示。
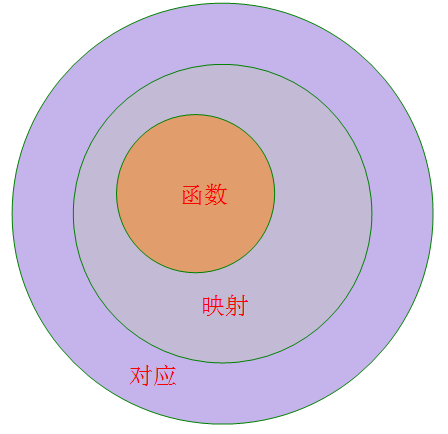
(4)映射与函数的关系:
由关系图可以看出,函数是映射的特殊情况,映射是函数的拓展和推广。
函数是特殊的映射,比如(f:A ightarrow B),其特殊性有以下两点:
①函数是从非空数集(A)到非空数集(B)的映射;
②集合(B)中的每一个元素都有原像,所以(A)是定义域,(B)是值域。
典例剖析
分析:由函数的概念可知,从非空数集到非空数集的映射中,一对一和多对一的映射能上升为函数,但是一对多的映射不能上升为函数,体现在形上,即直线(x=a)((a)为常数)与函数(y=f(x))的图像有(0)个或(1)个交点,故本题目就是用数学语言刻画的这个意思,故本题选(C)。
给定集合(A={1,2,3}),集合(B={a,b,c,d}) ,求映射(f:A ightarrow B)的个数和映射(f:B ightarrow A)的个数。
分析:依据映射的概念,映射(f:A ightarrow B)需要给集合(A)中的每一个元素(原像),都找一个确定的对应对象(像)。
此时注意,原像必须有与之对应的唯一的像,但是像不一定必须有原像和她对应。
我们分步完成:先给元素(1)分配对象,每次取一个有(a、b、c、d)四种选择;
再给元素(2)分配对象,每次取一个也有(a、b、c、d)四种选择;
最后给元素(3)分配对象,每次取一个也有(a、b、c、d)四种选择,
允许出现元素(1、2、3)都对应到元素(a)上而其他元素没有原像与之对应的情形出现;
利用乘法原理,映射(f:A ightarrow B)共有(4 imes 4 imes4=4^3)个,即((cardB)^{cardA})个。
同理,映射(f:B ightarrow A)共有(3^4)个,即((cardA)^{cardB})个。
给定集合(A={1,2,3}),集合(B={a,b,c}) ,求一一映射(f:A ightarrow B)的个数和一一映射(f:B ightarrow A)的个数。
先分析一一映射(f:A ightarrow B)的个数,由于是一一映射,类似有3人坐3个凳子,故有(A_3^3=6)个。
同理,一一映射(f:B ightarrow A)的个数也是(6)种。