前言
数列是特殊的函数,则数列在考查时,完全可能考查其周期性或单调性,本博文主要探究数列的周期性。数列的周期性体现为其一为数列的项的周期性;其二为某几项的和的周期性;
函数周期性
1、(f(x+4)=f(x))或者(f(x+2)=f(x-2)Longrightarrow T=4) 详细推导
2、(f(x+a)=-f(x)Leftrightarrow f(x+a)+f(x)=0Longrightarrow T=2a)
3、(f(x+a)=b-f(x)Leftrightarrow f(x+a)+f(x)=bLongrightarrow T=2a)
4、(f(x+a)=cfrac{k}{f(x)}(k eq 0)Leftrightarrow f(x+a)f(x)=k Longrightarrow T=2a);
5、(f(x+2)=f(x+1)-f(x)Longrightarrow f(x+3)=-f(x)Longrightarrow T=6)
6、(f(x+6)=f(x)+f(3)),且(f(x))为偶函数,(Longrightarrow T=6)(赋值法)
7、(f(x+6)=f(x)+nf(3)(nin N^*)),且(f(x))为偶函数,(Longrightarrow T=6)(赋值法)
数列周期性
务必注意:数列是特殊的函数,(a_n=f(n)),透彻理解这句话的内涵;
- (a_{n+2}=a_n)或(a_{n+2}-a_n=0);则数列的(T=2);
分析:类比(f(n+2)=f(n)),再类比(f(x+2)=f(x));
- (a_{n+2}=-a_n)或 (a_{n+2}+a_n=0);则数列的(T=4);
分析:类比(f(n+2)=-f(n)),再类比(f(x+2)=-f(x));
- (a_{n+2}=cfrac{k}{a_n})或(a_{n+2}cdot a_n=k);(k)为常数;等积数列,则数列的(T=4);
分析:类比(f(n+2)=cfrac{k}{f(n)}),再类比(f(x+2)=cfrac{k}{f(x)}),;
- (a_{n+2}=a_{n+1}-a_n)或(a_{n+2}+a_n=a_{n+1});则数列的(T=6);
分析:类比(f(n+2)=f(n+1)-f(n)),再类比(f(x+2)=f(x+1)-f(x));
-
(a_{n+1}=(-1)^n(a_n+1));通过计算得到周期;
-
由(a_n+a_{n-1}=4(nge 2)),数列的周期为(T=2);
分析:构造(a_{n+1}+a_n=4),两式做差,得到(a_{n+1}-a_{n-1}=0),即数列的周期为(T=2);
典例剖析
法1:利用递推关系推导出数列的前有限项,周期自然就知道了。
由题目可知(a_1=2,a_2=3,a_3=a_2-a_1=1,a_4=a_3-a_2=-2),
(a_5=a_4-a_3=-3,a_6=a_5-a_4=-1,a_7=a_6-a_5=2),
即(a_7=a_1),周期(T=6),所以(a_{2016}=a_6=-1)
法2:由(a_{n+2}=a_{n+1}-a_n)可得到(a_{n+3}=a_{n+2}-a_{n+1}),两个式子相加,得到
(a_{n+2}=-a_{n-1}),用(n+1)替换(n),得到(a_{n+3}=-a_n),仿上可得
(a_{n+6}=a_{[(n+3)+3]}=-a_{n+3}=-(-a_n)=a_n),故周期(T=6),其余仿上完成。
法1:利用递推关系推导出数列的前有限项,
(a_1=1,a_2=3,a_3=cfrac{a_2}{a_1}=3,a_4=cfrac{a_3}{a_2}=1),
(a_5=cfrac{a_4}{a_3}=cfrac{1}{3},a_6=cfrac{a_5}{a_4}=cfrac{1}{3},a_7=cfrac{a_6}{a_5}=1),
周期(T=6),所以(a_{2016}=a_6=cfrac{1}{3}).
法2:由(a_{n+1}=cfrac{a_n}{a_{n-1}})可得,(a_{n+2}=cfrac{a_{n+1}}{a_n}),
两式相乘得到(a_{n+2}=cfrac{1}{a_{n-1}}),即(a_{n+3}=cfrac{1}{a_n}),
(a_{n+6}=a_{[(n+3)+3]}=cfrac{1}{a_{n+3}}=a_n),
故周期(T=6),其余仿上完成。
分析:由题意,很自然想到本题是考察函数的周期,
所以计算前有限项观察周期,(f_1(2)=1,f_2(2)=0,f_3(2)=2,f_4(2)=1,cdots),
所以周期(T=3),所以(f_{2016}(2)=f_3(2)=2).
法1:令(x=y=0),则有(2f(0)=2f^2(0)),得到(f(0)=0或f(0)=1);
再令(x=1,y=0),则有(2f(1)=2f(1)f(0)),得到(f(0)=1);
又题目已知(f(1)=cfrac{1}{2}),再令(x=1,y=1),则有(f(2)+f(0)=2f(1)f(1)),得到(f(2)=-cfrac{1}{2});
再令(x=2,y=1),则有(f(3)+f(1)=2f(2)f(1)),得到(f(3)=-1);
再令(x=3,y=1),则有(f(4)+f(2)=2f(3)f(1)),得到(f(4)=-cfrac{1}{2});
再令(x=4,y=1),则有(f(5)+f(3)=2f(4)f(1)),得到(f(5)=cfrac{1}{2});
再令(x=5,y=1),则有(f(6)+f(4)=2f(5)f(1)),得到(f(6)=1);
再令(x=6,y=1),则有(f(7)+f(5)=2f(6)f(1)),得到(f(7)=cfrac{1}{2});(cdots)
故周期为(T=6),
(f(0)+f(1)+f(2)+cdots+f(2016))
(=336 imes(f(0)+f(1)+f(2)+f(3)+f(4)+f(5))=0).
【法2】:令(x=y=0),则有(2f(0)=2f^2(0)),得到(f(0)=0或f(0)=1);
再令(x=1,y=0),则有(2f(1)=2f(1)f(0)),得到(f(0)=1);
又题目已知(f(1)=cfrac{1}{2}),令(y=1),则有(f(x+1)+f(x-1)=2f(x)f(1)=f(x)),
即就是(f(x+1)+f(x-1)=f(x)),
由此得到(f(x+2)+f(x)=f(x+1)),两式相加得到(f(x+2)=-f(x-1)),
即(f(x+3)=-f(x)),故周期为(T=6),
接下来只要计算(f(2)=-cfrac{1}{2},f(3)=-1,f(4)=-cfrac{1}{2},f(5)=cfrac{1}{2})的值即可,
说明:若令(x=0),则得到(f(y)+f(-y)=2f(0)f(y)=2f(y)),所以(f(-y)=f(y)),可知函数是偶函数。
分析:本题目考查数列的单调性,由(a_n+a_{n+1}+a_{n+2}=4),
得到(a_{n+1}+a_{n+2}+a_{n+3}=4),两式相减得到,(a_{n+3}=a_n),故(T=3),
又由(a_{202}+a_{203}+a_{204}=4),(a_{202}=1),及(a_{203}-a_{204}=1),得到(a_{203}=2),
又(a_{202}=1),故(a_{201}=1),(a_{200}=2),(a_{199}=1),又(200=66 imes 3+2),
则有(S_{200}=66(a_1+a_2+a_3)+a_{199}+a_{200}=66 imes 4+2+1=267)。
分析:带有((-1)^n)的数列更多的体现出周期性,所以计算其前几项发现:
(a_1=1),(a_2=-2),(a_3=-1),(a_4=0),(a_5=1),(a_6=-2),(cdots),
即周期(T=4),且有(a_1+a_2+a_3+a_4=-2),
故(S_{2018}=504 imes(-2)+a_1+a_2=-1008+1-2=-1009).
分析:本题目考查数列的周期性和分组求和;由于(a_1=1),(a_2=-2),(a_3=-3),(a_4=4),(a_5=5),(a_6=-6),(a_7=-7),(a_8=8),(cdots),
观察发现,(a_1+a_2+a_3+a_4=a_5+a_6+a_7+a_8=cdots=a_{2013}+a_{2014}+a_{2015}+a_{2016}=0),且(a_{2017}=2017),(a_{2018}=-2018),(a_{2019}=-2019),
所以(S_{2019}=0 imes cfrac{2016}{4}+2017-2018-2019=-2020)。
法2:思路提示,(a_n=n(sincfrac{npi}{2}+coscfrac{npi}{2})=ncdot sincfrac{npi}{2}+ncdot coscfrac{npi}{2}=b_n+c_n),
然后分析数列({b_n})和({c_n}),
得到(b_{4k+1}+b_{4k+2}+b_{4k+3}+b_{4k+4}=-2),
(c_{4k+1}+c_{4k+2}+c_{4k+3}+c_{4k+4}=2),
故(a_{4k+1}+a_{4k+2}+a_{4k+3}+a_{4k+4}=0),其余同上;
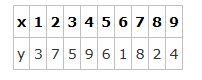
数列({x_n})满足:(x_1=1),且对于任意的(nin N_*),点((x_n,x_{n+1}))都在函数(y=f(x))的图像上,
则(x_1+x_2+cdots+x_{2015}=?)
分析:这是一个很新颖的数列题目,但是和函数的列表法紧密结合,要顺利解答还需要一定的数学素养。
由题目可知(y=f(x),x_{n+1}=f(x_n),x_1=1),
则有(x_2=f(x_1)=f(1)=3);(x_3=f(x_2)=f(3)=5);(x_4=f(x_3)=f(5)=6);
(x_5=f(x_4)=f(6)=1);(cdots,T=4);
(sumlimits_{k=1}^{2015}{x_k}=503(x_1+x_2+x_3+x_4)+(x_1+x_2+x_3)=503 imes 15+9=7554)