前言
图像法,是高中数学学习中高频使用的一种数学方法。以下内容适合数学基础比较好的高一高二同学或高三学生。
采用案例
注意:本案例采用图像法求解三角函数的值域。求解函数的值域的方法是比较多的,具体方法详见函数的值域。
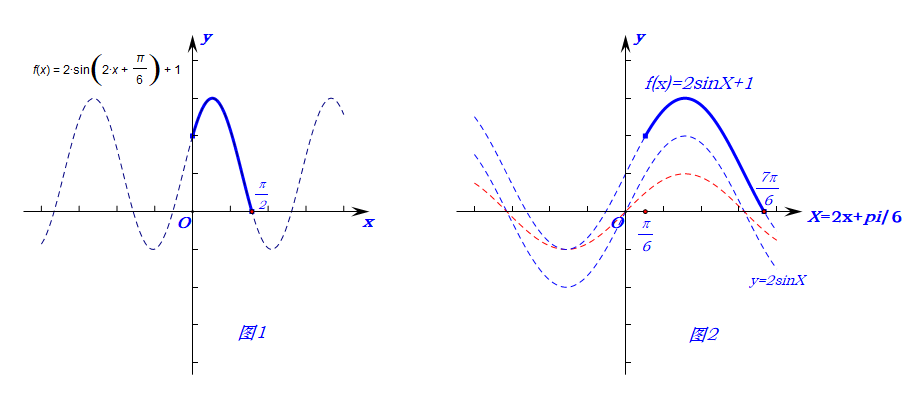
[法1]:横轴为\(x\),如图1所示,利用图像的变换得到函数\(y=2sin(2x+\cfrac{\pi}{6})+1,x\in[0,\cfrac{\pi}{2}]\)的图像,
由图像可以看出来,当\(x=\cfrac{\pi}{2}\)时,函数\(f(x)_{min}=2sin(2\times\cfrac{\pi}{2}+\cfrac{\pi}{6})+1=0\),
当\(x=\cfrac{\pi}{6}\)时,函数\(f(x)_{max}=2sin(2\times\cfrac{\pi}{6}+\cfrac{\pi}{6})+1=3\),
故函数的值域为\([0,3]\)。
[法2]:整体代换,如图2所示,横轴为\(2x+\cfrac{\pi}{6}=X\),
由\(0\leq x\leq \cfrac{\pi}{2}\),故\(\cfrac{\pi}{6}\leq 2x+\cfrac{\pi}{6}\leq \cfrac{7\pi}{6}\),
则\(-\cfrac{1}{2}\leq sin(2x+\cfrac{\pi}{6})\leq 1\),
则\(0\leq 2sin(2x+\cfrac{\pi}{6})+1\leq 3\),
则有 \(0\leq y\leq 3\),函数的值域为\([0,3]\)。[1]
延伸思考
我们在自己的资料上经常会碰到,上述的图像法求解三角函数值域的题目,问题是此时我们常常会忘记深入思考,错失挖掘其中潜在的训练机会。比如暂时能想到的以下的问题:
1、此题目给了两种解法,那么这两种解法的优劣点是什么,为什么;我是否需要都加以学习掌握,考试时我采用哪一种,为什么?
2、此题目的题型:正弦型函数在限定区间上的值域问题;对应的解法:图像法。那么在我学过的函数中,还有哪些函数可以这样求值域?
其实学过的函数都可以这样求值域的,比如 ①一次函数 \(f(x)=2x+3\),\(x\in [-2,5]\);②二次函数 \(g(x)=2x^2+3x+1\),\(x\in [-2,5]\); ③指数函数 \(h(x)=2^x\),\(x\in [-2,2]\); ④对数函数 \(m(x)=log_2x\),\(x\in [-2,2]\);。。。
但新问题又来了,我自己按照这样的方法求解的结果对不对呀,又没有个老师或同学告诉我对错,不着急,这时候你可以用电脑工具验证呀,这样的话,你的数学活动经验不就更多,体验就更深入了吗。
3、以上的问题【具体函数】我都可以解决了,那么我能不能找个抽象的函数来练练手,试一试用图像法求值域;
比如,已知函数 \(f(x)\) 是 \([0,3]\) 上的增函数,\(A(0,-3)\) 是图像上的最低点,\(B(3,1)\)是图像上的最高点,则可知函数的值域为 \([-3,1]\)。
4、你还能自己编写一些这样的题目吗?应用层面;
5、为什么图像法可以求值域,还可以做什么?反思提升
①比如用图像法解不等式;
分析:原不等式即\(-3=f(0)<f(x+1)<f(3)=1\),故得到\(0<x+1<3\),解得\(-1<x<2\),
故其补集为\((-\infty,-1]\cup[2,+\infty)\).
反思总结:
1、从作图角度讲,图2的做法由于使用了整体代换,作图过程简单明了,思路清晰,截取快捷,故常用图2的方法来做三角函数的图像。
2、用图2的方法也可以求解函数的单调区间。比如,对函数\(y=2sinX+1\)而言,在\(X\in [\cfrac{\pi}{6},\cfrac{\pi}{2}]\)上单调递增,即\(2x+\cfrac{\pi}{6}\in [\cfrac{\pi}{6},\cfrac{\pi}{2}]\)上单调递增,解得\(x\in [0,\cfrac{\pi}{6}]\),即函数\(y=2sin(2x+\cfrac{\pi}{6})+1\)在区间\([0,\cfrac{\pi}{6}]\)上单调递增,和图1的单调递增区间是一样的。 ↩︎