探求|线段或棱上是否存在一个点

前言

当在线段上选定了一个动点后，利用线段的比例或利用向量共线，就可以将形的问题转化为数的问题了。比如探究线段 \(PB\) 上是否存在一个点 \(S\)，那么我们就假设存在满足条件的点 \(S\)，可设 \(\overrightarrow{PS}=\lambda\overrightarrow{PB}(0\leqslant\lambda\leqslant 1)\)，则若点 \(S\) 真的存在，则计算后就能得到\(\lambda\) 的值；若点 \(S\) 真的不存在，则计算后就不能得到\(\lambda\) 的值或者方程无解等。这不就是形和数的对应性吗？我们从形上感觉处理不了，转化为数的形式，不就可以计算了吗。

典例剖析

已知四棱锥\(P-ABCD\)中，底面是梯形， \(DC//AB\)，\(AB=BC=2DC=4\)，\(\angle ABC=90^{\circ}\)，\(BD\)与\(AC\)交于点\(F\)，平面\(PDC\perp\)平面\(ABCD\)，\(PD=PC\)，点\(G\)是\(AP\)上一点，且\(AG=2GP\)；

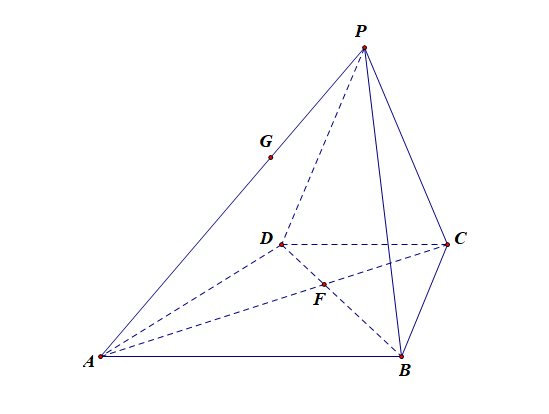
(1).求证: \(GF//\)平面\(PBC\)；

证明: 因为\(DC//AB\)， 所以\(\triangle ABF\sim \triangle CDF\)，则有\(\cfrac{AF}{FC}=\cfrac{AB}{DC}=2\)

又由于\(\cfrac{AF}{FC}=2=\cfrac{AG}{GP}\)，所以 \(GF//PC\)，

又\(GF\not\subset\)平面 \(PBC\)，\(PC\subsetneqq\) 平面 \(PBC\)，所以 \(GF//\)平面 \(PBC\)；

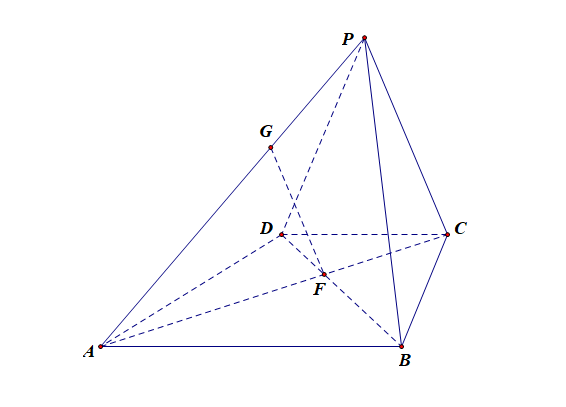
(2). 若二面角 \(P-AB-C\)为 \(45^{\circ}\)，

① 求直线 \(PC\) 与平面 \(PAB\) 所成角的正弦值；

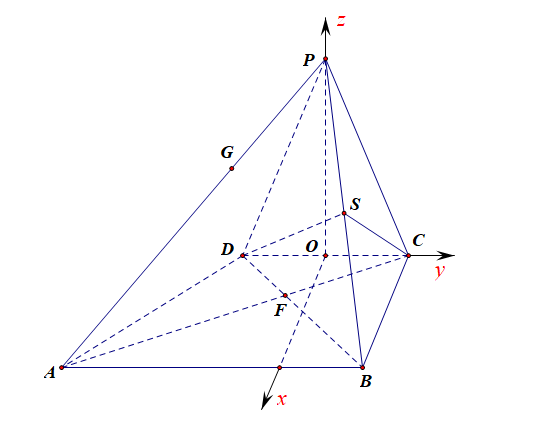
解：取\(DC\)中点 \(O\)，并在平面 \(ABCD\) 内作 \(DC\) 的垂线\(Ox\)，连接 \(OP\)，

由于\(PD=PC\)，所以\(PO\perp DC\)，又因为平面 \(PDC\perp\)平面\(ABCD\)，所以\(PO\perp\)平面 \(ABCD\)，

所以 \(Ox\)、\(OP\) 、 \(OC\)两两垂直，以\(O\)为坐标原点，建立空间直角坐标系\(O-xyz\), 如图所示；

设 \(OP=a(a>0)\)，则\(O(0,0,0)\)， \(A(4,-3,0)\)，\(B(4,1,0)\)， \(C(0,1,0)\)， \(P(0,0, a)\)，

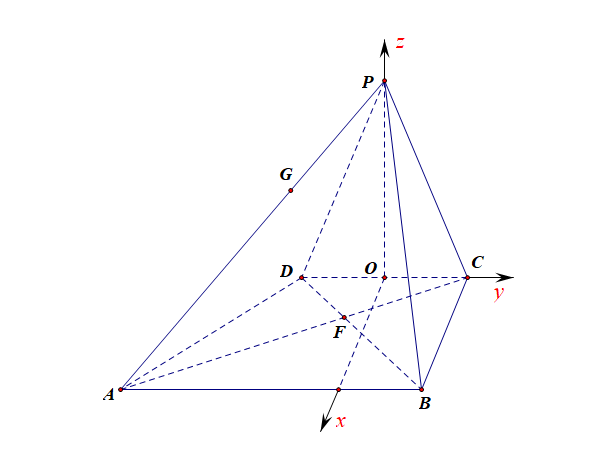
设平面 \(PAB\) 的法向量为\(\vec{m}=(x, y, z)\)，则 \(\vec{m}\perp \overrightarrow{BA}\)， \(\vec{m}\perp\overrightarrow{B P}\);

又\(\overrightarrow{BA}=(0,-4,0)\)，\(\overrightarrow{BP}=(-4,-1, a)\)，

所以\(\left\{\begin{array}{l}{4y=0}\\{-4x-y+az=0}\end{array}\right.\)，解得 \(y=0\), \(z=\cfrac{4}{a}x\)，

令\(x=a\)，则\(y=0\)，\(z=4\)，得 \(\vec{m}=(a, 0,4)\)

则cos \(<\vec{m},\vec{n}>=\cfrac{\vec{m}\cdot\vec{n}}{|\vec{m}|\times|\vec{n}|}=\cfrac{4}{\sqrt{a^{2}+16}}=\cfrac{\sqrt{2}}{2}\)，解得\(a^{2}=16\)，

由\(a>0\)， 则\(a=4\)， 所以点 \(P(0,0,4)\)，

所以\(\cos <\overrightarrow{PC}, \vec{m}>=\cfrac{-16}{\sqrt{17}\times\sqrt{16+16}}=-\cfrac{2\sqrt{34}}{17}\)

设\(PC\)与平面\(PAB\) 所成的角为 \(\theta\)，则\(\theta\in[0,\cfrac{\pi}{2}]\)，

所以\(\sin\theta=|\cos<\overrightarrow{PC},\vec{m}>|=\cfrac{2 \sqrt{34}}{17}\)，

即直线\(PC\)与平面 \(PAB\) 所成角的正弦值为\(\cfrac{2\sqrt{34}}{17}\)；

② 在棱 \(PB\) 上是否存在一点 \(S\)， 使得平面 \(SDC\perp\)平面\(PAB\)？若存在，求出 \(CS\) 的长度； 若不存在， 说明理由.

解析：假设存在满足条件的点 \(S\)，可设 \(\overrightarrow{PS}=\lambda\overrightarrow{PB}(0\leqslant\lambda\leqslant 1)\)，

则 \(\overrightarrow{CS}=\overrightarrow{CP}+\overrightarrow{PS}=\overrightarrow{CP}+\lambda\overrightarrow{PB}=(0,-1,4)+\lambda(4,1,-4)=(4\lambda,\lambda-1,4-4\lambda)\)

设平面\(SDC\)的法向量为 \(\vec{b}=(x, y, z)\)，则\(\vec{b}\perp\overrightarrow{DC}\)，\(\vec{b}\perp \overrightarrow{C S}\)，

又\(\overrightarrow{DC}=(0,4,0)\)，所以\(\left\{\begin{array}{l}{4y=0}\\{4\lambda x+(\lambda-1)y+(4-4\lambda)z=0}\end{array}\right.\)

解得\(y=0\)，\(\lambda x=(\lambda-1)z\)，

令\(z=\lambda\)，\(x=\lambda-1\)，则 \(\vec{b}=(\lambda-1,0,\lambda)\)，

由平面 \(SDC\perp\)平面 \(PAB\)， \(\vec{b}\perp \vec{m}\),

所以 \(4(\lambda-1)+4\lambda=0\)， 解得 \(\lambda=\cfrac{1}{2}\in[0,1]\)，

所以存在满足条件的\(S\)点，且\(S\)为\(PB\)的中点，此时 \(S\) 点坐标为\((2, \cfrac{1}{2}, 2)\)， 且\(CS=\sqrt{4+\cfrac{1}{4}+4}=\cfrac{\sqrt{33}}{2}\).