前言
一般来说,研究三角函数的定义域、值域,单调性,零点,极值点,对称性时,若利用图像法求解,此时横轴可以选\(x\),也可以选 \(\omega x+\phi\)。
典例剖析
其中所有正确结论的编号是【\(\qquad\)】
〔相关储备〕:解题之前,我们先看看动态的图像,区间 \([0,2\pi]\) 是固定不动的,当我们调整 \(\omega\) 时,落在区间 \([0,2\pi]\) 上的零点会发生变化,这时候我们可以动静转换,先做有且仅有\(5\)个零点的三角函数图像,把 \(a\) 与 \(b\) 固定下来,让 \(2\pi\) 运动,这样便于解题;
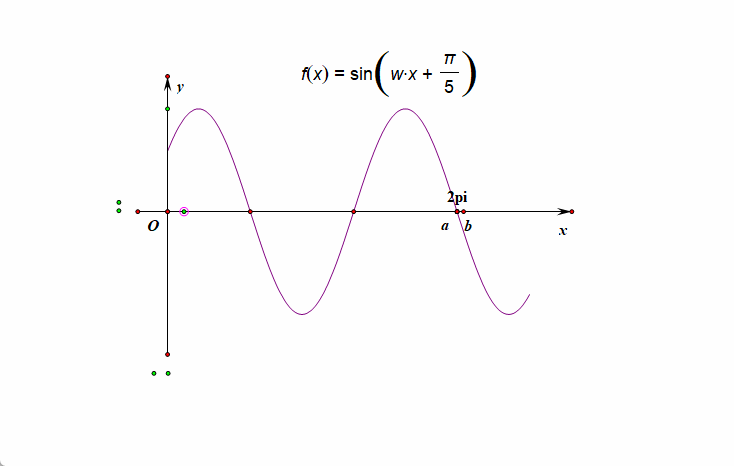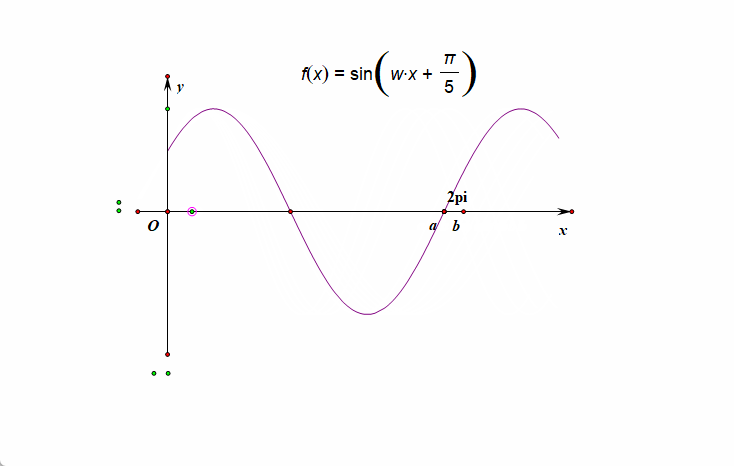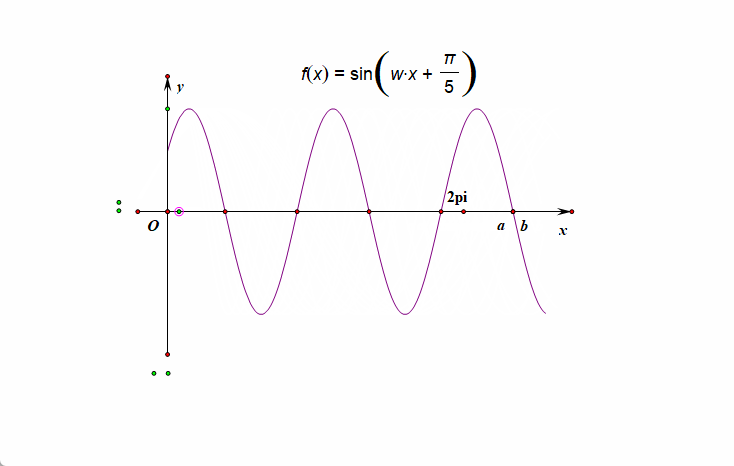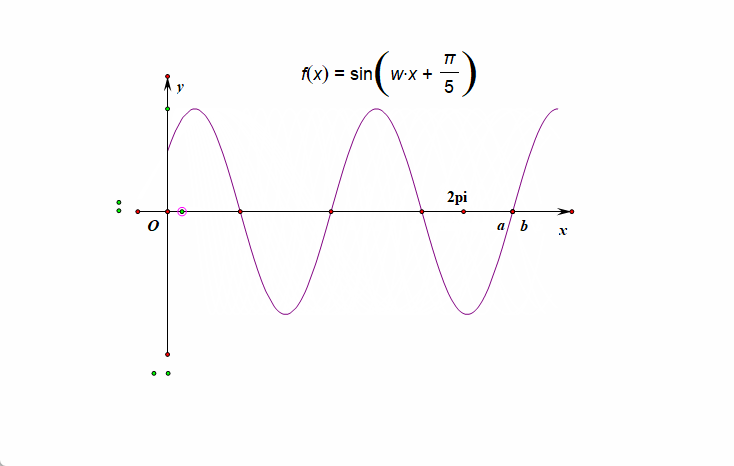
〔解法1〕:以 \(x\) 轴为横轴作图求解;已知\(f(x)=\sin(\omega x+\cfrac{\pi}{5})(\omega>0)\) 在\([0, 2\pi]\) 有且仅有\(5\)个零点,如图此时如何作图呢,我们从 \((0,\sin\cfrac{\pi}{5})\) 开始描点,先做有且仅有\(5\)个零点的三角函数图像,最后将 \(2\pi\) 描在区间 \((a,b)\) 之间[注意此时坐标轴的横坐标为 \(x\) ],
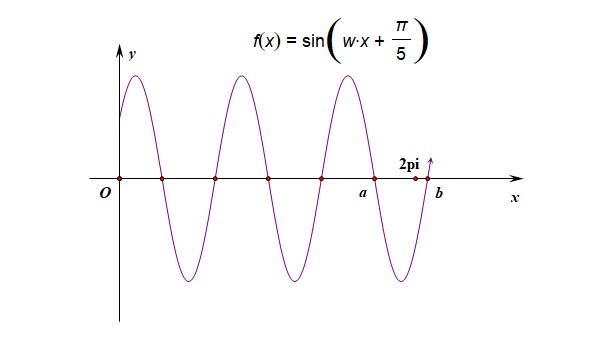
其图像的右端点的横坐标\(2\pi\) 在\([a, b)\)上时,此时 \(f(x)\) 在 \((0,2\pi)\) 有且仅有 \(3\)个极大值点,
但\(f(x)\)在\((0,2\pi)\)可能有\(2\)或\(3\)个极小值点,所以①正确,②不正确;
当\(x\in[0, 2\pi]\)时,\(\omega x+\cfrac{\pi}{5}\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)此时 \(\omega\)\(x\)\(+\)\(\cfrac{\pi}{5}\)的取值区间是变化的,其中区间的左端点固定为 \(\cfrac{\pi}{5}\),右端点为 \(2\pi\omega+\cfrac{\pi}{5}\) 是随 \(\omega\) 的取值变化的。,
由\(f(x)\) 在\([0,2\pi]\)有且仅有\(5\)个零点可得此处,当我们以\(\omega x+\cfrac{\pi}{5}\)为横轴做图像时,要保证有且仅有\(5\)个零点,必须限制右端点满足条件\(5\pi\leqslant 2\pi\omega+\cfrac{\pi}{5}<6\pi\),\(5\pi\leqslant 2\pi\omega+\cfrac{\pi}{5}<6\pi\)
解得\(\omega\)的范围是\([\cfrac{12}{5},\cfrac{29}{10})\),所以④正确;
当\(x\in (0,\cfrac{\pi}{10})\)时,\(\cfrac{\pi}{5}\)\(<\)\(\omega x+\cfrac{\pi}{5}\)\(<\)\(\cfrac{\pi\omega}{10}+\cfrac{\pi}{5}\)此时我们想知道区间 \((\cfrac{\pi}{5}\)\(,\)\(\cfrac{\pi\omega}{10}\)\(+\)\(\cfrac{\pi}{5})\) 是否在函数的单调递增区间 \([-\cfrac{\pi}{2}\)\(,\)\(\cfrac{\pi}{2}]\) 内,从左端点来看,有在函数的单调递增区间的可能性,故重点计算右端点的取值范围;\(<\)\(\cfrac{49\pi}{100}<\cfrac{\pi}{2}\),
[注释:由于\(\omega\in [\cfrac{12}{5},\cfrac{29}{10})\),故\(\cfrac{\pi\omega}{10}+\cfrac{\pi}{5}<\cfrac{\pi}{10}\times \cfrac{29}{10}+\cfrac{\pi}{5}=\cfrac{49\pi}{100}\)]
所以 \(f(x)\) 在 \((0,\cfrac{\pi}{10})\) 单调递增,所以③正确. 故选 \(D\) .
〔解法2〕:以 \(\omega x+\phi\) 为横轴作图求解;此时作图的优越性在于我们可以利用五点法很快做出两到三个周期上的函数简图,起始点一定是从 \((0,0)\) 开始,
当\(x\in[0, 2\pi]\)时,\(\omega x+\cfrac{\pi}{5}\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)此时 \(\omega\)\(x\)\(+\)\(\cfrac{\pi}{5}\)的取值区间是变化的,其中区间的左端点固定为 \(\cfrac{\pi}{5}\),右端点为 \(2\pi\omega+\cfrac{\pi}{5}\) 是随 \(\omega\) 的取值变化的。,
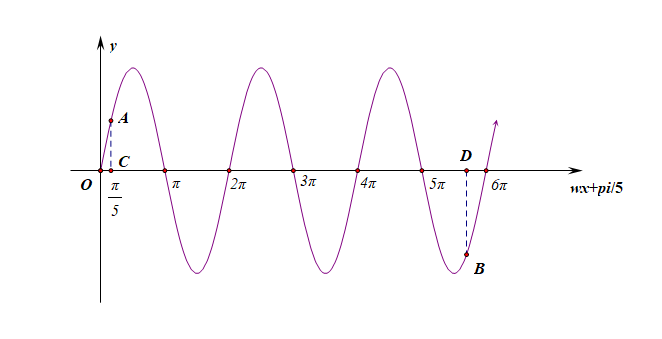
此时的动区间 \([\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\) 对应于横轴上的线段 \(CD\) ,也对应图像中的曲线上的 \(AB\) 之间,
由\(f(x)\) 在\([0,2\pi]\)有且仅有 \(5\) 个零点 对应函数 \(g(x)=\sin x\),在 \(x\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)上有且仅有 \(5\) 个零点,故必须有,\(5\pi\leqslant 2\pi\omega+\cfrac{\pi}{5}<6\pi\),解得\(\omega\)的范围是\([\cfrac{12}{5},\cfrac{29}{10})\),所以④正确;
同理,\(f(x)\) 在 \((0,2\pi)\) 有且仅有 \(3\) 个极大值点对应函数 \(g(x)=\sin x\),在 \(x\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)上有且仅有 \(3\) 个极大值点,由图像看,显然 ① 正确;
而 \(f(x)\) 在 \((0,2\pi)\) 有且仅有 \(2\) 个极小值点对应函数 \(g(x)=\sin x\),在 \(x\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)上有且仅有 \(2\) 个极小值点,由图像看可能有\(2\)或\(3\)个极小值点,显然 ② 错误;
当\(x\in (0,\cfrac{\pi}{10})\)时,\(\cfrac{\pi}{5}\)\(<\)\(\omega x+\cfrac{\pi}{5}\)\(<\)\(\cfrac{\pi\omega}{10}+\cfrac{\pi}{5}\)此时我们想知道区间 \((\cfrac{\pi}{5}\)\(,\)\(\cfrac{\pi\omega}{10}\)\(+\)\(\cfrac{\pi}{5})\) 是否在函数的单调递增区间 \([-\cfrac{\pi}{2}\)\(,\)\(\cfrac{\pi}{2}]\) 内,从左端点来看,有在函数的单调递增区间的可能性,故重点计算右端点的取值范围;\(<\)\(\cfrac{49\pi}{100}<\cfrac{\pi}{2}\),
[注释:由于\(\omega\in [\cfrac{12}{5},\cfrac{29}{10})\),故\(\cfrac{\pi\omega}{10}+\cfrac{\pi}{5}<\cfrac{\pi}{10}\times \cfrac{29}{10}+\cfrac{\pi}{5}=\cfrac{49\pi}{100}\)]
所以 \(f(x)\) 在 \((0,\cfrac{\pi}{10})\) 单调递增,所以③正确. 故选 \(D\) .
〔解后反思〕:为什么可以利用解法2来求解,是因为函数 \(y=f(x)=\sin(\omega x+\cfrac{\pi}{5})\)\((\omega>0)\),\(x\in[0,2\pi]\) 的图像等价于函数 \(g(t)=\sin t\),\(t\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)的图像,显然解法2要简单一些,而且解法统一;
对应练习
①.当 \(a=0\) 时, \(\omega\) 的取值范围是 \([\cfrac{17}{7}, \cfrac{23}{7})\);
②.当 \(a=0\) 时, \(f(x)\) 在 \([0, \cfrac{7\pi}{6}]\) 上恰有 \(2\) 个极小值点和 \(1\) 个极大值点;
③.当 \(a=0\) 时, \(f(x)\) 在 \([0, \cfrac{\pi}{12}]\) 上单调递增;
④.当 \(\omega=2\) 时, \(a\) 的取值范围为 \([\cfrac{1}{2}, 1)\), 且 \(x_{1}+2 x_{2}+x_{3}=\cfrac{5\pi}{3}\).
其中正确的结论为___________(填序号).
解析:仿上例中的法2,以 \(\omega x+\phi\) 为横轴作图求解;
当 \(0 \leqslant x \leqslant \cfrac{7 \pi}{6}\) 时, \(\cfrac{\pi}{6} \leqslant \omega x+\cfrac{\pi}{6} \leqslant \cfrac{7 \omega \pi}{6}+\cfrac{\pi}{6}\),
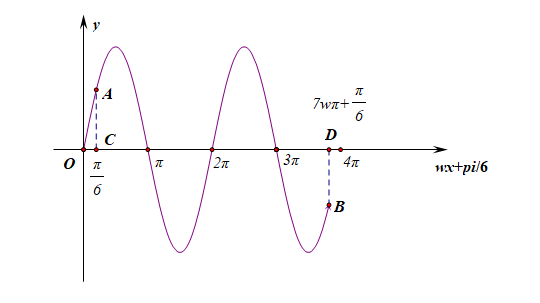
此时图像是曲线中的点 \(A\) 到点 \(B\) 之间的部分,落在横轴上的部分为 \([\cfrac{\pi}{6},\cfrac{7\omega\pi}{6}+\cfrac{\pi}{6}]\),其中点 \(D\) 的横坐标 \(\cfrac{7\omega\pi}{6}+\cfrac{\pi}{6}\) 应该在区间 \([3\pi,4\pi)\) 之间活动,
此时由图像可知,若 \(f(x)\) 恰有 \(3\) 个零点, 则 \(3 \pi \leqslant \cfrac{7 \omega \pi}{6}+\cfrac{\pi}{6}<4\pi\), 解得 \(\cfrac{17}{7} \leqslant \omega<\cfrac{23}{7}\), 故 ① 正确;
且由图可知, \(f(x)\) 在 \([0,\cfrac{7\pi}{6}]\) 上恰有 \(2\) 个极大值点和 \(1\) 个(或 \(2\) 个)极小值点, 故 ② 错误;
当 \(x\in[0,\cfrac{\pi}{12}]\) 时, \(\cfrac{\pi}{6} \leqslant \omega x+\cfrac{\pi}{6} \leqslant \cfrac{\omega \pi}{12}+\cfrac{\pi}{6}\),
由于 \(\cfrac{17}{7} \leqslant \omega<\cfrac{23}{7}\),故 \(\omega x+\cfrac{\pi}{6}\) 的右端点的活动区间为 \(\cfrac{17}{7}\times\cfrac{\pi}{12}+\cfrac{\pi}{6}\)\(\leqslant\)\(\cfrac{\pi\omega}{12}+\cfrac{\pi}{6}\)\(<\)\(\cfrac{23}{7}\times\cfrac{\pi}{12}+\cfrac{\pi}{6}\),
即\(\cfrac{31\pi}{84}\leqslant\)\(\cfrac{\pi\omega}{12}+\cfrac{\pi}{6}<\cfrac{37\pi}{84}<\cfrac{\pi}{2}\),故 \([\cfrac{\pi}{6}, \cfrac{\omega \pi}{12}+\cfrac{\pi}{6}]\subsetneqq[0, \cfrac{\pi}{2}]\),则 \(f(x)\) 在 \([0, \cfrac{\pi}{12}]\) 上单调递增, 故 ③ 正确;
当 \(\omega=2\) 时, \(2x+\cfrac{\pi}{6} \in[\cfrac{\pi}{6}, \cfrac{5\pi}{2}]\), 画出函数的大致图象:
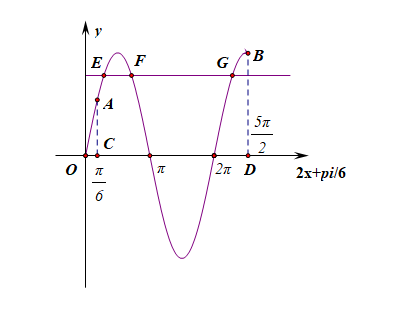
由图可知,要保证 \(f(x)=a\) 有三个交点,则 \(a\) 的取值范围为 \([\cfrac{1}{2}, 1)\),且图上的三个交点 \(E\)、\(F\)、\(G\) 的横坐标应该依次为 \(2x_1+\cfrac{\pi}{6}\), \(2x_2+\cfrac{\pi}{6}\), \(2x_3+\cfrac{\pi}{6}\),[原因是以 \(\omega x+\phi\) 为横轴作图],且点 \(E\)、\(F\) 关于直线 \(x=\cfrac{\pi}{2}\) 对称,点 \(F\)、\(G\) 关于直线 \(x=\cfrac{3\pi}{2}\) 对称,
故由 \((2x_1+\cfrac{\pi}{6})+(2x_2+\cfrac{\pi}{6})=\pi\),解得 \(x_{1}+x_{2}=\cfrac{\pi}{3}\),
由 \((2x_2+\cfrac{\pi}{6})+(2x_3+\cfrac{\pi}{6})=3\pi\),解得 \(x_{2}+x_{3}=\cfrac{4\pi}{3}\),
所以 \(x_{1}+2 x_{2}+x_{3}=\cfrac{5\pi}{3}\), 故 ④ 正确, 故填 ① ③ ④ .