前言
零点分区间讨论法,比如解不等式\((x+1)(x-2)(x+3)>0\),为便于表述令\(P=(x+1)(x-2)(x+3)\),
先找到零点\(x=-3,x=-1,x=2\),然后分区间列表得到
由表格就可以得到不等式的解集\(\{x\mid -3<x<-1\) 或 \(x>2\}\)。
这就是零点分区间讨论法,在解不等式时的应用案例。
典例剖析
(1)当\(a=1\)时,求不等式\(f(x)\ge g(x)\)的解集。
法1:零点分区间讨论法,我们先转化函数\(g(x)\)为分段函数,分别令\(x+1=0\)和\(x-1=0\),得到\(x=-1\)和\(x=1\),这样这两个实数就把数轴分成了三段,分三类情况讨论如下
\(g(x)=\begin{cases}-x-1-x+1,&x\leq -1\\x+1-x+1,&-1<x<1\\x+1+x-1,&x\ge 1\end{cases}\),整理得到\(g(x)=\begin{cases}-2x,&x\leq -1\\2,&-1<x<1\\2x,&x\ge 1\end{cases}\),
当\(a=1\)时,\(f(x)=-x^2+x+4\),则\(f(x)\ge g(x)\)就等价转化为以下三个不等式组:
\(\begin{cases}x\leq -1\\-x^2+x+4\ge -2x\end{cases}\)或者\(\begin{cases}-1< x< 1\\-x^2+x+4\ge 2\end{cases}\)或者\(\begin{cases}x\ge 1\\-x^2+x+4\ge 2x\end{cases}\)
分别解得\(x\leq -1\)或\(-1<x<1\)或\(1\leq x\leq \cfrac{\sqrt{17}-1}{2}\),求其并集得到原不等式的解集为\([-1,\cfrac{\sqrt{17}-1}{2}]\)。

法2:分别作出两个函数的图像,再求得交点,有图像可以直观的看到原不等式的解集为\([-1,\cfrac{\sqrt{17}-1}{2}]\)。
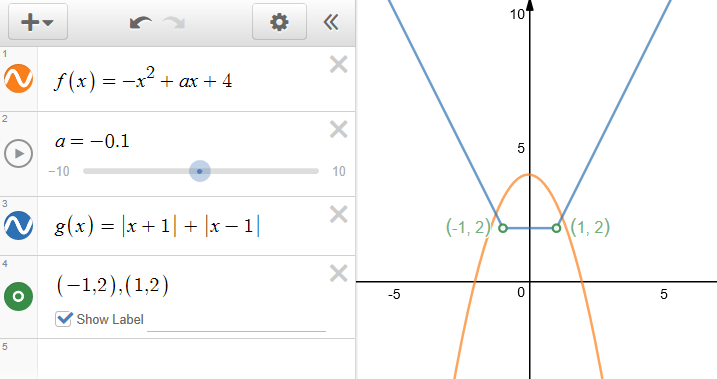
(2)若不等式\(f(x)\ge g(x)\)的解集包含\([-1,1]\),求\(a\)的取值范围。
法1:数形结合法,函数\(f(x)=-x^2+ax+4\),对称轴为\(x=\cfrac{a}{2}\),开口向下,由有图可知,要使得不等式\(f(x)\ge g(x)\)的解集包含\([-1,1]\),只需要满足条件\(\begin{cases}f(-1)\ge 2\\f(1)\ge 2\end{cases}\),解得\(\begin{cases}a\leq 1\\a\ge -1\end{cases}\),故\(a\)的取值范围为\([-1,1]\)。
法2:转化为不等式恒成立求解,当\(x\in [-1,1]\)时,\(g(x)=2\),由题目可知,不等式\(f(x)\ge 2\)的解集包含\([-1,1]\),即当\(x\in [-1,1]\)时,\(f(x)\ge 2\)恒成立,即\(-x^2+ax+2\ge 0\)恒成立,
令\(h(x)=-x^2+ax+2\),则只需满足条件\(\begin{cases}h(-1)\ge 0\\h(x)\ge 0\end{cases}\),解得\(-1\leq a \leq 1\),故\(a\)的取值范围为\([-1,1]\)。
法3:恒成立+分离参数法
当转化得到\(x\in [-1,1]\)时,\(f(x)\ge 2\)恒成立,即\(-x^2+ax+2\ge 0\)恒成立,接下来准备分离参数:
\(1^。\)当\(x=0\)时,代入得到\(2\ge 0\),即\(a\in R\);
\(2^。\)当\(x<0\)时,由\(ax\ge x^2-2\)分离参数得到\(a\leq \cfrac{x^2-2}{x}=x-\cfrac{2}{x}\),令\(h(x)=x-\cfrac{2}{x}\),\(h(x)\)在区间\((-1,0)\)上单调递增,故\(h(x)_{min}\rightarrow h(-1)=1\)即\(a\leq 1\);
\(3^。\)当\(x>0\)时,由\(ax\ge x^2-2\)分离参数得到\(a\ge \cfrac{x^2-2}{x}=x-\cfrac{2}{x}\),令\(h(x)=x-\cfrac{2}{x}\),\(h(x)\)在区间\((0,1)\)上单调递增,故\(h(x)_{max}\rightarrow h(1)=-1\)即\(a\ge -1\);
综上所述,由于三种情形下都要成立,故需要取其交集得到\(a\)的取值范围为\([-1,1]\)。