前言
在我们的求学过程中,老师告诉我们,点是没有大小、没有高度、没有宽度、没有面积、没有体积的,我们也没有怀疑过这一说法。但我们坚信点的多少我们还是能数清楚的,这是真的吗?
案例剖析
我们的生活常识是,线是由点构成的,那么线越长,自然其上的点就越多,所以,半径大的圆上的点自然要更多一些,其实这个认知是错误的,请看下面的动画演示和解释。
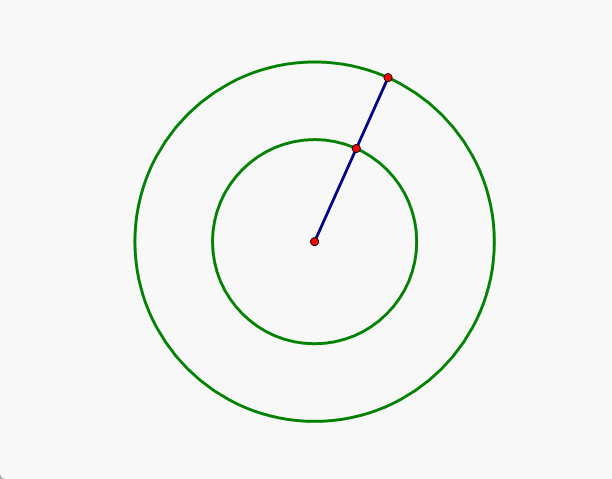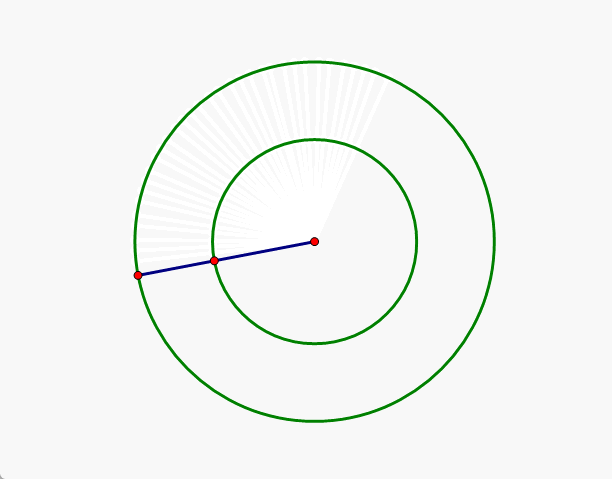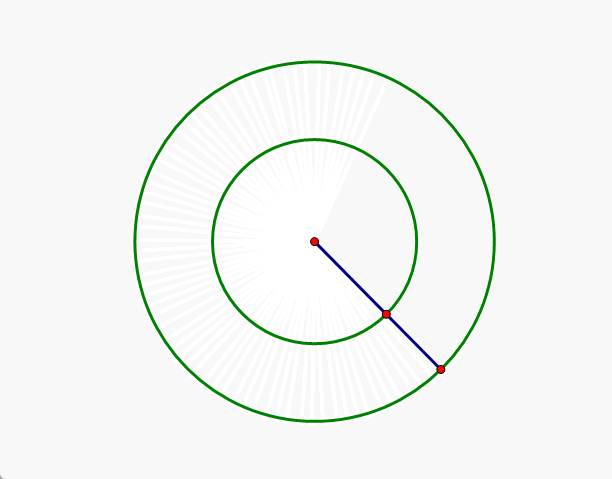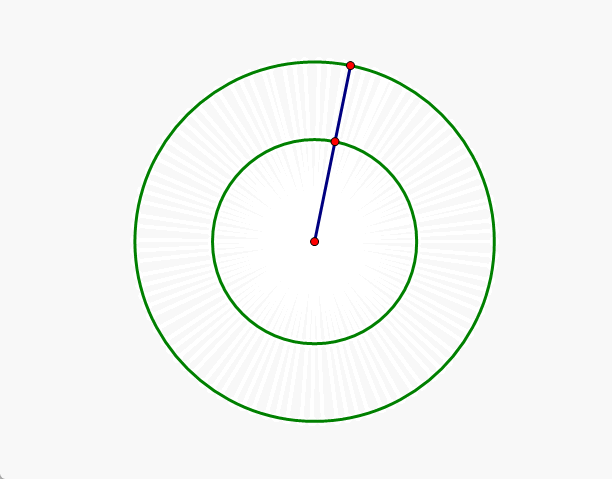
解析:由上面的动画可以看出,大圆上的任意一个点和小圆上的任意一个点之间是一一对应的,故两个同心圆上的点是一样多的。
正半轴只是数轴这个整体的一部分,难道她[部分]上面的点还会比整体多吗,打死我都不信,不过不信由不得你。
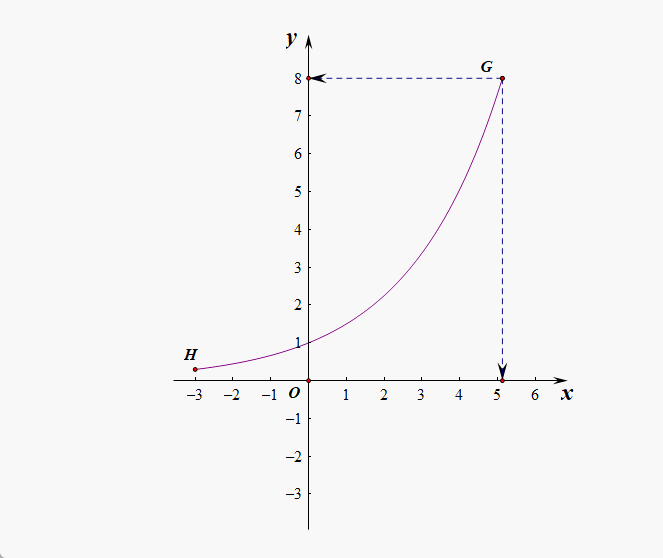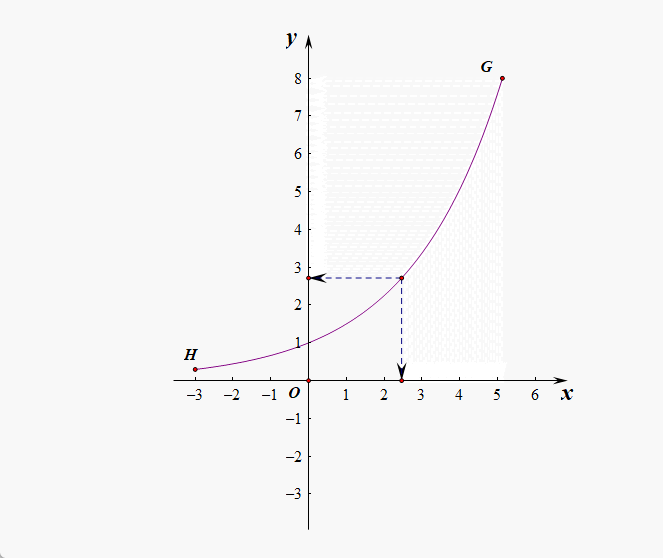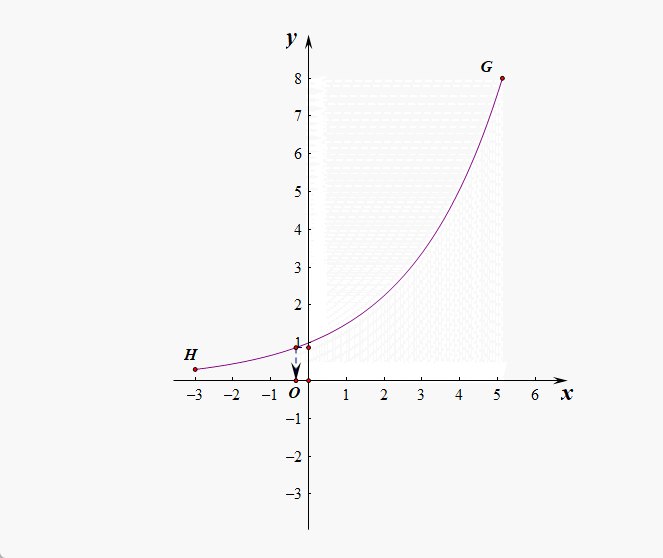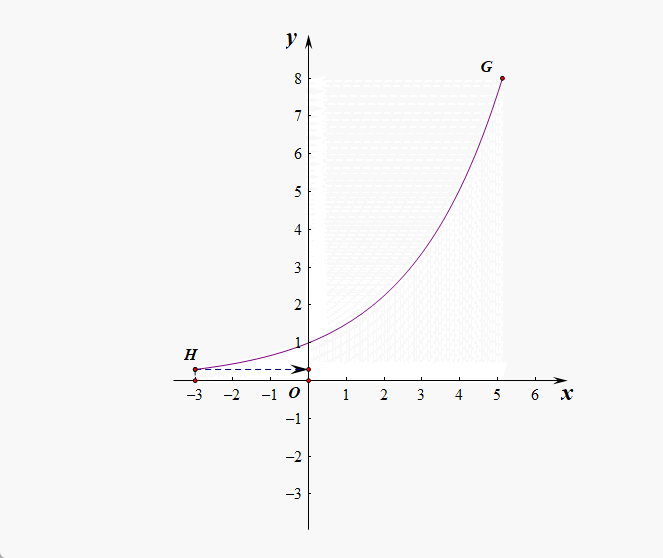
解析:以指数函数为依托,我们发现数轴 \(x\)上 的任意一个点和数轴 \(y\) 正半轴上的任意一个点之间是一一对应的,故数轴上的点和正半轴上的点是一样多的。所以教材上说,指数函数是实数集到正实数集的一一映射,同理,对数函数是正实数集到实数集的一一映射。